[SinGuLaRiTy] NOIP模拟赛(TSY)-Day 1

游戏 (game)

题目描述

A和B在玩游戏。桌子上有n个格子，其中一些格子放有棋子‘x’，空格子用‘o’表示。A和B轮流进行以下操作中的任何一种。
1>当某一个棋子右边有空格时，将该棋子向右移动一位。
ooxoo -> oooxo
2>当某一个棋子右边恰好是连续的两个棋子时，将该棋子直接跳过连续的两个棋子。
ooxxxoo -> oooxxxo
当棋子到达终点(最右端的格子)时，棋子将消失。当某一方不能移动时，这方输。A先走。请问A是否必胜？

输入

多组测试数据。
对于每一组测试数据：
第一行输入一个整数n，表示格子数量。
第二行输入长度为n的‘x’‘o’串。

输出

对于每一组测试数据，输出一行“YES”或者“NO”。

样例数据

样例输入	样例输出
4 ooxo 4 xxxo 5 oxxxo	YES NO NO

<数据范围>

对于30%的数据，n<=20。
对于100%的数据，n<=10^6 ，测试数据组数 T<=5。

解析

这道题其实考点是博弈论(还不了解博弈论?阅读一下这些论文吧。[点击下载]) ，不过由于策略比较简单，可以通过找规律来得到答案。

考虑所有棋子到终点的距离和sum，观察无论哪一种操作都恰好改变了sum的奇偶性。若sum为奇数，则A必胜；否则A必败。

时间复杂度：O(n)。

Code

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

#define N 1000005

#define ll long long

char S[N];

int t,n;

ll k;

int main()

{

    while(scanf("%d",&n)==)

    {

        scanf("%s",S+);

        k=;

        for(int i=;i<=n;i++)

        if(S[i]=='x')

            k+=n-i;

        if(k&)

        printf("YES\n");

        else

        printf("NO\n");

    }

    return ;

}

轰炸 (bomb)

题目描述

A国和B国开战。B国国王痴迷于树，所以B国的城市道路是一棵树的形状。A国情报局通过B国地下组织获取了该消息……给力的地下党还窃取了B国每一个城市的火药储备量m[i]，即轰炸城市i可以同时炸掉距离城市i在m[i]之内的其他城市。
由于A国国力有限，A国情报局局长想知道至少需要炸几次才能把B国所有城市都炸掉……

输入

第一行输入一个整数n，表示B国的城市数量。
第二行输入n个整数，第i个整数m[i]表示城市i的火药储备量。
接下来的n-1行，每一行输入两个整数u、v，表示一条连接城市u、v长度为1的城市道路。

输出

输出一行一个整数，即最少轰炸次数。

样例数据

样例输入	样例输出
5 1 1 1 1 1 1 2 2 3 3 4 4 5	2

<数据范围>

对于10%的数据，n<=10 。
对于30%的数据，n<=1000 。
对于100%的数据，n<=10^5 , m[i]<=100 。

解析

一看这道题，就感觉有点像战略游戏这道题，于是就想到了用树形DP。

好吧，这就是一道典型的树形DP。

令f[u][i]表示以u为根的子树被完全破坏，同时还能向上延伸i的最小值。

令g[u][i]表示以u为根的子树未被完全破坏，还应向下延伸i的最小值。

转移方程式：

1.不轰炸u节点

2.轰炸u节点

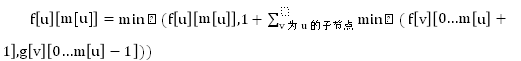
很显然直接这样做是会TLE的。

令minf[u][i]表示，同理ming[u][i]表示

再用s1[u][i]表示

s2[u][i]表示

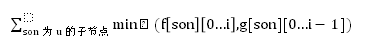
那么上述转移方程式可以写成：

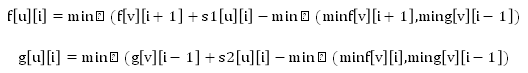
这样时间复杂度为O(100n)。

Code

#include<cstdio>

#include<iostream>

#include<cstring>

#include<cmath>

#define MAXN 100010

using namespace std;

char word;

void Read(int &t)

{

    t=;

    do word=getchar();while(word<''||word>'');

    do{t=t*+word-'';word=getchar();}while(word>=''&&word<='');

}

struct node

{

    int v;

    node *next;

}edge[MAXN*],*adj[MAXN],*tmp=edge;

int n, mx, m[MAXN];

int f[MAXN][],minf[MAXN][],g[MAXN][],ming[MAXN][],s1[MAXN][],s2[MAXN][];

inline void add(int u,int v)

{

    tmp->v=v;

    tmp->next=adj[u];

    adj[u]=tmp;

    ++tmp;

    tmp->v=u;

    tmp->next=adj[v];

    adj[v]=tmp;

    ++tmp;

}

void dp(int u,int fa)

{

    int v,i;

    for(node *p=adj[u];p;p=p->next)

        if((v=p->v)!=fa)

        {

            dp(v,u);

            s1[u][]+=minf[v][],s2[u][]+=minf[v][];

            for(i=;i<=mx;++i)

                s1[u][i]+=min(minf[v][i+],ming[v][i-]),s2[u][i]+=min(ming[v][i-],minf[v][i]);

        }

    for(i=mx+;i>=;--i)

        f[u][i]=g[u][i]=minf[u][i]=ming[u][i]=n;

    g[u][]=s2[u][];

    for(node *p=adj[u];p;p=p->next)

        if((v=p->v)!=fa)

        {

            f[u][]=min(f[u][],f[v][]+s1[u][]-minf[v][]);

            for(i=;i<=mx;++i)

            {

                f[u][i]=min(f[u][i],f[v][i+]+s1[u][i]-min(minf[v][i+],ming[v][i-]));

                g[u][i]=min(g[u][i],g[v][i-]+s2[u][i]-min(ming[v][i-],minf[v][i]));

            }

        }

    f[u][m[u]]=min(f[u][m[u]],s1[u][m[u]]+);

    minf[u][]=f[u][],ming[u][]=g[u][];

    for(i=;i<=mx+;++i)

        minf[u][i]=min(f[u][i],minf[u][i-]),ming[u][i]=min(g[u][i],ming[u][i-]);

}

int main()

{

    scanf("%d",&n);

    for(int i=;i<=n;++i)

        Read(m[i]),mx=max(mx,m[i]);

    for(int i=,u,v;i<n;++i)

        Read(u),Read(v),add(u,v);

    dp(,);

    printf("%d",minf[][mx]);

    return ;

}

统计 (count)

题目描述

定义一个整数集合S，S中的元素满足在十进制表示下只有5和7，例如5、7、57、75。
对于一个有n个元素的数列{a}进行以下两种操作：
操作一：add l r v，表示对于数列中加上v。
操作二：query l r，表示询问数列中有多少个 i∈[l,r]满足 ai∈S。

输入

第一行输入两个整数n、m，分别表示数列长度和操作次数。
第二行输入n个整数，表示这个数列。
接下来的m行，每一行输入一个操作，操作格式如上。

输出

对于每一个询问操作输出一行一个整数。

样例数据

样例输入	样例输出
10 5 1 5 7 2 5 75 8 7 9 57 query 2 7 add 1 5 2 query 1 5 add 3 8 -1 query 1 10	4 2 3

<数据范围>

对于100%的数据，n,m<=10^5，ai在任何时刻都满足ai∈[1,10000]。

解析

令K表示在10000以内S集合的元素个数，K=30。

把序列划分成长度为B的若干块。对于一个块，用cnt[i]表示i在块中的个数，同时维护一个加法标记。

接下来考虑如何处理这两种操作：

Add l r：对于块外的元素，暴力修改，时间复杂度O(B)。对于连续的块，修改标记即可,时间复杂度O(n/B)。

Query l r v：对于块外的元素，标记下传暴力查询，时间复杂度O(B)。对于连续的块，假设已经打上了Δx的标记，就对于每一个L∈S，统计块中有多少个L-Δx，时间复杂度O(n*K/B)。

总时间复杂度：O(m*(B+n*K/B))。由耐克函数的相关性质可得，当时B=sqrt(n*K/B)，时间复杂度最小。

Code

#include<iostream>

#include<cstdio>

#include<cmath>

#define MAXN 100005

using namespace std;

char word,s[];

bool ff;

void Read(int &t)

{

    t=,ff=;

    do{word=getchar();if(word=='-')ff=;}while(word<''||word>'');

    do{t=t*+word-'';word=getchar();}while(word>=''&&word<='');

    if(ff)t=-t;

}

int n,m,cnt,num[MAXN],pos[MAXN],pos2[MAXN];

const int a[]={,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,};

bool F[];

struct block

{

    int num[], len, flag;

    int cnt[];

    inline void add(int a)

    {

        ++cnt[a];

        num[++len]=a;

    }

    inline void putdown()

    {

        if(flag)

        {

            for(int i=;i<=len;++i)

            {

                --cnt[num[i]];

                num[i]+=flag;

                ++cnt[num[i]];

            }

            flag=;

        }

    }

    inline void modify(int l,int r,int v)

    {

        if(l==&&r==len)

        {

            flag+=v;

            return;

        }

        putdown();

        for(int i=l;i<=r;++i)

        {

            --cnt[num[i]];

            num[i]+=v;

            ++cnt[num[i]];

        }

    }

    inline int query()

    {

        int ans=;

        for(int i=;i<=;++i)

            if(a[i]-flag<=&&a[i]-flag>=)

                ans+=cnt[a[i]-flag];

        return ans;

    }

    inline int query(int l,int r)

    {

        if(l==&&r==len)

            return query();

        putdown();

        int ans=;

        for(int i=l;i<=r;++i)

            if(F[num[i]])

                ++ans;

        return ans;

    }

}b[];

inline void build()

{

    int l=(int)sqrt(n*+0.5);

    cnt=;

    for(int i=;i<=n;++i)

    {

        if(b[cnt].len==l)

            ++cnt;

        b[cnt].add(num[i]);

        pos[i]=cnt, pos2[i]=b[cnt].len;

    }

}

inline void add(int l,int r,int v)

{

    int L=pos[l], R=pos[r];

    if(L==R)

    {

        b[L].modify(pos2[l],pos2[r],v);

        return;

    }

    for(int i=L+;i<R;++i)

        b[i].flag+=v;

    b[L].modify(pos2[l],b[L].len,v);

    b[R].modify(,pos2[r],v);

}

inline int query(int l,int r)

{

    int L=pos[l],R=pos[r];

    if(L==R)

        return b[L].query(pos2[l],pos2[r]);

    int ans=b[L].query(pos2[l],b[L].len)+b[R].query(,pos2[r]);

    for(int i=L+;i<R;++i)

        ans+=b[i].query();

    return ans;

}

int main()

{

    for(int i=;i<=;++i)

        F[a[i]]=;

    Read(n),Read(m);

    for(int i=;i<=n;++i)

        Read(num[i]);

    build();

    int l,r,v;

    while(m--)

    {

        scanf("%s",s);

        Read(l),Read(r);

        if(s[]=='a')

        {

            Read(v);

            add(l,r,v);

        }

        else

            printf("%d\n",query(l,r));

    }

    return ;

}

Time: 2017-07-27