冷扑大师AI简史：你用德扑来游戏，人家用来发Science

前言

人类又输了......

创新工场组织的一场“人工智能和顶尖牌手巅峰表演赛中”，机器人AI冷扑大师赢了人类代表队龙之队 792327 记分牌，最后 200 万奖励归机器人所有。

在围棋项目上人类的一票大师已经被 AlphaGo 虐得得不行。然而这还不算完，最近有在朋友圈里看到不少 “AI 首次在德州扑克战胜人类职业玩家，新算法让机器拥有直觉 ” 这类新闻。

所以简单给大家介绍下本次获胜的 Poker AI Libratus，以下解读来源于胡开亮同学的知乎回答。

CMU的Libratu原理，也是发过Science论文的内容

http://www.cs.cmu.edu/~sandholm/Solving%20games.Science-2015.pdf

首先跟大家简单介绍下纳什均衡的概念--- 纳什均衡是指一个策略组，任何玩家都无法通过单方面的改变策略来增加收益。纳什均衡策略组中的每个玩家的策略都是对策略组中其他策略的最佳反应。纳什均衡策略组很重要，因其在两人零和博弈中有额外的属性。在两人零和博弈中,若某玩家从纳什均衡策略组中选中一个策略，其他玩家改变策略不会获得更大的收益。而在大部分Poker AI 中都是希望求解出来的策略组跟真正的纳什均衡足够的近记为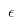。所以这样策略组的 exploitability 是足够小的，在假定对手有足够能力的来利用我的缺点（given sufficient exploitative power）的情况下，我的策略也是可行的。

介绍完纳什均衡后，我们可能在想怎么求解德州扑克中的纳什均衡，接着介绍用来求解均衡的 CFR ( Counterfactual regret minimization ) 中文名字叫：虚拟遗憾最小化算法。 CFR 来源于 Regret matching 算法，然而 Regret Matching 算法只能适用于正则博弈中，对于德州扑克这类扩展式博弈中无法直接使用 Regret Matching , 通过定义 Counterfactual Value 在每一个 Information Set 上进行 Regret Matching 来减少每一个 Information Set 上的 Immediate Regert,而Immediate regret 的和是小于 external regret.而 external regret 跟 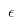- nash equilibrium 之间是有关系的，从而可以使用CFR来求解出纳什均衡解。但是 CFR 的空间复杂度为 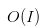,对于二人限制性的通过一些lossless abstraction 后就可以直接求解，对于二人非限制性（游戏空间大概为 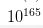)根本无法直接求解，故先用abstraction 然后再 CFR，大致的流程如下：

然而到了13年的时候 Sam ( Noam 的师兄，CMU 的 PHD ) 首次将 Endgame 残局的思想引入到了二人非限制性中来了上图的框架变成了如下图所示。

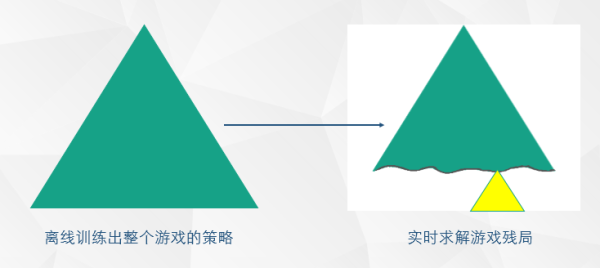
在 Endgame 中 agent 会根据玩家的在前几轮的 action，然后根据 action 所反映出来的手牌信息，对 Endgame 进行实时求解。实时计算需要具备强大的计算能力，这也是为什么Librauts在实际比赛中需要Brideges的原因。

上面就是 Libratus 的 part one- nash equilibrium approximation before the competition 和 part two-Endgame solving 的简单介绍，在实践中会用到很多 trick , 就拿 CFR 的改进来说--如何 Sample , Warm start, Pruning 以及Thresholding等等。在 Information Set abstraction 过程中如何选择特征进行聚类等等。

AI as a service，会让AI触手可及

其实除了 Libratu， Poker AI 领域还有 Alberta 大学的 DeepStack（https://arxiv.org/pdf/1701.01724v1.pdf）
当AI的来临变得不可避免的时候，开发者们需要思考如何让自己更快的拥抱AI时代。对于开发者而言，在深度学习领域常用的一些算法其实未来都可以通过腾讯云等公有云厂商的API方式进行调用。

例如把游戏或者 APP 服务器上的日志实时地同步到 COS 对象存储中，采用 DI-X 调度云端强大的 CPU 和 HPC 计算能力对用户行为或其他游戏日志进行数据清洗等预处理；接下来采用 Scale 等特征工程技术进行特征处理后的特征信息即可进入模型训练环节，训练完毕的模型将会被保存于 COS 对象存储中，以便于进行游戏流失率的预估。
游戏运营专家可以在游戏动态运营系统上，根据游戏流失率的预估结果选择策略以进行低活跃用户召回、用户流失原因分析、推广活动效果评估等动态运营。

小结：

人工智能处理人机对弈的信息模式可大致分为完美信息、不完美信息两类，大致对应两类博弈：围棋 vs 扑克

在这两个领域，人类都已经输给了人工智能，对于未来的开发者而言，拥抱而非排斥 AI 更为现实，而云计算会把 AI 的能力变得像水和电一样，更加触手可及。

此文已由作者授权腾讯云技术社区发布，转载请注明文章出处