A B-tree index can be used for column comparisons in expressions that use the =, >, >=, <, <=, or BETWEEN operators.

总结：

1、

一个算法由控制结构（顺序、分支和循环3种）和原操作（指固有数据类型的操作）构成的，则算法时间取决于两者的综合效果。

2、

N*N矩阵乘法算法

时间复杂度T(n)=O(n^3)

for(i=1;i<=n;i++)
　　for(j=1;j<=n;j++)
　　　　c[i][j]=0
　　　　for(k=1;k<=n;k++)
　　　　　　c[i][j]+=a[i][k]*b[k][j]

O(f(n))形式定义：

若f（n）是正整数n的一个函数，则O(f(n))表示

存在一个正常数M，使得当n>=n0时都满足O(f(n)<=M*f(n)

3、

常量阶 线性阶 平方阶 O(1) O(n) O(n^2)

对数阶指数阶 O(logN) O(2^n)

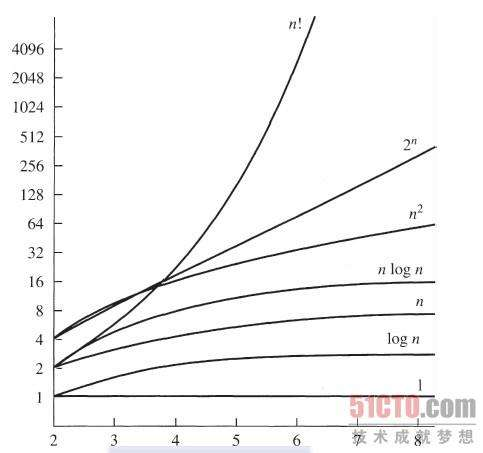
时间复杂度计算

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/two-sum

class Solution:
    def twoSum(self, nums, target):
        c = len(nums)
        for i in range(0, c, 1):
            if target - nums[i] in nums[i + 1:]:
                return [i, i + 1 + nums[i + 1:].index(target - nums[i])]

class Solution:
    def twoSum(self, nums, target):
        hashmap = {}
        for index, num in enumerate(nums):
            another_num = target - num
            if another_num in hashmap:
                return [index, hashmap[another_num]]
            hashmap[num] = index
        return None

O(n^2)

O(n)