机器学习-线性分类-SVM支持向量机算法-12

1. 铺垫感知器算法模型
2. SVM 算法思想
3. 硬分割SVM总结

支持向量机(Support Vector Machine, SVM)本身是一个二元分类算法，是对感知器算法模型的一种扩展。

1. 铺垫感知器算法模型

什么是感知器算法模型？

感知器算法是最古老的分类算法之一，原理比较简单，不过模型的分类泛化能力比较弱，不过感知器模型是SVM、神经网络、深度学习等算法的基础。

感知器的思想很简单：在任意空间中，感知器模型寻找的就是一个超平面，能够把所有的二元类别分割开。感知器模型的前提是：数据是线性可分的。

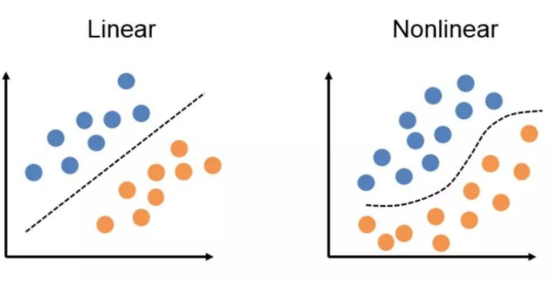
找到这样的参数θ：让一个类别的样本满足：θx>0 ；另外一个类别的满足：θx<0

正确分类：yθx>0，

错误分类：yθx<0

所以我们可以定义我们的损失函数为：期望使分类错误的所有样本到超平面的距离之和最小。

参考下逻辑回归：

逻辑回归的几何意义，又何尝不是向量空间找到一个超平面，超平面一侧的点计算分数结果为负，另一侧结果分数为正（感知器算法模型），只不过最后不直接看sign符号，而是根据sigmoid函数将分数映射到0-1之间通过最大似然来赋予概率意义。

感知器算法模型：向量空间找到一个超平面，超平面一侧的点计算分数结果为负，另一侧结果分数为正， sign(θx)

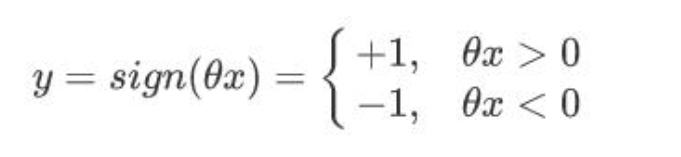
几何距离：

高维空间中，任意一个点 X0 其对应标签为 y0，到某平面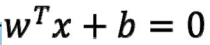的距离

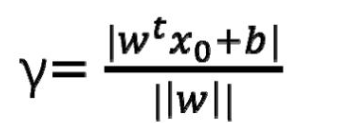
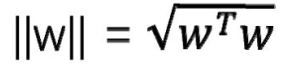
对于那些正确分类的点，将距离表示为：

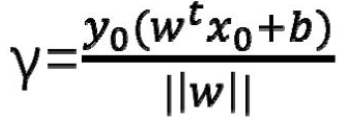
分子部分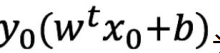

称为函数距离

损失函，对于分类错误的点，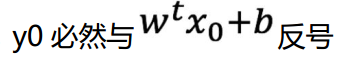

要想使得损失函数是大于 0 的，所以分类错误的点距离在前面加个负号

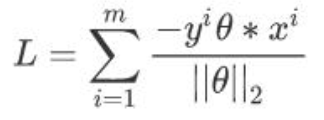
当分子扩大 N 倍的时候，分母也会随之扩大，也就是说分子和分母之间存在倍数关系，所以可以固定分子或者分母为 1，我们固定分母为1；

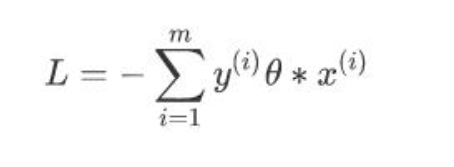
不过由于这里的 m 是分类错误的样本点集合，不是固定的，所以我们不能使用批量梯度下降法(BGD)求解

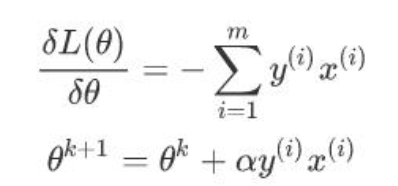
2. SVM 算法思想

SVM 也是通过寻找超平面，用于解决二分类问题的分类算法

超平面一侧的点计算分数结果为负是负例，另一侧结果分数为正是正例

与感知机相同，通过 sign 给出预测标签，正例为+1，负例为-1，模型判别式同样：

不同点：

感知器是通过判断错误的点寻找超平面

逻辑回归是通过输出概率的最大似然来求解参数

SVM是通过寻找支撑向量来寻找超平面

通过寻找支撑向量来寻找超平面？？？什么意思？不太懂？后文还回继续讲解

感知器算法模型寻找超平面将正例负例区分开来即可所以新来的样本泛华能力表现一般。

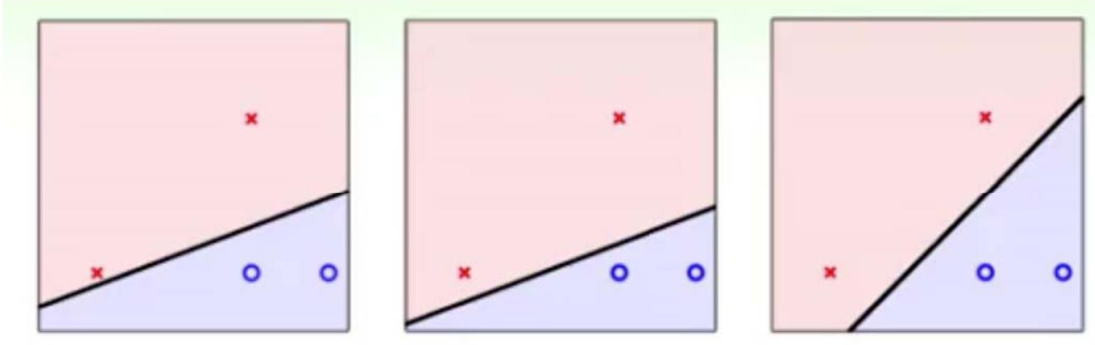
这些分界线哪个更好，这便是 SVM 要解决的问题

实际上离超平面足够远的点基本上都是被正确分类的，

所以这个是没有意义的；反而比较关心那些离超平面很近的点，这些点比较容易分错

假设未来拿到的数据含有一部分噪声，那么不同的超平面对于噪声的容忍度是不同的，

最右边的线是最 robust 的。

换一种角度考虑，找到最胖的超平面--换句话说就是：只要让离超平面比较近的点尽可能的远离这个超平面，那么我们的模型分类

效果应该就会比较不错。离超平面比较近的点就是需要寻找的支撑向量

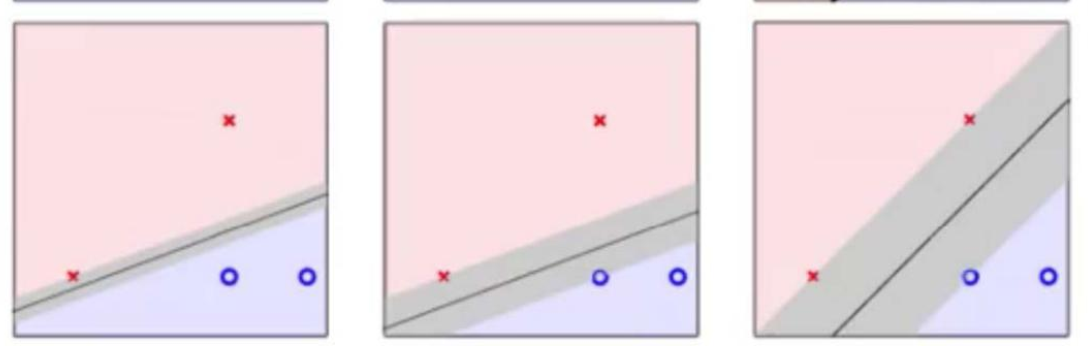
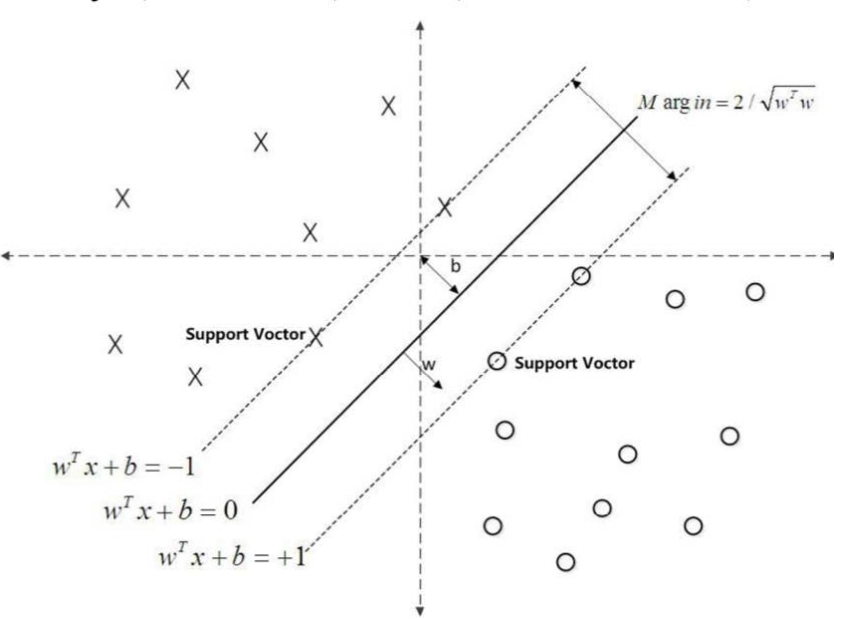
距离超平面最近的且满足一定条件的几个训练样本点被称为支持向量

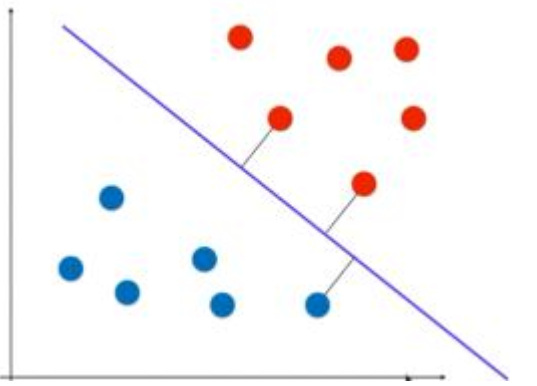
一句话总结：SVM 尝试找到一个决策边界,距离两个类别最近的样本最远，这样的超平面则是符合条件的超平面！！

需要找到一个超平面：

能够完美分类正负例
距离最近的点越远越好

正确分类的平面中，距离越近的点越远越好

也就是说，找到一组最好的 w 和 b 固定一个超平面，使这个超平面在能完美区分正负例的

基础上，距离最近的点间隔最大

转化成数学描述：

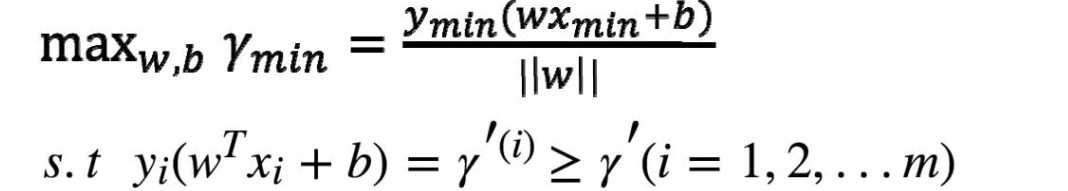
一个超平面对应无数个 w,b，只要找到其中任意一个 w 符合条件的 w 就可以了选择最好求的

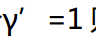
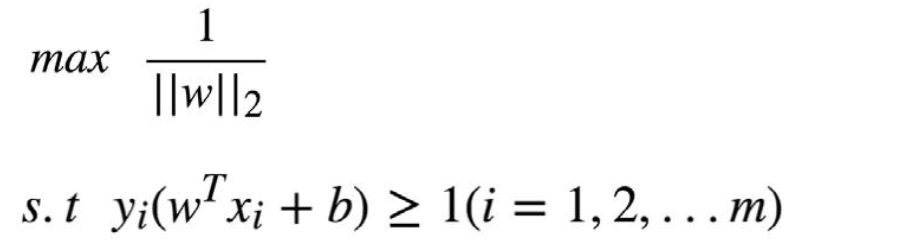
等价于：

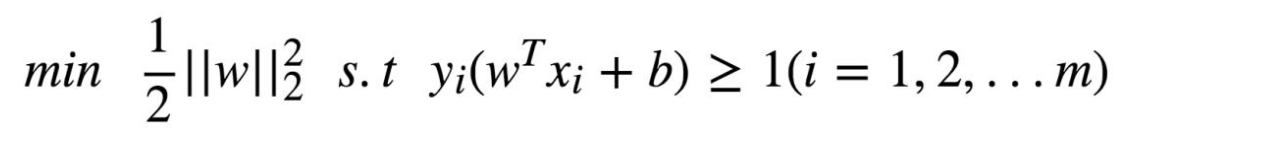
本质上这里不就是L2范数最小

铺垫拉格朗日函数

原始问题：

约束条件表述为 k 个不等式约束条件，和 L 个等式约束条件

转化成拉格朗日函数：

其中 ci 是第 i 个不等式约束函数（需要整理），bj 是第 j 个等式约束函数αi 和βi 是拉格朗日乘子

原始问题：

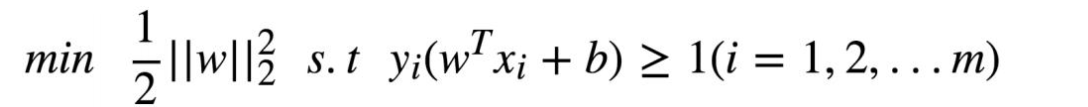
构建拉个朗日函数：

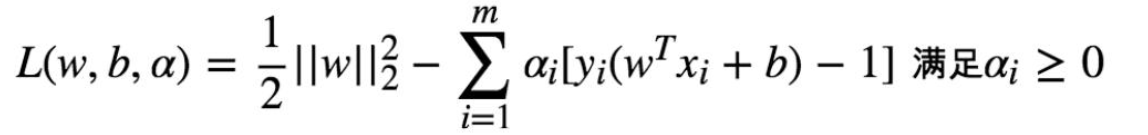
对偶原理：

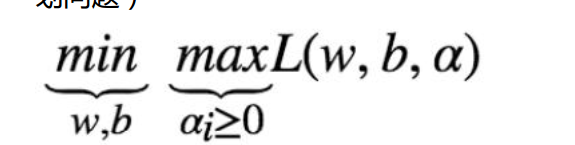
转化成：

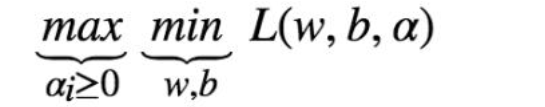
下面就开始求解对偶函数的第一步

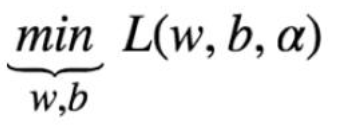
拉格朗日函数分别求 w 和 b 的偏导：

将 w 反代回原来的拉格朗日函数中就可

以进行第二步求关于α的极大了

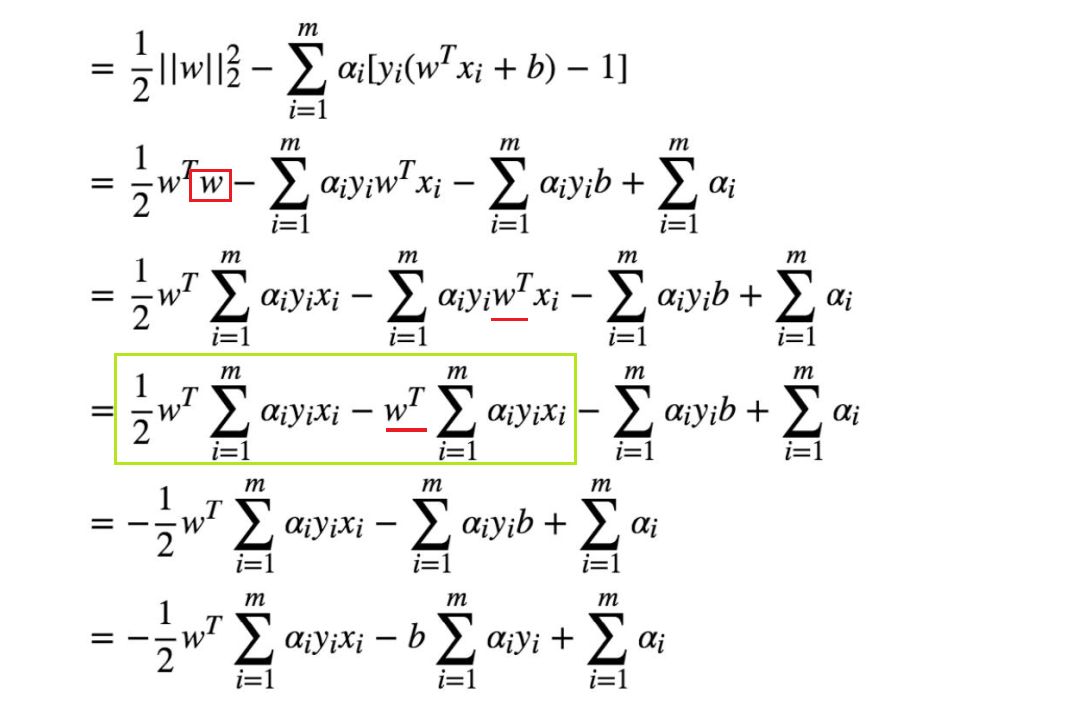
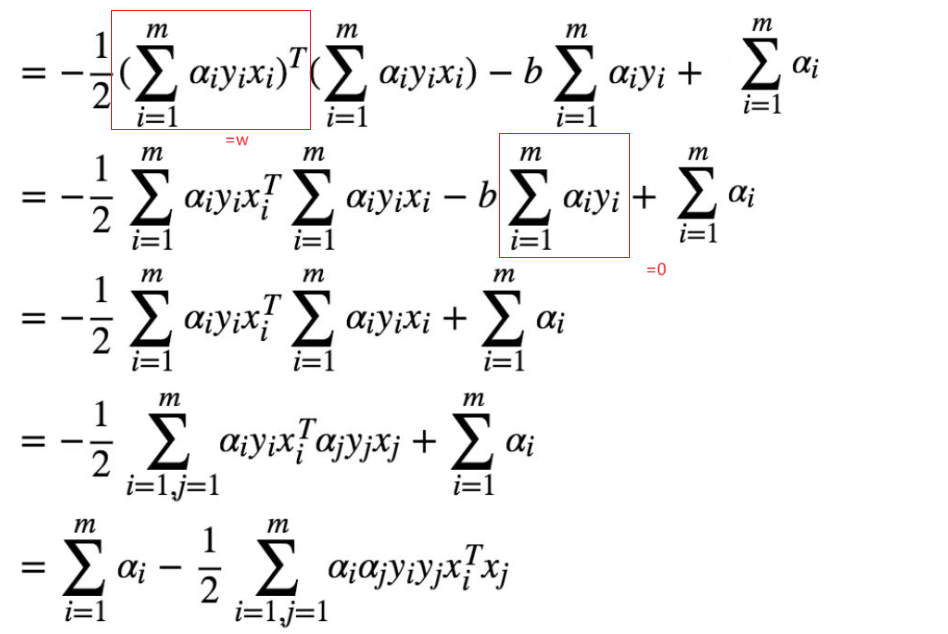
第二步对对偶函数的优化问题

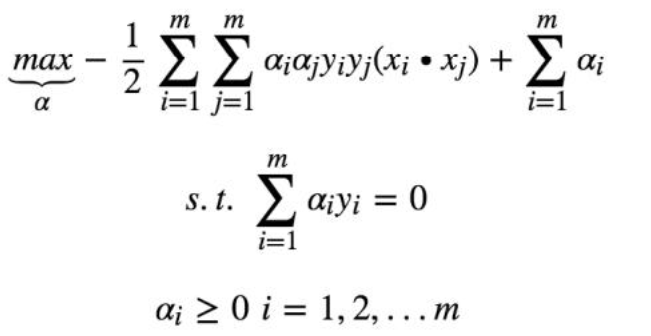
去掉负号转换为求极小问题

只要解决了这个问题，svm 的学习问题就完成了

通常使用 SMO 算法进行求解，可以求得一组α* 使得函数最优化

smo算法后面再讲，假设我们已经得到α*

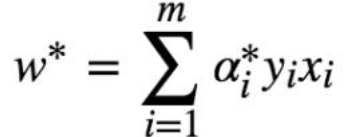
将xi yi带入就能求得w*

b*怎么求解？对于支持向量上的点满足：

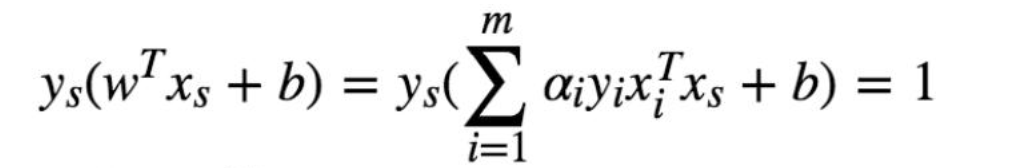
如何寻找支持向量？

ktt条件：

那么所有α>0 时后面一项需要=0 也就是

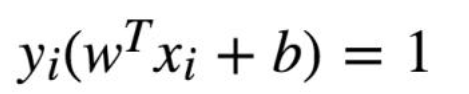支持向量

求 b 的过程：找到所有个支持向量带进去求出所有个 b，然后求平均这样我们就得到了分割超平面

这样我们就得到了分割超平面

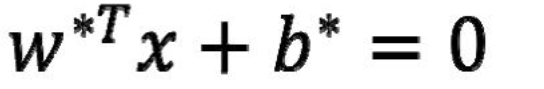
3. 硬分割SVM总结

1：目标：求得一组 w 和 b 使得分隔 margin 最大

2. 通过拉格朗日函数构造目标函数，问题由求得 n 个 w 和 1 个 b 转换为求得

m 个α

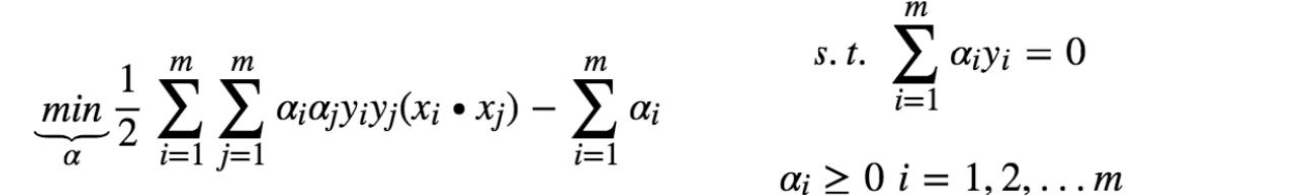
3. 利用 smo 算法求得 m 个α*

4. 利用求得的 m 个α求得 w和 b*