Metastability 亚稳态问题

亚稳态问题

各种跨时钟域的问题都会归结于亚稳态的问题,IP设计时钟域不超过两个,对于CDC设计要求不高;对于SoC设计来说,CDC处理十分重要

1.什么是亚稳态?

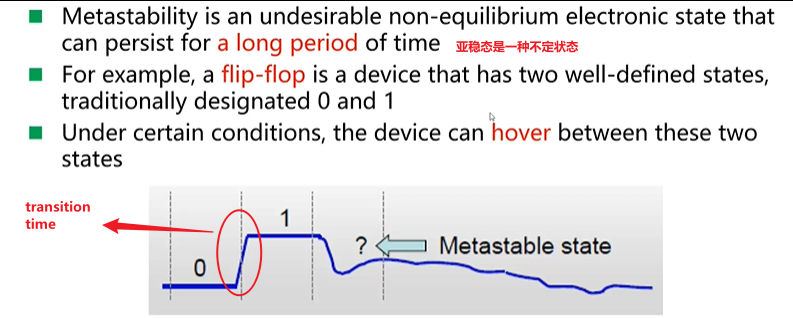
• transition time 是可以计算出来的值,与output load(输出负载),输出负载越大transition time 越大
• transition time 还与自身的驱动能力有关
• 不管怎样,transition time是电平能够正常进行0和1之间跳变的值,亚稳态则不相同,如果经过某些因素,输出状态会在0和1之间的状态震荡,并且经过很长一段时间之后,才能稳定到0和1之间的一个状态;并且这个状态可以作为门电路的输出,可能会驱动其他的门电路,会有较大的概率形成亚稳态
• 在一个节点形成亚稳态之后,会很快的进行扩散

2.亚稳态的危害

1. 亚稳态出现后进行传播
   
   
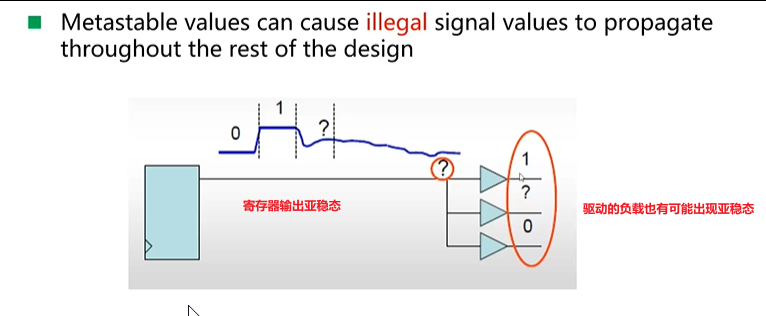
2. 亚稳态出现,稳定在一个值,这个0-1之间值,导致后续电路出现范围之外的值(无关项),会给电路带来未知的影响
   
   

2.1 亚稳态传播

对于寄存器来讲,时钟有效沿来临的时候,会采样D端值,将D端的值同步到Q端;时钟的有效沿来临之前一段时间,要保持信号稳定,称为setup time,在时钟有效沿来临之后的一段时间,信号依然要保持稳定,称为hold time,在setup time和hold time之间,输入发生了变化,中间的变化会形成不定态的传播,在采样的时候D端数据发生变化,就会形成亚稳态

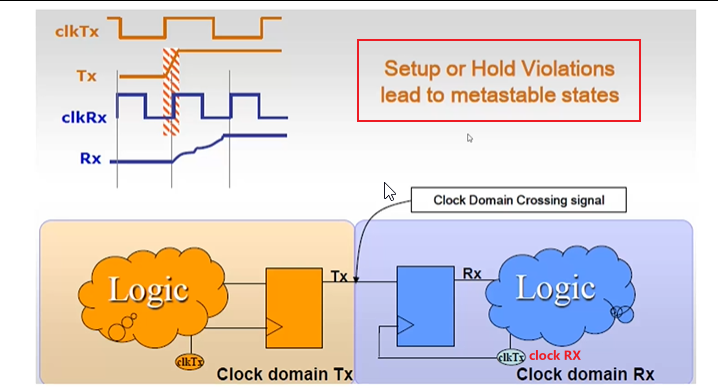
• 上图有两个时钟域,Tx输出的信号跳变的范围,遇到Rx时钟有效沿的变化,形成亚稳态
• 异步电路就是两个电路的时钟源是没有相位关系的,异步电路不能通过STA技术进行保证,需要进行跨时钟域的同步

3.亚稳态的状态

形成亚稳态之后,经过一定的震荡时间之后,亚稳态会回到0,1或一直震荡



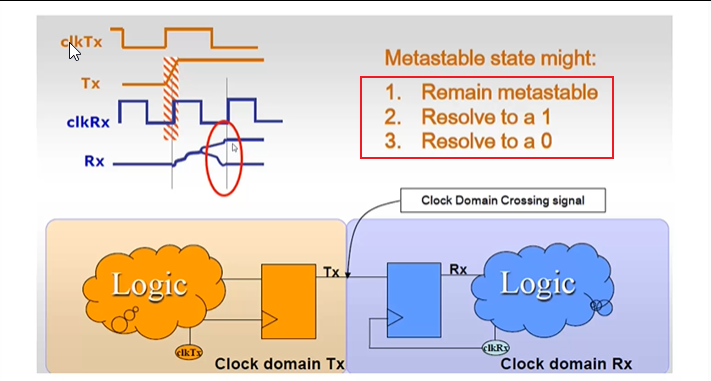
震荡时间与什么有关?

• Process - 制造工艺
• Temperature - 温度
• Voltage Samle - 电压
• Electromagnetic wave - 电磁波
• PVTE -- 延迟,布局布线.....都需要考虑的影响,主要是后端设计进行考虑

4.如何解决亚稳态

4.1 同步一位信号(同步器)

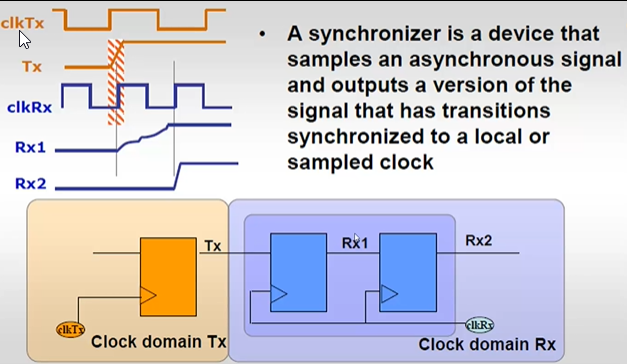
• 多打一拍 -- 使用两个寄存器
• Rx1没有发生亚稳态,Rx2也不会发生亚稳态;Rx1发生了亚稳态,那么在这个时钟周期之内有很大的可能性稳定到某一个值,那么再用一个寄存器Rx2多打一拍,则Rx2就是一个稳定的值
• 如果Rx1的震荡周期如果非常长,那么Rx2也有可能产生亚稳态,但是这种概率很小
• 1bit信号,使用两个寄存器打两拍的方式,可以解决亚稳态的问题,但是两个寄存器之间不能有任何的组合逻辑
• 一般公司中都会有这种跨时钟域处理方式的库文件,只要进行调用就行了,方便和后端进行同步,提高效率
  
  

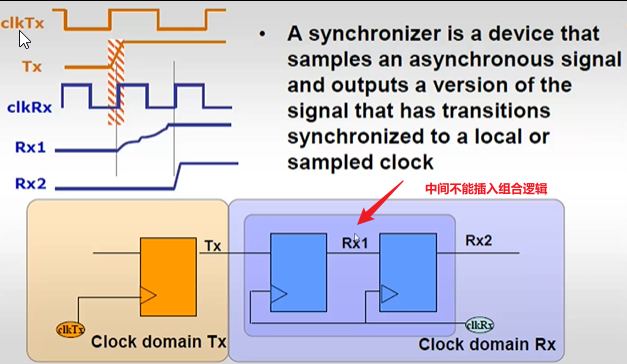
4.2 MTBS-Mean Time Between Failure

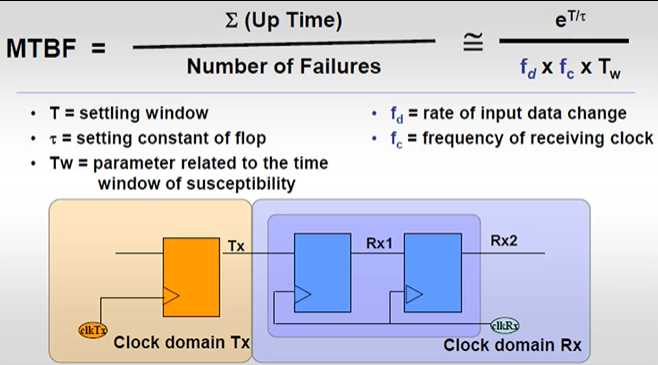
• 电路中出现两次亚稳态之间的时间间隔
• fd - 输入端数据变化的频率,信号输入的频率
• fc - 采样频率,有效沿来临的频率
• 输入信号频率越高,引起亚稳态失效的时间越短,亚稳态失效的频率越高
• 采样频率越快,采到在setup time和hold time之间信号的可能性越高,平均失效时间越短,在某个时间内亚稳态频率越快
  
  
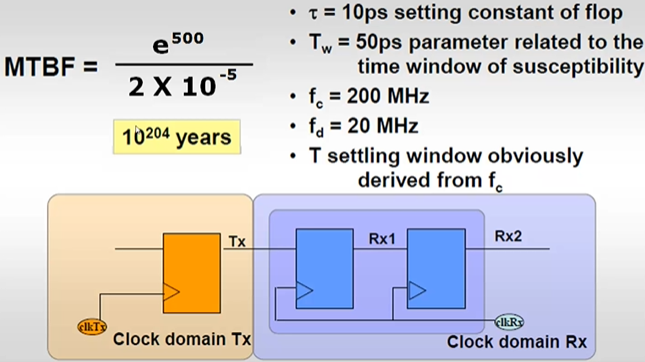
• MTBF - 数值非常大,说明两次亚稳态之间的时间非常长,认为不发生亚稳态
  
  使用三个寄存器处理1bit信号
  
  
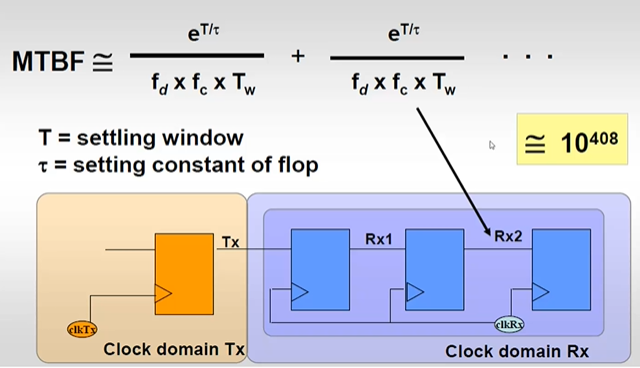
• 时钟信号高的时候,可以使用三个寄存器(同步器)处理

4.3 Synchronizer effect - latency uncertainty

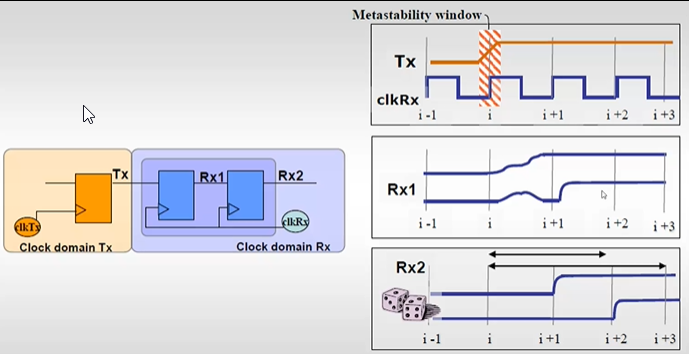
• Tx输入信号传递到Rx2的时间是不确定的,Rx1产生亚稳态,寄存器1,从clkRx上升沿开始采样,采集到的信号是亚稳态信号并传递给Rx1,Rx1在一个周期内,回归到1或0状态;当Rx1回归到1状态的时候,Rx2可以在i+1上升沿的时候采样到Rx1的信号;如果Rx1稳定到0状态,在i+1上升沿,Rx1会跳变为1,Rx2仍然为0,当i+2的上升沿的时候,Rx1保持为1,Rx2采样Rx1的信号变为1
• 由于亚稳态的存在,Tx信号传递到Rx2端的时间,可能是一个周期,也可能是两个周期,是不确定的
  
  RTL simulation does not model silicon behavior accurately
  
  
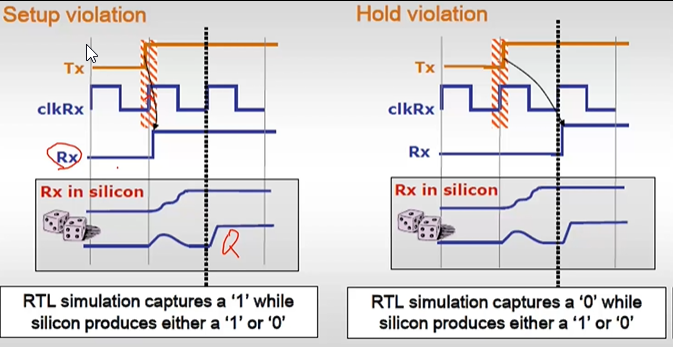
• 仿真工具是不会仿真出来亚稳态问题的,仿真器是非黑即白的
• 检测亚稳态问题的时候,通过后仿真的形式很难发现

4.4 同步多位信号

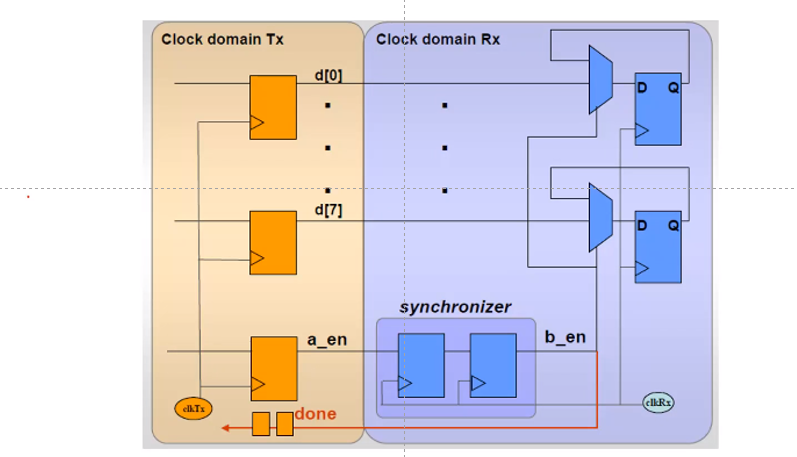
假设同步8bit信号经过时钟域

• 给每一位信号用二级同步器,是不可以的,因为亚稳态会导致latency uncertainty,不同位数据接收信号是不同步的
• 首先将enable信号进行同步,enable信号表示,8位信号都是ready的,a_en信号拉高,经过1-2个周期之后b_en得到a_en信号,b_en拉高,表示8位信号都是稳定的,可以进行采样,将8位信号采集到寄存器中
• 在信号同步完成之后需要给输入端一个信号,done信号,表示信号同步完成,可以进行下一组信号的传递,done信号也要经过两级同步器
• 使用异步FIFO处理多比特数据跨时钟域问题
• 使用握手机制处理跨时钟域问题

5.reconveragence problem - 重汇聚问题

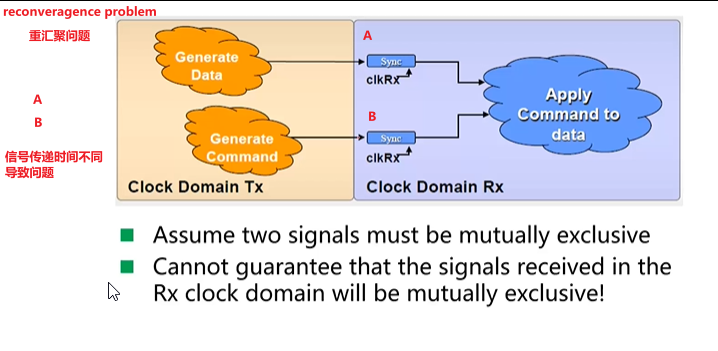
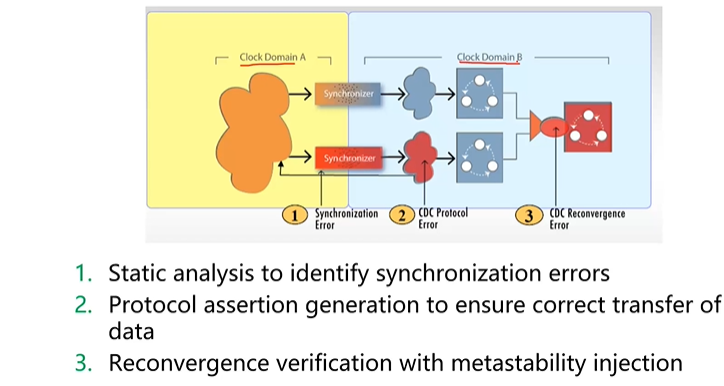
• 时钟域之间传递信号越少越好
• 时钟域同步机制越简单越好