Mesh快连

Mesh快连

一、名词解释

Mesh快连是一种由多个节点组成的网络系统，这些节点可以相互连接，形成一个“网状”的结构。

二、如何使用

有线Mesh：

网络拓扑：

设备版本：3.7.12企业版。

配置要求：从设备需恢复默认配置。

拓扑说明：设备接入电源，Q6000作为主设备通过LAN口连接从设备Q3000的WAN口，WEB页面操作在主设备均可完成，从设备无需进入WEB页面。

注意：mesh从设备默认绑定主设备的LAN1接口，且不支持配置，LAN1接口如果没有开启DHCP服务，mesh网络将无法自动获取IP地址

实现目的：通过Mesh功能实现无线信号的延续。

按照拓扑图连接线路后，在网络设置--Mesh快连，开启Mesh快连。

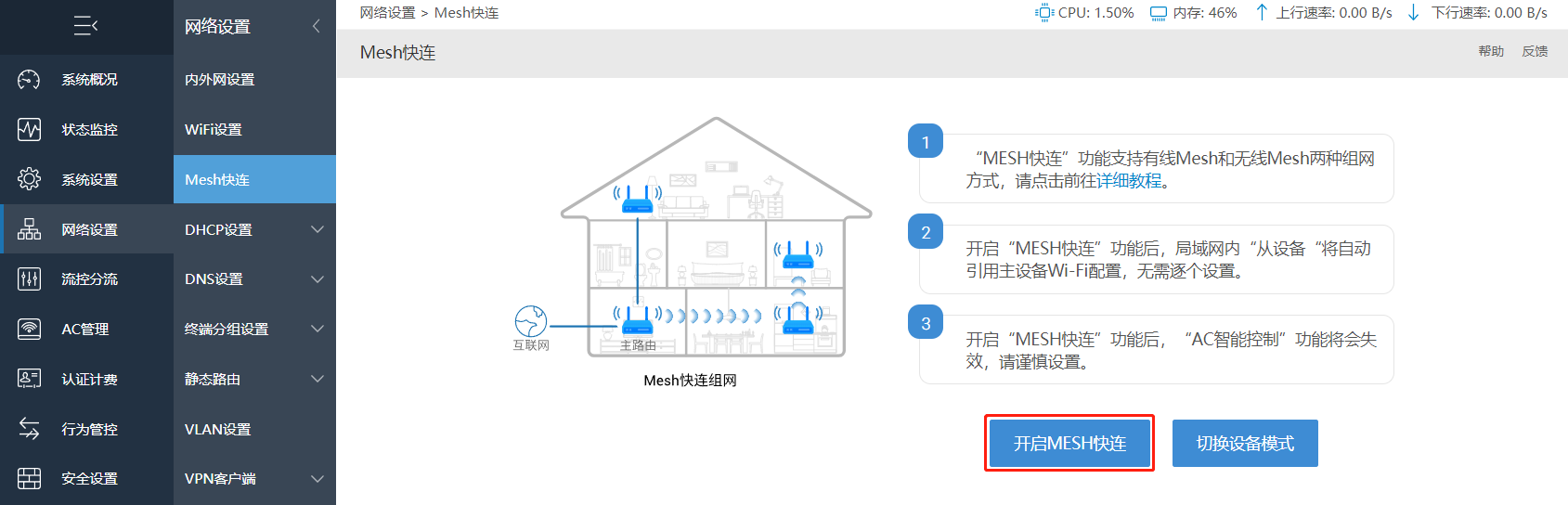
按照页面提示检查设备亮灯情况以及设备摆放位置。一切准备就绪后，点击开始配对。

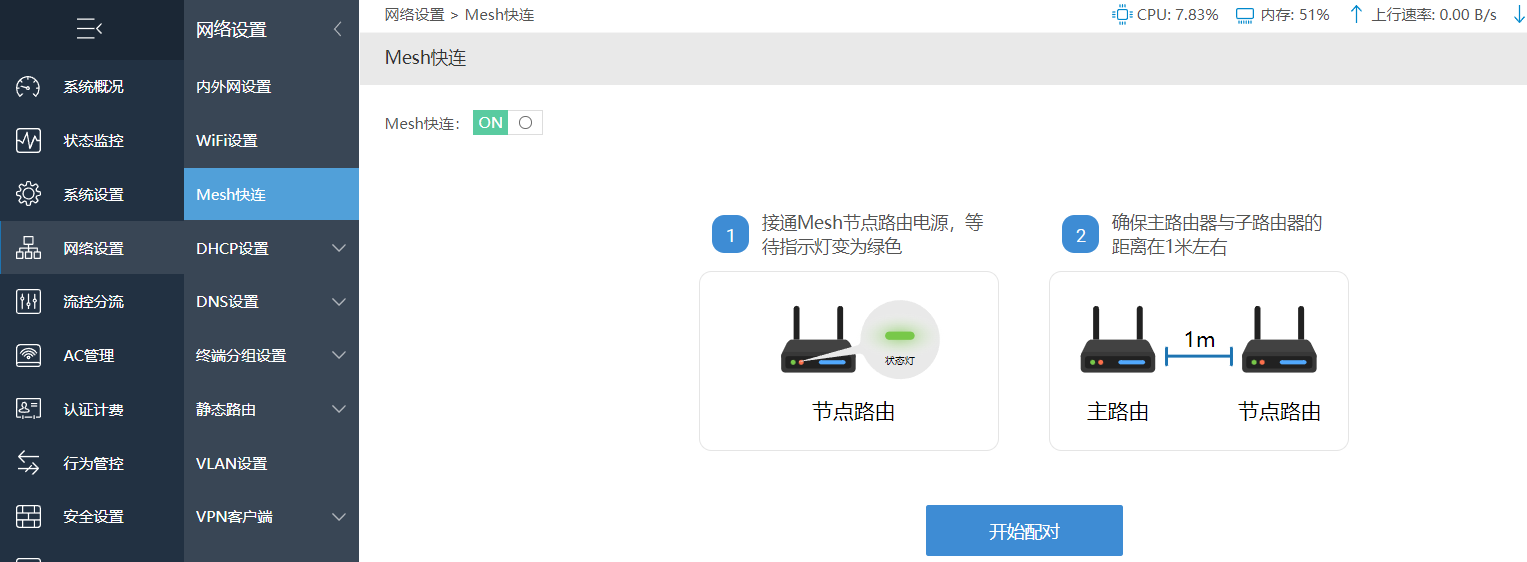
页面出现配对画面。

Mesh对接亮灯情况：

Q6000：

对接时：红绿灯交替闪烁。

对接成功：绿灯长亮。

Q3000：

对接时：彩灯交替闪烁，如对接时无灯闪烁，可按Mesh键3次。

对接成功：粉色灯长亮。

对接成功后设备灯显示效果：

配对时页面会显示网络中所有从设备MAC地址，MAC地址全面扫描完成后，点击停止配对。

配对成功后，在列表模式下，会显示配对的设备名称、MAC地址、有线速率、上联设备。如网络中有多个上联设备情况下，可点击操作处“首选上联设备”选择对应上联设备MAC信息。

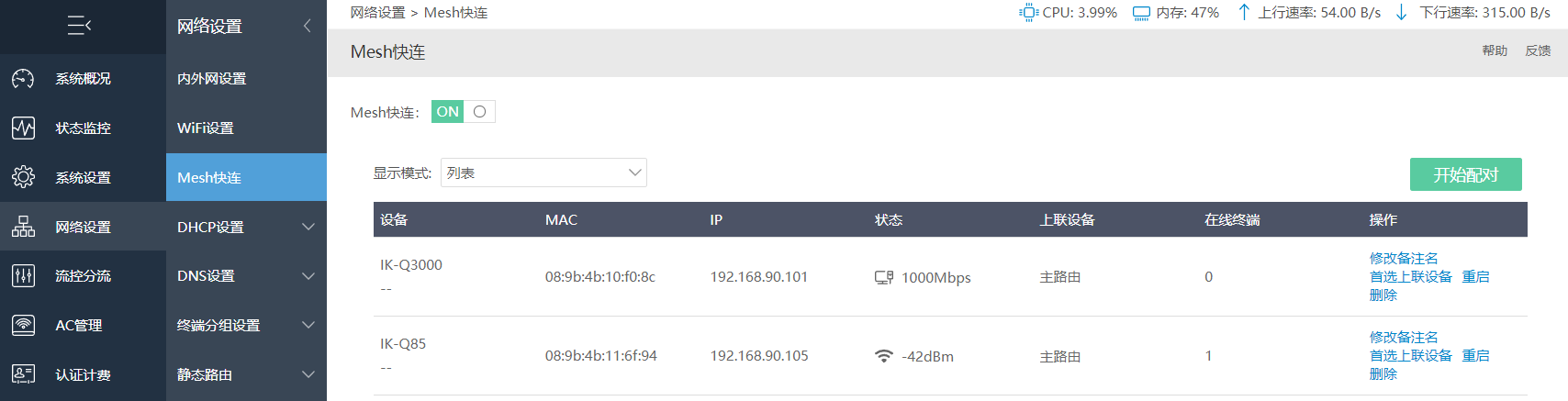
在显示模式中切换模式为”拓扑”，显示当前Mesh组网拓扑图。

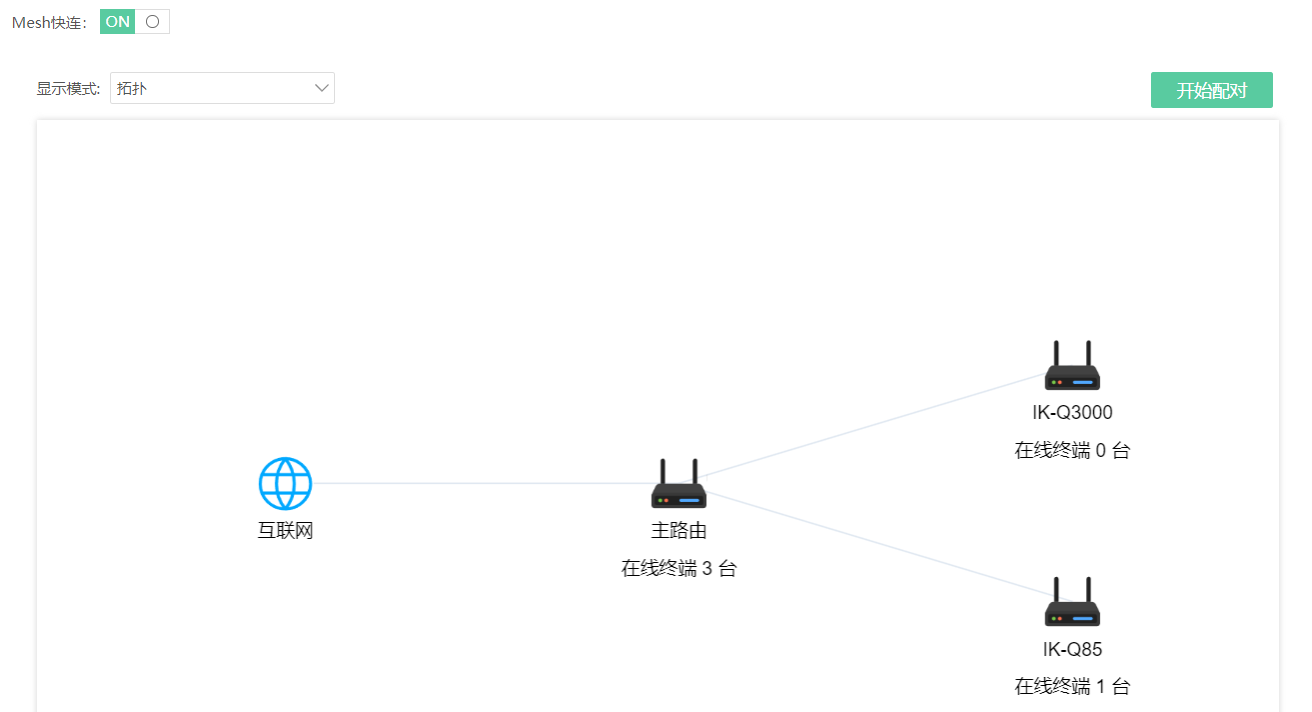
Mesh对接成功后设置无线名称，进行Mesh快连测试。

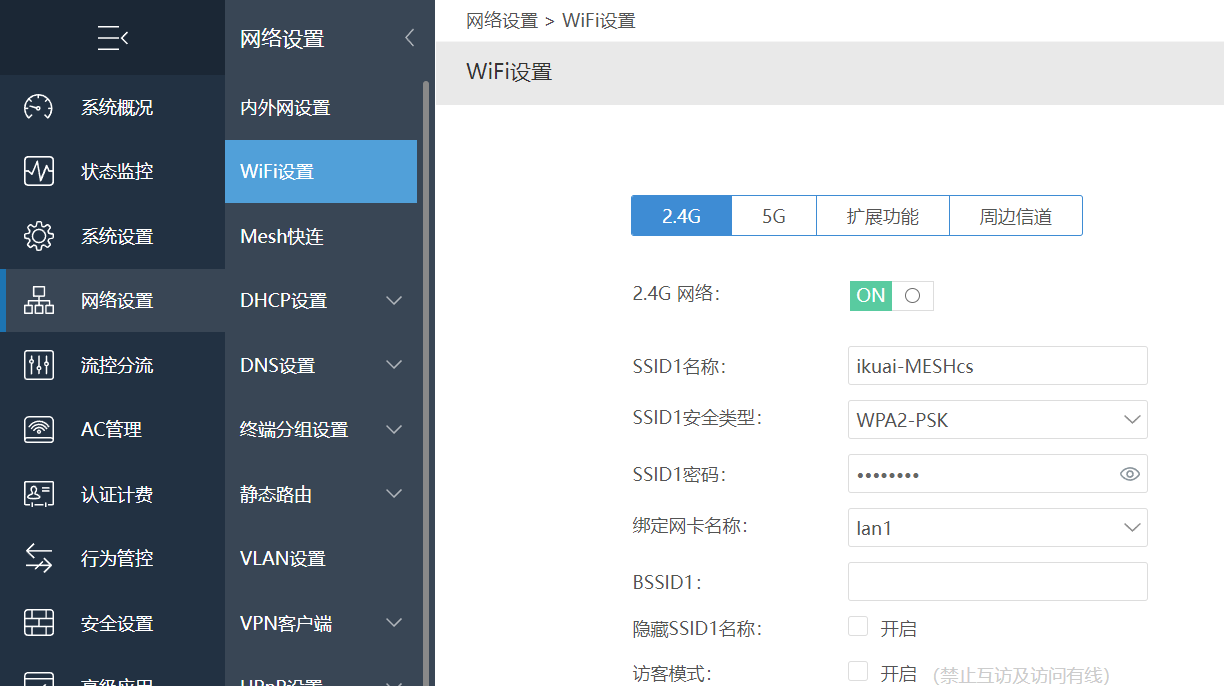
在AC管理--AP列表会显示Mesh设备。

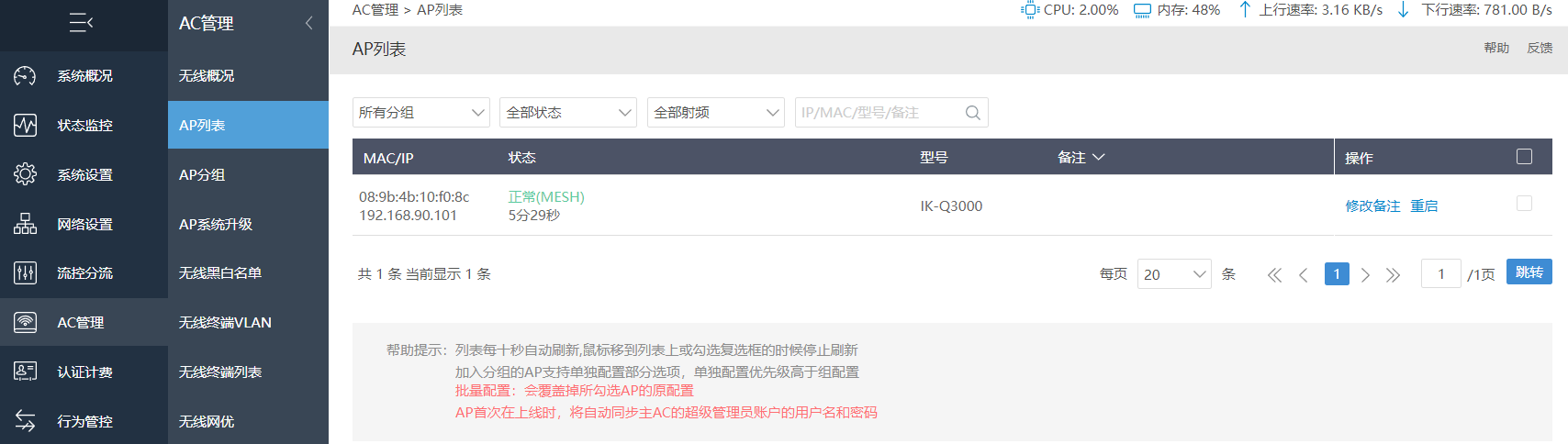
设备连接无线后，上网信息会显示到无线终端列表。在列表中可查看设备连接的AP信息，确认所连接的Mesh设备。

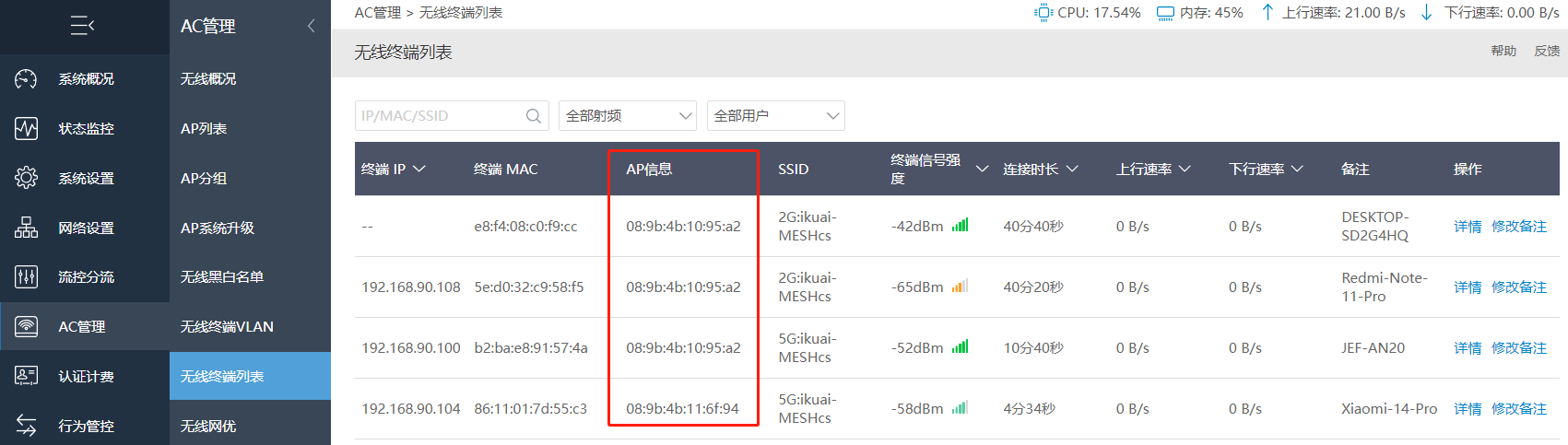
Mesh快连中也能查看对应从设备下在线终端。

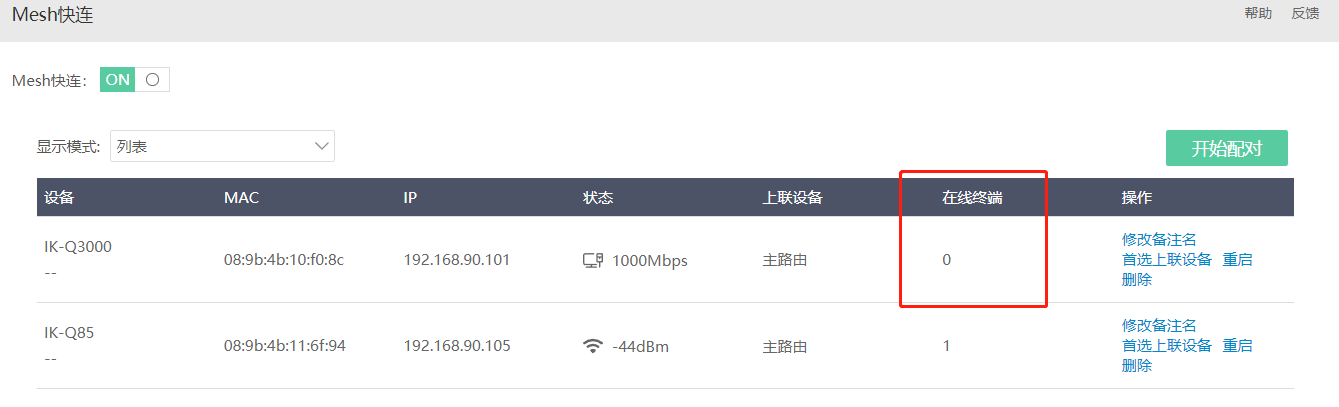
无线Mesh：

网络拓扑：

设备版本：3.7.12企业版。

配置要求：从设备需恢复默认配置。

拓扑说明：设备接入电源，主设备连接外网线路。WEB页面操作在主设备均可完成，从设备无需进入WEB页面。

注意：mesh从设备默认绑定主设备的LAN1接口，且不支持配置，LAN1接口如果没有开启DHCP服务，mesh网络将无法自动获取IP地址

实现目的：通过Mesh功能实现无线信号的延续。

在网络设置--Mesh快连，开启Mesh快连。

按照页面提示检查设备亮灯情况以及设备摆放位置。一切准备就绪后，点击开始配对。

页面出现配对画面。

Mesh对接亮灯情况：

Q6000：

对接时：红绿灯交替闪烁。

对接成功：绿灯长亮。

Q3000：

对接时：彩灯交替闪烁，如对接时无灯闪烁，可按Mesh键3次。

对接成功：粉色灯长亮。

对接成功后设备灯显示效果：

配对时页面会显示网络中所有从设备MAC地址，MAC地址全面扫描完成后，点击停止配对。

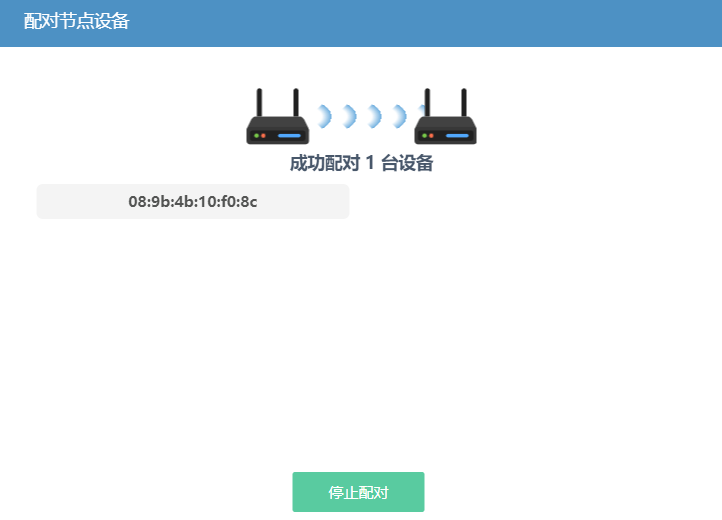
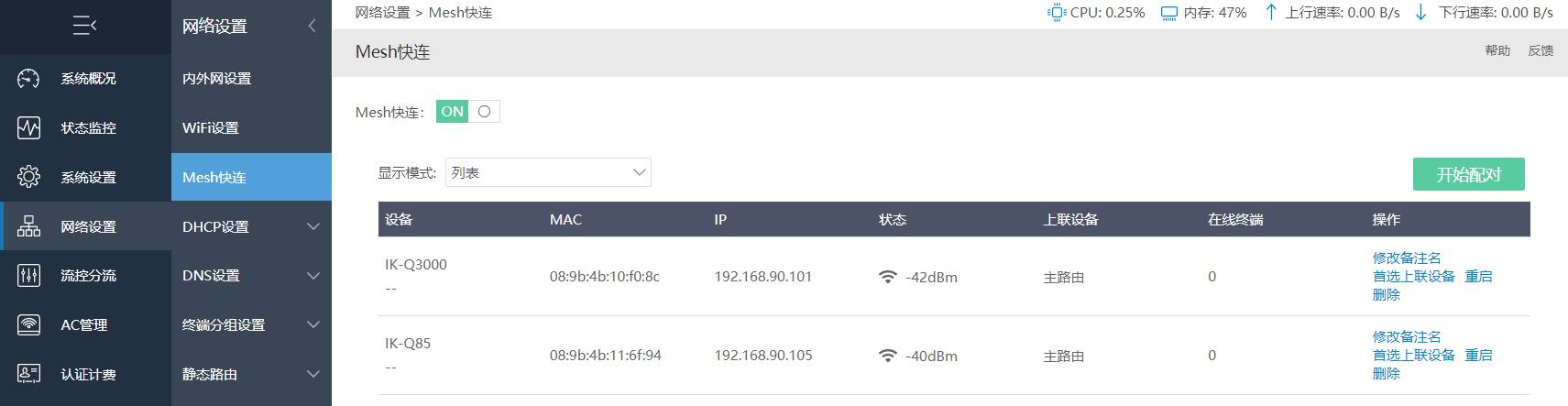
配对成功后，在列表模式下，会显示配对的设备名称、MAC地址、设备信号状态、上联设备。如网络中有多个上联设备情况下，可点击操作处“首选上联设备”选择对应上联设备MAC信息。

在显示模式中切换模式为”拓扑”会显示当前Mesh组网拓扑图。

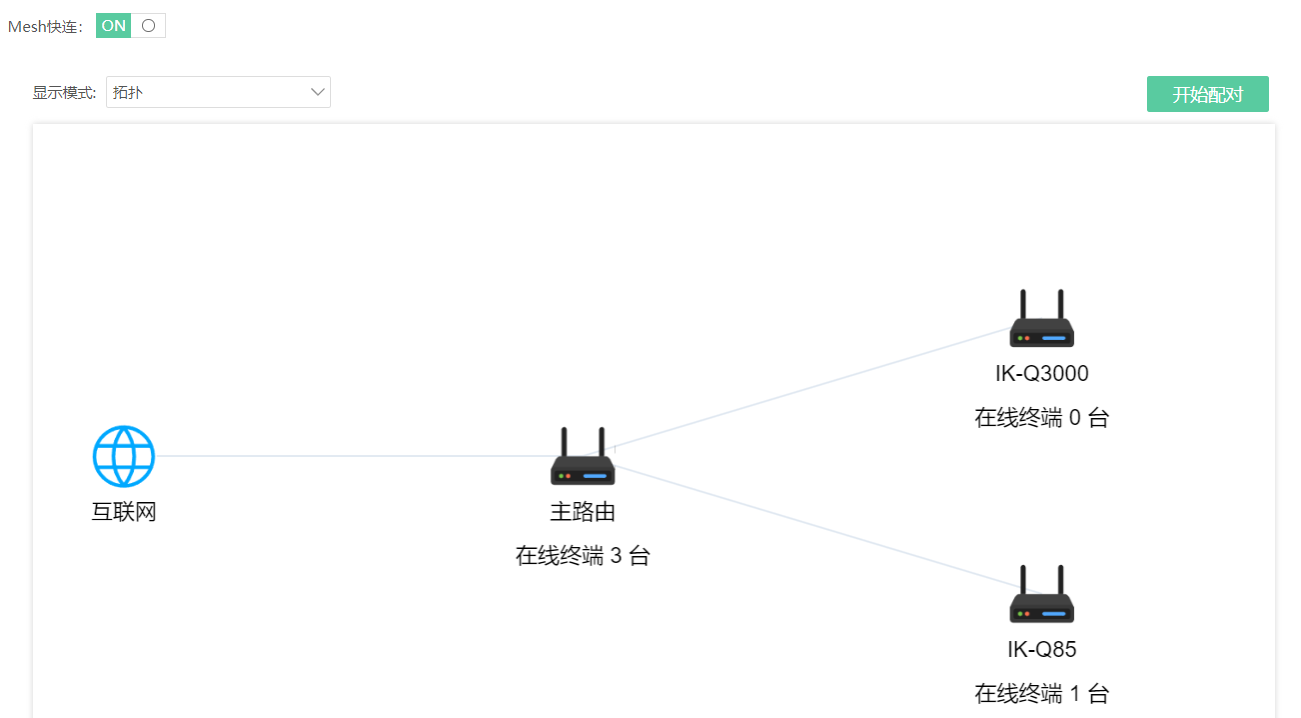
Mesh对接成功后设置无线名称，进行Mesh快连测试。

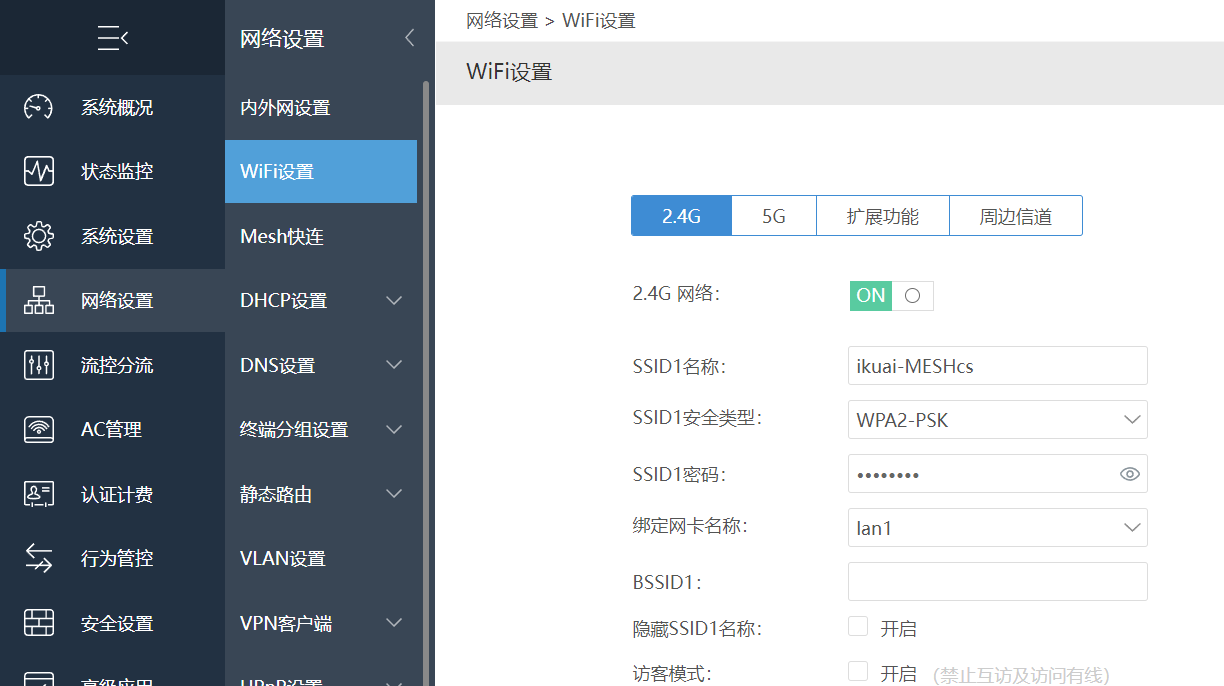
在AC管理--AP列表会显示Mesh设备。

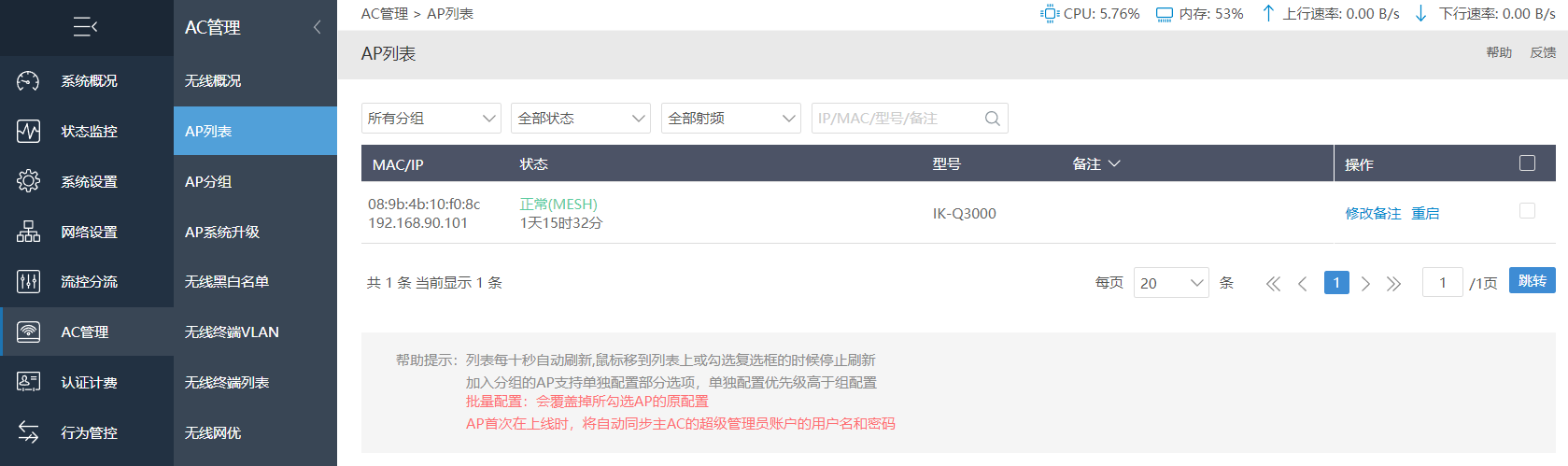
设备连接无线后，上网信息会显示到无线终端列表。在列表中可查看设备连接的AP信息，确认所连接的Mesh设备。

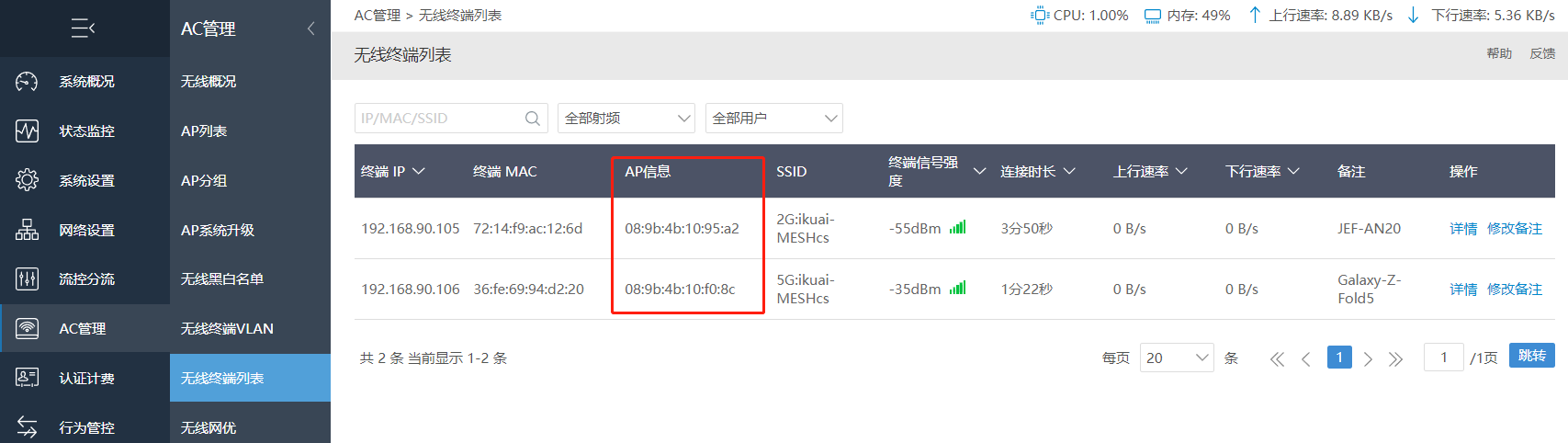
Mesh快连中也能查看对应从设备下在线终端。

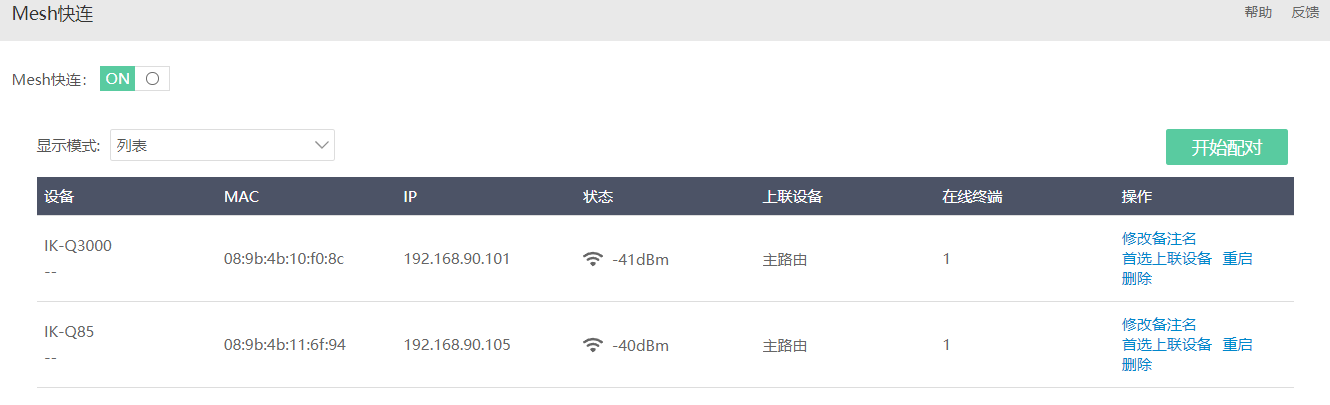
注意事项：

1. Mesh快连目前仅支持组建4级（包含主路由）。

Mesh有效拓扑类型：

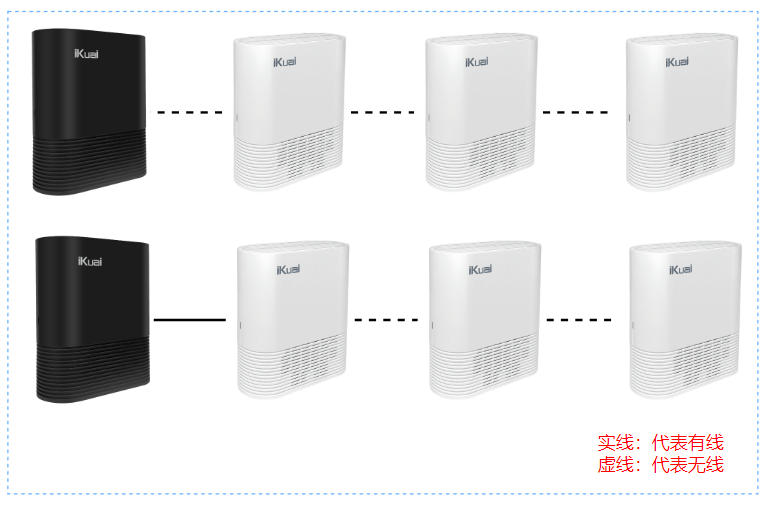
Mesh无效拓扑类型：

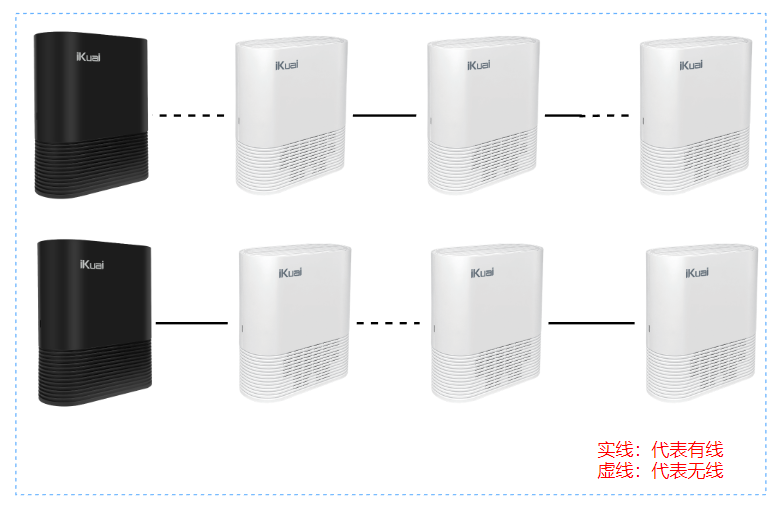
简单的解释: 二级以下的节点,如果接一根线到另外一台的wan口, 这样可能会出异常(两台设备会互相连,导致死循环)

解决的方法: 在Mesh快连的页面，将该二级节点设置首选上联设备为 主路由即可