哈希表(HashMap)与字符串哈希

哈希表

哈希表是一种通过映射来快速查找的数据结构。其通过键值对(key-value)来存储。一个数据通过哈希函数的运算来生成一个属于他自己的键值，尔后将其与键值绑定。当我们想查找这个数据时，就可以直接通过键来访问对应的值，时间复杂度近似为O(1)。

哈希表适用于这样一种场景，当数据范围很大但是数据量很小时(不要求保序，若保序可以考虑离散化)，或者对于一个字符串我们想要使用数字值对其做出映射时(字符串哈希)，都可以使用哈希表来存储，当查找对应值时，只需要计算出键来找就好了。而不需要从头到尾遍历。

数字哈希

对于数据规模为N一个数字，我们可以给出这样一个简单的哈希函数

int get_key(int x)
{
	return x % N;
	//若考虑x可能为一负数
	return (x % N + N) % N;
}

显然对于数据范围内的数据，计算出的哈希值肯定会有所冲突，这就导致一个哈希值无法对应多个数据的存储。这里给出解决冲突的两个方案，分离链接法(拉链法)以及开放定址法

分离链接法(拉链法)：



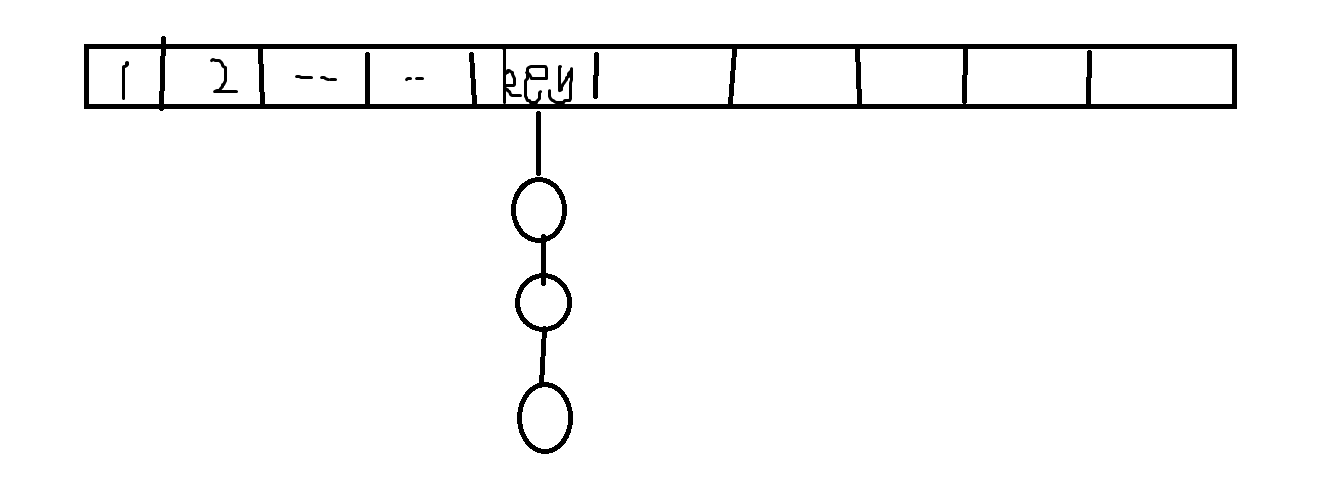
示意图如上

顾名思义，拉链法就是在对应每个哈希值下建立一条链表，当该哈希值有元素要加入时，就在对应哈希值的链表上插入一个新节点。(有点像邻接表)在查找时，我们根据对应的哈希值来遍历整条链表来寻找对应元素。链表的实现可以使用数组模拟，也可以这样

vector<int>h[N]；

这样每一个数组元素都是一个节点，链表插入元素也就变为了h[i].push_back(x);

开放定址法：

开放定址法的实现很简单。在初始化存储数组时，将其中的元素都置为一不可触碰到初始值(如负数或者无穷大0x3f3f3f3f)。当遇到冲突时，我们就接着看下一个存储位置是否没有元素存储，直到找到一个没有元素存储的位置，存储进去。查找时也是，若当前位置已经有元素了，且该元素不为空，就接这查找下一个元素，直到找到x == hi,或者h[i]为空(该表中没有该元素)时截止。

下面给出分离链接法以及开放定址法实现的代码

分离链接法

void insert(int x)
{
	int k = get_hash(x);
	h[k].push_back(x);//加入到链表中
}
bool query(int x)
{
	int k = get_hash(x);
	for (int i = 0; i < h[k].size(); i++)//遍历整条链表
	{
		if (h[k][i] == x)
			return true;
	}
	return false;
}

开放定址法

void insert(int x) // 开放定址法
{
	int k = get_hash(x);
	while (h[k] != null) k++; //若当前位置不为空，向后移一位直到找到空位置
	h[k] = x;
}
bool query(int x)
{
	int k = get_hash(x);
	while (h[k] != null && h[k] != x) k++; //若当前位置不空且并非所查节点，向后移一位
	if (h[k] == x)
		return true; //若能找到这样的节点，则hashmap中有该元素
	else
		return false;//否则代表hashmap中没有该元素
}

最后还有一点需要提醒的是，据经验所得，哈希表的大小N一般取为素数。对于分离链接法取大于数据规模的第一个素数，而对于开放定址法一般取大于数据规模2-3倍的第一个素数，这样的话会使得冲突的概率比较小

字符串哈希

对于数字可以将其映射，那么，对于存储起来比较麻烦的字符串，我们也可以构造一个合适的哈希函数，将一个字符串映射到一个哈希值上，从而达到以较快的速度来处理字符串的查找与对比。

对于字符串的哈希，我们给出这样的思想，将一个长度为p的字符串看作一个p进制数，其哈希函数就是将字符串从p进制转换为十进制。

比如二进制数1010，其基数为2，转换成对应的十进制数时，最低位的权值为0，权值依此逐渐上升。则1010对应的十进制数为$$ 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 10$$。对应的一个p进制数的基数就是p。

举个例子。给出字符串abc，假设其为131进制数，则其对应的十进制数为$$ 'a' * 131^2 + 'b' * 131^1 + 'c' * 131^0 $$,字符取其对应的ascii码来计算，最后防止数据太大，将结果模上一个较大的数如2^64

需要用到字符串哈希的题目，常常是需要给出一个较长的字符串，然后给出n次询问，每次查询该字符串的两个区间内的字串是否相等，这就要求我们能快速求出一个字符串中任意区间内字符的长度，显然，应用前缀和算法可以实现这一点

注意，根据经验，当进制p = 131，mod = 2^64时，字符串哈希可以视为没有冲突。由于字符串哈希计算时仅涉及正数，因此数据可以使用unsigned long long 类型(8个Byte，64个bit，最多存储2^64 - 1个数)来存储，当数据超过2^64 -1溢出时，其效果等于mod 2^64

下面给出预处理字符串哈希前缀和的代码

const int N = 1e5+10,P = 131;
typedef unsigned long long ull;
ull h[N],p[N];

void pre_process(char s[])
{
	p[0] = 1;
	h[0] = 0;
	for (int i = 1; s[i]; i++)
	{
		p[i] = p[i - 1] * P;//p[i]存储的是p^i次幂，后面有用
		h[i] = h[i - 1] * P + s[i];
	}
}

预处理之后如何求出对应区间内的哈希值呢？

给出左右端点[l,r], 其右端点的前缀和哈希为

\[s[0] * p^{r-1} + s[1] * p^{r-2} + ... + s[l - 1] * p^{r - l + 1} + s[l] * p^{r - l} + ... + s[r] * p^0
\]

而其左端点减1的前缀和哈希为（即l - 1）

\[s[0] * p^{l-2} + s[1] * p^{l - 3} + ... + s[l - 1] * p^0
\]

显然，我们让2式乘以 r - l + 1，让其左端与1式对齐得到如下式子

\[s[0] * p^{r-1} + s[1] * p^{r - 2} + ... + s[l - 1] * p^{r - l + 1}
\]

1式减2式，得如下

\[s[l] * p^{r - 1} + s[l - 1] * p^{r - 2} + ... + s[r] * p^0
\]

可以看出，最后得出的三式就是从l到r的前缀哈希和因此我们得出了这样一个公式。要计算从l到r的前缀哈希和，按照下面公式即可

\[ans = h[r] - h[l-1] * p[r - l + 1]
\]

所以得出以下函数

ull get_hash(int l, int r)
{
	return h[r] - h[l - 1] * p[r - l + 1];
}

当我们想要比对两个字符串是否相等时，只需要比对两个字符串的哈希值是否相等即可。给出例题

字符串哈希

STL中的哈希表

在STL库中，unordered_map类是一个已经实现好的哈希表，其初始化如下

#include <unordered_map>
using namespace std;
int main()
{
	unordered_map<string,int> a;//哈希表的键类型和值类型可以任意
	//向哈希表中插入一个元素有如下几种方法
	a.insert({"try1",1});//insert参数为一个pair
	a.emplace("try2",2);//emplace第一个参数为键，第二个参数为值
	a["try3"] = 3;//unordered_map重载了数组运算符，使之可以直接用来添加元素(类似于py中的字典)
	//当我们想要访问其中的元素时，只需要想使用数组一样，不过索引为对应键值
	cout << a["try1"] << endl;
	cout << a["try2"] << endl;
	cout << a["try3"] << endl;
	return 0;
}
//unordered_map的时间复杂度近似O(1)