HDU 2056:Rectangles(两个矩形交点的性质)

一、原题链接

Problem - 2056 (hdu.edu.cn)

二、题面

Given two rectangles and the coordinates of two points on the diagonals of each rectangle,you have to calculate the area of the intersected part of two rectangles. its sides are parallel to OX and OY .

三、示例

1. 输入

   • Input The first line of input is 8 positive numbers which indicate the coordinates of four points that must be on each diagonal.The 8 numbers are x1,y1,x2,y2,x3,y3,x4,y4.That means the two points on the first rectangle are(x1,y1),(x2,y2);the other two points on the second rectangle are (x3,y3),(x4,y4).
     

   • 1.00 1.00 3.00 3.00 2.00 2.00 4.00 4.00
     5.00 5.00 13.00 13.00 4.00 4.00 12.50 12.50
     

2. 输出

   • Output For each case output the area of their intersected part in a single line.accurate up to 2 decimal places.
     

   • 1.00
     56.25
     

五、思路

1. 已知，当给出一个矩形两个对角点的坐标\((x_1,y_1),(x_2,y_2)\)可确定一个矩形的坐标和大小，且该矩形的两边必然与矩形的两边平行

   

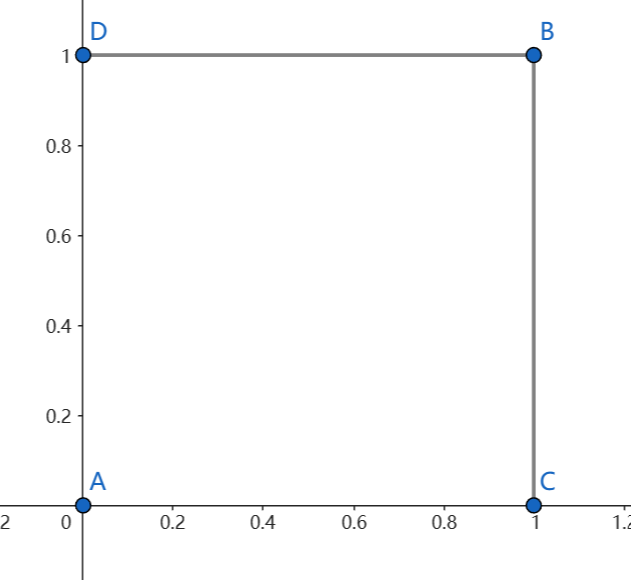
   注：已知对角点A(0,0)，B(1,1)即可知道矩形的坐标与大小

2. 题目中给出了两个矩形的两个对角点坐标，要求相交部分的大小。显然，如果有相交部分，则该相交部分必为与坐标轴平行的矩形，故题目可转化为求该矩形的两个对角点。

   

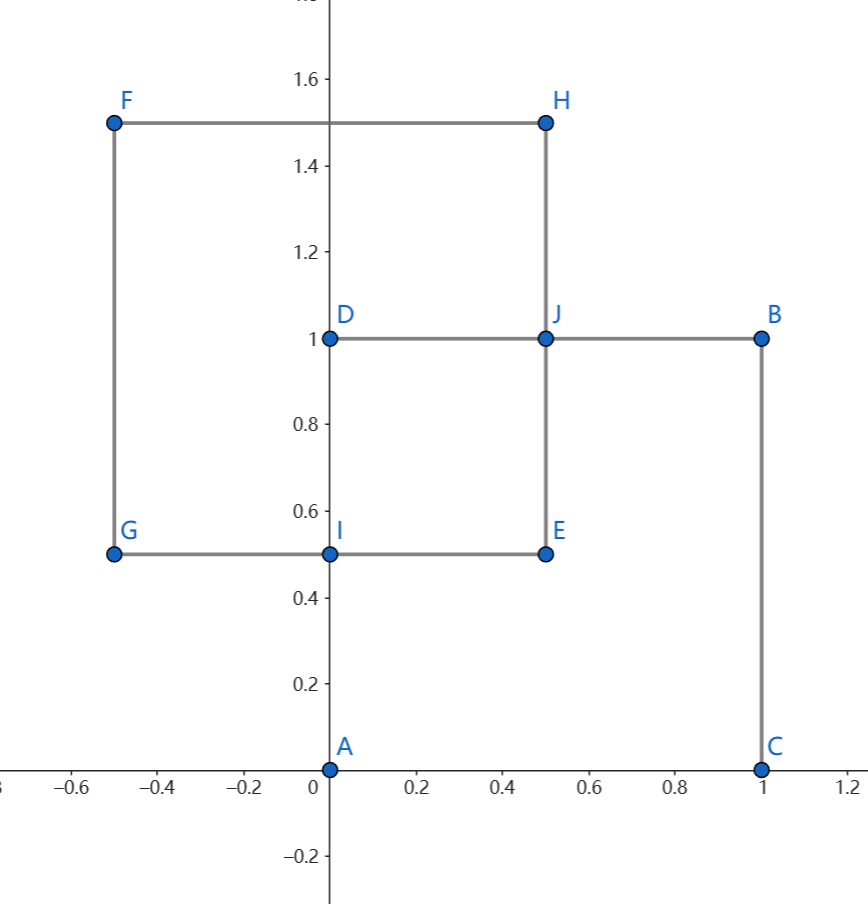
   注：要求相交部分，只需求点I,J即可

3. 如已知两个矩形的对角点坐标\((x_G,y_G),(x_H,y_H),(x_A,y_A),(x_B,y_B)\)，考虑对角点\((x_I,y_I),(x_J,y_J)\)的性质(以x坐标为例)

   • 性质一：在数值上，由于求的是交集，\(x_I,x_J\)必为\(x_G,x_H,x_A,x_B\)的中间数
   • 性质二：由于\(I(x_I,y_I),G(x_G,y_G)\)两点同时在两个矩形上，故有\(x_G<=x_I<=x_H,x_A<=x_I<=x_B\)(\(x_G\)类似)

六、code

#include <bits/stdc++.h>

#define PI 3.1415927

using namespace std;
typedef double elemType;

typedef struct{
    double x,y;
}Point;

bool contain(double num,double range1,double range2){
    if(range1>range2){
        swap(range1,range2);
    }
    return num>=range1&&num<=range2?true:false;
}

int main()
{
    Point p[2][2];  //二维数组：第一维表示第几个矩形，第二位表示第几个点
    double x[4],y[4];
    while(cin >> p[0][0].x >> p[0][0].y >> p[0][1].x >> p[0][1].y >> p[1][0].x >> p[1][0].y >> p[1][1].x >> p[1][1].y){
        //根据性质一：选取可能的交点：交点必然在内部
        int num=0;
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                x[num]=p[i][j].x;
                y[num]=p[i][j].y;
                num++;
            }
        }
        sort(x,x+4);
        sort(y,y+4);
        Point ans[2];
        ans[0].x=x[1];
        ans[1].x=x[2];
        ans[0].y=y[1];
        ans[1].y=y[2];
        //根据性质二：判断两点是否有效
        bool flag=1;
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                if(!contain(ans[i].x,p[j][0].x,p[j][1].x)||!contain(ans[i].y,p[j][0].y,p[j][1].y)){
                    flag=0;
                }
            }
        }
        printf("%.2lf\n",flag?(ans[1].y-ans[0].y)*(ans[1].x-ans[0].x):0);
    }
    return 0;
}