代码随想录Day15

110.平衡二叉树 （优先掌握递归）

给定一个二叉树，判断它是否是 平衡二叉树

平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1。

示例 1：

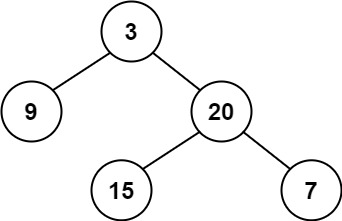
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

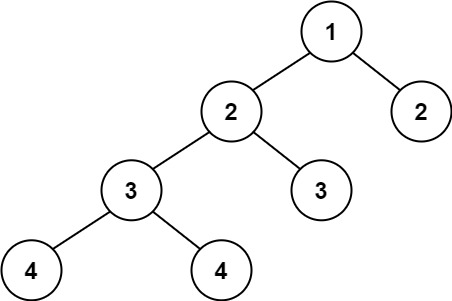
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内

-10⁴ <= Node.val <= 10⁴

---

正解

既然要求比较高度，必然是要后序遍历。

1. 明确递归函数的参数和返回值
   
   参数：当前传入节点。 返回值：以当前传入节点为根节点的树的高度。
   
   那么如何标记左右子树是否差值大于1呢？
   
   如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。
   
   所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。
2. 明确终止条件
   
   递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
3. 明确单层递归的逻辑
   
   如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。
   
   分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。

上代码(●'◡'●)

class Solution {
public:
    // 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1
    int getHeight(TreeNode* node) {
        if (node == NULL) {
            return 0;
        }
        int leftHeight = getHeight(node->left);
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(node->right);
        if (rightHeight == -1) return -1;
        return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;
    }
};

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

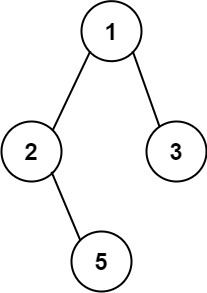
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内

-100 <= Node.val <= 100

---

正解

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

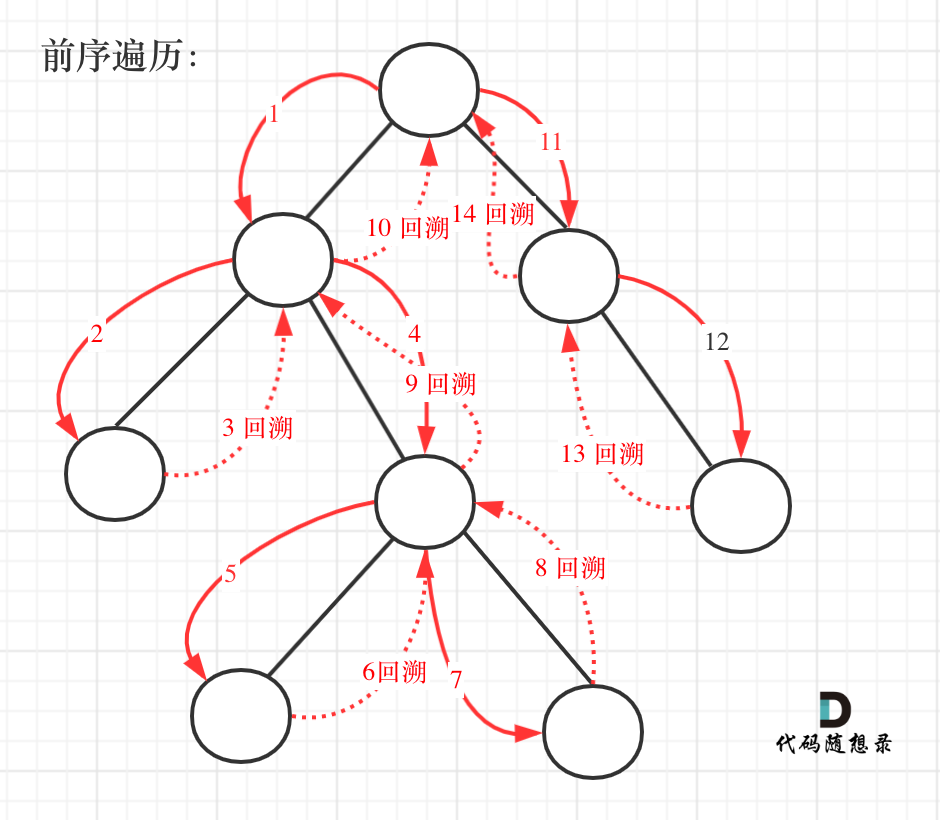
1. 递归函数参数以及返回值
   
   要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值。
2. 确定递归终止条件
   
   当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。
   
   这里使用vector 结构path来记录路径，所以要把vector 结构的path转为string格式，再把这个string 放进 result里。
   
   那么为什么使用了vector 结构来记录路径呢？ 因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。
3. 确定单层递归逻辑
   
   因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。
   
   然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。
   
   所以递归前要加上判断语句，下面要递归的节点是否为空
   
   此时还没完，递归完，要做回溯啊，因为path 不能一直加入节点，它还要删节点，然后才能加入新的节点。
   
   那么回溯要怎么回溯呢？
   
   我们知道，回溯和递归是一一对应的，有一个递归，就要有一个回溯。
   
   所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！

上代码(●'◡'●)

class Solution {
private:

    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) traversal(cur->left, path + "->", result); // 左
        if (cur->right) traversal(cur->right, path + "->", result); // 右
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;

    }
};

404.左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

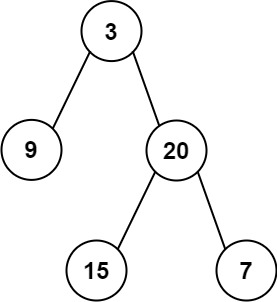
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内

-1000 <= Node.val <= 1000

---

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。

左叶子的明确定义：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点;

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

1. 确定递归函数的参数和返回值
   
   判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int
   
   使用题目中给出的函数就可以了。
2. 确定终止条件
   
   如果遍历到空节点，那么左叶子值一定是0;
   
   注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0;
3. 确定单层递归的逻辑
   
   当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

上代码(●'◡'●)

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if (root == NULL) return 0;
        int leftValue = 0;
        if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
            leftValue = root->left->val;
        }
        return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
    }
};

写博不易，请大佬点赞支持一下8~