最详细STL（二）deque

deque其实也是数组，也可以动态的添加和减少元素，但是和vector不同的是，deque可以快速的在头部和尾部添加减少元素（vector只能快速的在尾部添加），然而在插入元素的时候因为头部和尾部都可以添加元素，deque则会选择最近的一端来迭代过去，并插入元素。不过deque更优势的是，内存空间是不连续的。

一、deque的内存空间是分块的

为了验证不连续，我写了一段代码供大家观赏

#include<cstdio>
#include<deque>
#include<vector>
using namespace std;

int main()
{
    int testnum = 100;
    deque<int> md(testnum+1);// +1防止索引越界
    int issame = 0;
    for(int i=0;i<testnum;i++)
    {
        // 判断是否是连续数组，不是就打印，是就issame++
        if(&md[i+1]-&md[i]!=1)
        {
            printf("%d %d %d %d\n",&md[i+1]-&md[i],&md[i+1],&md[i], issame);
            issame=0;
        }
        else
            issame++;
    }

    return 0;
}

当testnum为100的时候没有输出，说明还是连续的，但是testnum变成1000的时候有了输出，这也就验证了deque是不连续的，当testnum是10000不连续的块就更多了

testnum=100

testnum=1000

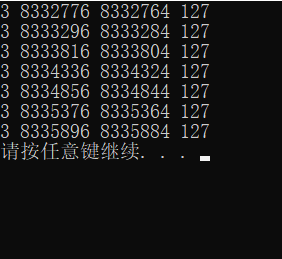
testnum=10000

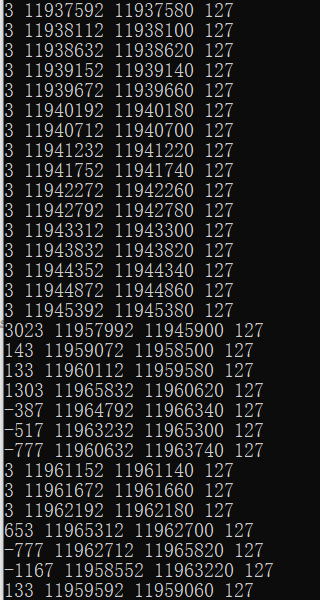
发现规律了没有，每一个连续的块大小都是127然而这样不连续的数据结构可以更好的利用空间，也就是数组和链表的结合版。

下面开始正文了，我来告诉大家deque什么时候用？怎么用？用的时候要注意些什么吧？

二、什么时候用

从上面的小实验得出，deque还是优于vector的，只是空间不连续。忽略空间的连续性和next指针，vector相当于普通链表，而deque就相当于有两个指针分别指向头和尾的链表。所以基本上在没有空间连续的需求，完全deque可以替代vector。

三、怎么用

1.访问元素

方法	解释
d[i]	通过下标访问i位置元素的值
d.at[i]	通过下标访问i位置元素的值
d.front()	访问deque头部元素的值
d.back()	访问deque尾部元素的值
d.begin()	生成头部迭代器（某种意义上的指针）
d.end()	生成尾部迭代器（某种意义上的指针）

2.添加元素

d.push_back(num)	在d的尾部添加num值
d.push_front()	在d的头部添加num值
d.insert(pos,elem)	pos是vector的插入元素的位置
d.insert(pos, n, elem)	在位置pos上插入n个元素elem
d.insert(pos, begin, end)

3.删除元素

d.pop_back()	删除队列尾部元素
d.pop_front()	删除队列头部元素
d.erase(pos)	删除pos位置上的元素
d.erase(begin, end)	删除begin到end区间上的元素，返回下一个元素的位置

4.deque其它操作

d.size()	查看deque的大小
d.empty()	判断deque是否为空
d.clear()	清空deque

四、用的时候要注意什么？

也是和vector一样，需要频繁的在队列中进行元素的增删，这种数据结构还是不适合的

且下标的访问也不要越界