Codeforces 889C Maximum Element（DP + 计数）

题目链接  Maximum Element

题意  现在有这一段求序列中最大值的程度片段：

（假定序列是一个1-n的排列）

int fast_max(int n, int a[]) {
    int ans = 0;
    int offset = 0;
    for (int i = 0; i < n; ++i)
        if (ans < a[i]) {
            ans = a[i];
            offset = 0;
        } else {
            offset = offset + 1;
            if (offset == k)
                return ans;
        }
    return ans;
}

显然这段程序是错误的……有很多可以X掉这段程序的排列

求这样的排列有多少个。

题目是让我们求符合这样条件的排列个数：

1、存在某个数，他比前面的数都大并且小于$n$；

2、他比他后面$k$个数都要大。

假设“中间这个数”为$cnt$

假设$D(i)$为满足$p(i) = i$的这样的排列个数

我们可以把$D(i)$的求解分成两个过程。

1、计算$cnt$等于$i - 1$的排列个数

2、计算$cnt$不等于$i - 1$的排列个数

首先如果$i <= k + 1$，则$D(i) = 0$

当这个序列的$cnt$为$i - 1$时，只要满足$i - 1$和$i$之间的数大于等于$k$个即可。

于是对于$i - 1$这个数的位置的选择，我们有$i - k - 1$种。

然后呢，除了$i - 1$和$i$这两个数，其他数的位置随意（因为$i$排在最后，所以排在$i - 1$前的数字都比$i - 1$要小）

所以当前这种情况对答案的贡献为$(i - k - 1) * (i - 2)!$

考虑另外一种情况。

当$cnt$不等于$i - 1$的时候，一定有$cnt < i - 1$

设$i - 1$所在位置为$pos$，我们把$i - 1$之前的$pos - 1$个数离散化成一个$1$到$pos - 1$的排列

然后在这个排列的最后加上$pos$，就构成了一个$1$到$pos$并且以$pos$结尾的排列

那么如果这个排列是符合要求的，那么整个排列也是符合要求的。

于是我们枚举$i - 1$的位置$pos$，满足条件的位置为$i - k <= pos <= i - 1$

我们在剩下的$i - 2$个数中选出$pos - 1$个放到前$pos - 1$个位置，然后乘上$D(pos)$。

然后还要乘上$(i - pos - 1)!$，因为$i - 1$到$i$之间的数都是随意乱放的……

于是当前这种情况对答案的贡献为

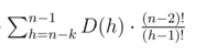
于是我们终于推出了D(n)的公式

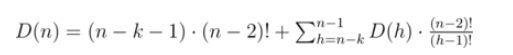
最后的答案怎么计算呢

我们假设$n$的位置为$pos$

那么当$p(pos) = n$的时候，前pos个数的方案数为$D(pos) * C(n - 1, pos - 1)$

后$n - pos$个数的方案数为$(n - pos)!$

所以当$p(pos) = n$的时候对答案的贡献为$D(pos) * C(n - 1, pos - 1)*(n - pos)!$

枚举$pos$，累加即可。

#include <bits/stdc++.h>

using namespace std;

#define rep(i, a, b)	for (int i(a); i <= (b); ++i)
#define dec(i, a, b)	for (int i(a); i >= (b); --i)

const int N  = 1e6 + 10;
const int mod = 1e9 + 7; 

int n, k;
int f[N], s[N];
int fac[N], inv[N];
int ans = 0;

inline int Pow(int a, int b, int mod){
        int ret(1);
        for (; b; b >>= 1, a = (1ll * a * a) % mod) if (b & 1) (ret = 1ll * ret * a) % mod;
        return ret;
}	

void init(){
	fac[0] = 1;
	rep(i, 1, 1e6 + 1) fac[i] = 1ll * fac[i - 1] * i % mod;
	rep(i, 1, 1e6 + 1) inv[i] = Pow(fac[i], mod - 2, mod);
}

inline void up(int &a, int b)   { a = (0ll + a + b) % mod;}
inline void mulup(int &a, int b){ a = 1ll * a * b % mod;}

int main(){

	scanf("%d%d", &n, &k);
	init();

	rep(i, k + 2, n){
		f[i] = i - k - 1;
		up(f[i], s[i - 1] - s[i - k - 1]);
		mulup(f[i], fac[i - 2]);
		s[i] = (0ll + s[i - 1] + 1ll * f[i] * inv[i - 1] % mod) % mod;
	}

	rep(i, 1, n) up(ans, (int)1ll * f[i] * fac[n - 1] % mod * inv[i - 1] % mod);
	printf("%d\n", ans);
	return 0;
}