FFT题集
FFT学习参考这两篇博客，很详细，结合这看，互补。
很大一部分题目需要构造多项式相乘来进行计数问题。
1. HDU 1402 A * B Problem Plus
把A和B分别当作多项式的系数。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std; const double PI = acos(-1.0);
const int maxn = 5e4+;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[];
void FFT(Complex* a,int len,int DFT) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(DFT**PI/m),sin(DFT**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(DFT == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
char coA[maxn],coB[maxn];
///把每一位作为系数 ///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<16)<2*n-2<(1<<17)
Complex a[135000],b[135000];
int ans[]; int main()
{
while(scanf("%s",coA)!=EOF)
{
int lenA = strlen(coA);
int mia = ;
while((<<mia)<lenA) mia++; ///2^mia>=lenA
scanf("%s",coB);
int lenB = strlen(coB);
int mib = ;
while((<<mib)<lenB) mib++;
int len(<<(max(mia,mib)+));
for(int i=;i<len;i++)
{
if(i<lenA) a[i] = Complex(coA[lenA-i-]-'',); ///表示系数,A数组从左往右存了进去 2000 --> 0002
else a[i] = Complex(,);
if(i<lenB) b[i] = Complex(coB[lenB-i-]-'',);
else b[i] = Complex(,);
}
///求A和B的点值表达式
FFT(a, len, );
FFT(b, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * b[i]; ///求C的点值
FFT(a, len, -); ///逆DFT得到系数
for(int i = ; i < len; i++)
ans[i] = (int)(a[i].real + 0.5); ///四舍五入
for(int i = ; i <len - ; i++)
{
ans[i + ] += ans[i] / ;
ans[i] %= ;
}
bool flag = ;
for(int i = len - ; i >= ; i--) ///防止出现前导0
{
if(ans[i]) printf("%d",ans[i]), flag = ;
else if(flag || i == ) printf("");
}
puts("");
}
return ;
}
Code
2.Golf Bot
从K中选两个或者1个，选两个相当于指数相加，比如x^5与x^1相乘，相当于5和1都被选了，直接相加，所以把k中的数字当成系数1，没出现过当成系数0。
对于选1个的可以把x^0的系数设为1.
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
using namespace std; const double PI = acos(-1.0);
const int maxn = 2e5+;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[];
void FFT(Complex* a,int len,int DFT) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(DFT**PI/m),sin(DFT**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(DFT == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
int coA[maxn];
///把每一位作为系数
///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<16)<2*n-2<(1<<17)
Complex a[540000];
int ans[];
int num[maxn];
int main()
{
// freopen("1.txt","r",stdin);
int n,m;
while(scanf("%d", &n)!=EOF)
{
memset(coA, , sizeof(coA));
int maxv = ;
for(int i = ; i < n; i++)
{
int x;
scanf("%d", &x);
coA[x] = ;
maxv = max(maxv, x);
}
coA[] = ;
int mia = ;
while(( << mia) < maxv) mia++;
int len = ( << (mia + ));
for(int i = ; i < len; i++)
{
if(i <= maxv && coA[i]) a[i] = Complex(,);
else a[i] = Complex(, );
}
///求A和B的点值表达式
FFT(a, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * a[i]; ///求C的点值
FFT(a, len, -); ///逆DFT得到系数
memset(ans,,sizeof(ans));
for(int i = ; i < len; i++)
ans[i] = (int)(a[i].real + 0.5); ///四舍五入
int cnt = ;
scanf("%d", &m);
for(int i = ; i < m; i++)
{
int x;
scanf("%d", &x);
if(ans[x]) cnt++;
}
printf("%d\n",cnt);
}
return ;
}
Code
3.HDU - 4609 3-idiots
之前做过给定n个数，任意两个数求和，求总共有多少个不同的，每个数出现过它的系数标记为1，这样FFT后，某个系数不等于0就代表这个数出现过。
这个题，算两个边求和，然后枚举另一条边，算能构成三角形的次数。
以下以1 3 3 4为例。
把长度归为指数后，次数归为系数后，指数从大到小变成{1，2，0，1，0}，自己卷积自己{1，2，0，1，0} * {1，2，0，1，0}
得到{1，4，4，2，4，0，1，0，0}，代表每一个和出现的次数，用ans数组表示
因为构成三角形，不能两次取同一根棍，所以减去两次用同一根棍的
for(int i = 0; i < n; i++) ans[a[i] + a[i]]--;
还有因为卷积的时候，1 4 和 4 1有了顺序，我们在选三角形的时候是没有顺序的，所以要/2
for(int i = 0; i <= len; i++) ans[i] /= 2;
为了后面统计方便，我们求个ans的前缀和，得到sum数组。
我们对所有边排个序，然后枚举一条边a[i],我们假设它是所选三角形里面长度最大的，那么我们能够成三角形的条件之一是两边之和 > a[i]，所以 cnt[i] += sum[len] - sum[a[i]].
但是这里面的和有不符合条件的：
1.一大一小，cnt -= (n - i - 1) * i;
2.一个是它本身，另一个是其他，cnt -= (n-1);
3.两个都是大于的，C(n - i - 1, 2)
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
using namespace std;
typedef long long ll;
const double PI = acos(-1.0);
const int maxn = ( << ) + ;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[maxn];
void FFT(Complex* a,int len,int DFT) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(DFT**PI/m),sin(DFT**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(DFT == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
int coA[maxn];
///把每一位作为系数
///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<17)<2*n-2<(1<<18)
Complex a[maxn];
ll sum[maxn];
ll ans[maxn];
int bran[maxn];
int main()
{
// freopen("1.txt","r",stdin);
int T; scanf("%d", &T);
int n;
while(T--)
{
scanf("%d", &n);
memset(coA, , sizeof(coA));
int maxv = ;
for(int i = ; i < n; i++)
{
int x;
scanf("%d", &x);
bran[i] = x;
coA[x]++;
}
sort(bran, bran + n);
int mia = ;
while(( << mia) < (bran[n - ] + ) ) mia++;
int len = ( << (mia + ));
for(int i = ; i < len; i++)
{
if(coA[i]) a[i] = Complex(coA[i], );
else a[i] = Complex(, );
}
///求A和B的点值表达式
FFT(a, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * a[i]; ///求C的点值
FFT(a, len, -); ///逆DFT得到系数
memset(sum, , sizeof(sum));
for(int i = ; i < len; i++)
ans[i] = (ll)(a[i].real + 0.5); ///四舍五入
for(int i = ; i < n; i++) ans[bran[i] + bran[i]]--;
for(int i = ; i < len; i++)
{
ans[i] /= 2LL;
sum[i] = sum[i - ] + ans[i];
}
ll cnt = ;
for(int i = ; i < n; i++)
{
cnt += sum[len - ] - sum[bran[i]];
cnt -= (ll)(n - i - ) * i;
cnt -= (ll)(n - );
cnt -= (ll)(n - i - ) * (n - i - ) / ;
}
ll all = (ll)n * (n - ) * (n - ) / 6LL;
printf("%.7f\n", (double)cnt / all);
}
return ;
}
Code
4. K-neighbor substrings
字符串的这一类型变换最近已经碰到四道了，以这道题为例，学习这一类算法。
一开始看题解，好多人都说，要把B串翻转，我一直在想为什么翻转
看完这两个文章后，
https://blog.csdn.net/q582116859/article/details/77248970
https://www.zhihu.com/question/22298352
我发现我一直纠结与卷积代码的实现，而忽略了卷积数学公式的书写。
以知乎中掷两颗色子，和为4为例。
看完这个例子就明白了为啥要逆序，因为B串是逆序比较的。
最后得到的卷子公式
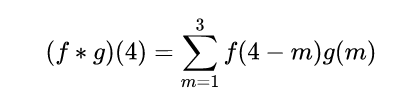
4 - m + m = 4,代表两个因变量之和是4，
到我们这道题，就是
这个上面有点问题，X是从0~n-1,Y是0~m-1.
最后以i开头的字符比较，Hamming距离都累加到 i + m - 1上了。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
#include <set>
using namespace std;
typedef unsigned long long ll;
const double PI = acos(-1.0);
const int maxn = ( << ) + ;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[maxn];
void DFT(Complex* a,int len,int flag) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(flag**PI/m),sin(flag**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(flag == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
///把每一位作为系数
///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<17)<2*n-2<(1<<18)
Complex a[maxn];
Complex b[maxn];
int num[maxn];
void FFT(int len)
{
DFT(a, len, );
DFT(b, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * b[i];
DFT(a, len, -);
for(int i = ; i < len; i++)
num[i] += (int)(a[i].real + 0.5);
}
int coA[maxn];
char s1[maxn];
char s2[maxn];
#define pow Pow
ll pow[maxn];
ll Hash[maxn];
ll magic = ;
///hash利用自然数溢出来取模
set<ll> st;
int main()
{
int K, kase = ;
pow[] = ;
for(int i = ; i < maxn; i++) pow[i] = pow[i - ] * magic;
while(scanf("%d", &K) && K != -)
{
scanf("%s %s", s1, s2);
int la = strlen(s1);
int lb = strlen(s2);
printf("Case %d: ", ++kase);
if(la < lb)
{
puts("");
continue;
}
int mi = ;
while(( << mi) < (max(la, lb) + )) mi++;
int len = ( << (mi + ));
for(int i = ; i < lb / ; i++) swap(s2[i], s2[lb - i - ]);
///A串的a取1，B串的b取1
memset(num, , sizeof(num));
for(int i = ; i < len; i++)
{
if(i < la) a[i] = Complex((s1[i] == 'a' ? : ), );
else a[i] = Complex(, );
if(i < lb) b[i] = Complex((s2[i] == 'b' ? : ), );
else b[i] = Complex(, );
}
FFT(len);
for(int i = ; i < len; i++)
{
// printf("%d ", num[i]);
}
for(int i = ; i < len; i++)
{
if(i < la) a[i] = Complex((s1[i] == 'b' ? : ), );
else a[i] = Complex(, );
if(i < lb) b[i] = Complex((s2[i] == 'a' ? : ), );
else b[i] = Complex(, );
}
FFT(len);
Hash[] = ;
for(int i = ; i < la; i++) Hash[i + ] = Hash[i] * magic + (ll)(s1[i] - 'a' + );
int cnt = ;
st.clear();
for(int i = lb - ; i < la; i++)
{
// printf("%d ",num[i]);
ll now = Hash[i + ] - Hash[i - lb + ] * pow[lb];
if(st.count(now)) continue;
if(num[i] <= K)
{
st.insert(now);
cnt++;
}
}
printf("%d\n", cnt);
}
return ;
} Code
Code
5. Rock Paper Scissors Lizard Spock.
会了上面的字符串的题，这种类型的就差不多会了。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
#include <set>
using namespace std;
typedef unsigned long long ll;
const double PI = acos(-1.0);
const int maxn = ( << ) + ;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[maxn];
void DFT(Complex* a,int len,int flag) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(flag**PI/m),sin(flag**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(flag == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
///把每一位作为系数
///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<17)<2*n-2<(1<<18)
Complex a[maxn];
Complex b[maxn];
int num[maxn];
void FFT(int len)
{
DFT(a, len, );
DFT(b, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * b[i];
DFT(a, len, -);
for(int i = ; i < len; i++)
num[i] += (int)(a[i].real + 0.5);
}
char s1[maxn];
char s2[maxn];
int la, lb, len;
void calc(char win, char lose)
{
for(int i = ; i < len; i++)
{
if(i < la) a[i] = Complex((s1[i] == lose ? : ), );
else a[i] = Complex(, );
if(i < lb) b[i] = Complex((s2[i] == win ? : ), );
else b[i] = Complex(, );
}
FFT(len);
}
int main()
{
scanf("%s %s", s1, s2);
la = strlen(s1);
lb = strlen(s2);
for(int i = ; i < lb / ; i++) swap(s2[i], s2[lb - - i]);
int mi = ;
while(( << mi) < (max(la, lb) + )) mi++;
len = ( << (mi + ));
///A串的a取1，B串的b取1
memset(num, , sizeof(num));
calc('S', 'P');
calc('P', 'R');
calc('R', 'L');
calc('L', 'K');
calc('K', 'S'); calc('S', 'L');
calc('L', 'P');
calc('P', 'K');
calc('K', 'R');
calc('R', 'S');
int ans = ;
for(int i = lb - ; i < la; i++)
{
ans = max(ans, num[i]);
}
printf("%d\n", ans);
return ;
}
Code
6.Educational Codeforces Round 40 Yet Another String Matching Problem
FFT + 并查集。
这个字符串处理的比前面的难了一些。
首先处理如何计算两个相同长度的串。
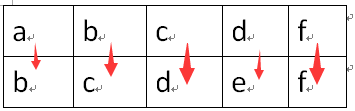
相同位的字母间连边，最后得到这样的图：
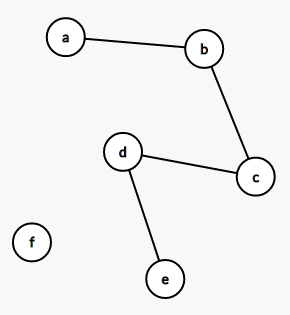
找到了一个好用的画图软件，再也不用画图板了。。。https://csacademy.com/app/graph_editor/
那最后的距离就是不同的节点个数 - 联通块个数 = 6 - 2 = 4，为什么呢
首先，我们先要明白，一个联通块的节点，最后都会变成同一个字母，
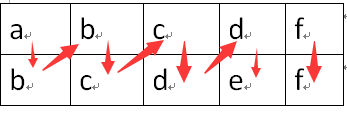
比如全变成e。那一个联通块内不同的节点就是总个数 - 1，所以总的就是 总个数 - 联通块个数。
现在再来考虑题目：
我们把每一次比较当成一个无向图，那么最多有 n - m + 1个无向图。
下面就像正常的FFT那样计算，比如 上面的串中'a'设为1，下面的串'b'设为1，FFT后，
系数为1的点，代表此无向图中，有a --> b这条边，因为只有a~f这6个字母，所以每个无向图的节点只有6个，直接跑并查集就可以了。
时间复杂度O(30nlogn)。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
#include <set>
using namespace std;
typedef unsigned long long ll;
const double PI = acos(-1.0);
const int maxn = ( << ) + ;
struct Complex
{
double real,image; ///实部和虚部
Complex(double _real,double _image)
{
real = _real;
image = _image;
}
Complex(){}
}; Complex operator + (const Complex &c1,const Complex &c2)
{
return Complex(c1.real+c2.real,c1.image+c2.image);
} Complex operator - (const Complex &c1,const Complex &c2)
{
return Complex(c1.real-c2.real,c1.image-c2.image);
} Complex operator * (const Complex &c1,const Complex &c2)
{
return Complex(c1.real*c2.real-c1.image*c2.image, c1.real*c2.image + c1.image * c2.real);
} int rev(int id,int len)
{
int ret = ;
for(int i=;(<<i)<len;i++)
{
ret <<= ;
if(id & (<<i)) ret |= ;
}
return ret;
}
Complex A[maxn];
void DFT(Complex* a,int len,int flag) ///对a进行DFT或者逆DFT,结果存在a当中
{
for(int i = ; i < len; i++)
A[rev(i,len)] = a[i]; ///按其在叶子节点中的顺序存储
for(int s = ; ( << s)<= len; s++)
{
int m = ( << s);
Complex wm = Complex(cos(flag**PI/m),sin(flag**PI/m)); ///主n次单位根
for(int k = ; k < len; k += m)
{
Complex w = Complex(, ); ///旋转因子
for(int j = ; j < (m >> ); j++)
{
Complex t = w * A[k + j + (m >> )];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> )] = u - t;
w = w * wm;
}
}
}
if(flag == -) for(int i = ; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = ; i < len; i++) a[i] = A[i];
return;
}
///把每一位作为系数
///乘积后次数最大为2 * n - 2,转换成2的k次幂，(1<<17)<2*n-2<(1<<18)
Complex a[maxn];
Complex b[maxn];
int num[maxn];
void FFT(int len)
{
DFT(a, len, );
DFT(b, len, );
for(int i = ; i < len; i++)
a[i] = a[i] * b[i];
DFT(a, len, -);
for(int i = ; i < len; i++)
num[i] = (int)(a[i].real + 0.5);
}
char s1[maxn];
char s2[maxn];
int la, lb, len;
int pre[maxn][];
void calc(char l, char r)
{
for(int i = ; i < len; i++)
{
if(i < la) a[i] = Complex((s1[i] == l ? : ), );
else a[i] = Complex(, );
if(i < lb) b[i] = Complex((s2[i] == r ? : ), );
else b[i] = Complex(, );
}
FFT(len);
}
int Find(int i, int x)
{
if(x == pre[i][x]) return x;
return pre[i][x] = Find(i, pre[i][x]);
}
set<int> st[maxn];
int main()
{
scanf("%s %s", s1, s2);
la = strlen(s1);
lb = strlen(s2);
for(int i = ; i < lb / ; i++) swap(s2[i], s2[lb - - i]);
int mi = ;
while(( << mi) < (max(la, lb) + )) mi++;
len = ( << (mi + ));
///A串的a取1，B串的b取1
for(int i = lb - ; i < la; i++)
{
for(int j = ; j < ; j++)
{
pre[i][j] = j;
}
}
memset(num, , sizeof(num));
for(int i = ; i < ; i++)
{
for(int j = ; j < ; j++)
{
if(i == && j == )
{
int ccc = ;
}
int u = i, v = j;
calc(u + 'a', v + 'a');
for(int k = lb - ; k < la; k++)
{
if(num[k]) ///代表有边
{
int x = Find(k, u);
int y = Find(k, v);
pre[k][x] = pre[k][y];
st[k].insert(u);
st[k].insert(v);
}
}
}
}
for(int i = lb - ; i < la; i++)
{
int cnt = ;
for(int j = ; j < ; j++)
{
if(pre[i][j] == j && (st[i].count(j))) cnt++;
}
printf("%d ", st[i].size() - cnt);
}
return ;
}
Code
FFT题集的更多相关文章
- ACM题集以及各种总结大全！
ACM题集以及各种总结大全! 虽然退役了,但是整理一下,供小弟小妹们以后切题方便一些,但由于近来考试太多,顾退役总结延迟一段时间再写!先写一下各种分类和题集,欢迎各位大牛路过指正. 一.ACM入门 关 ...
- 全国各大 oj 分类题集...
各种题集从易到难刷到手软 你准备好了吗? 准备剁手吧
- ACM题集以及各种总结大全（转）
ACM题集以及各种总结大全! 虽然退役了,但是整理一下,供小弟小妹们以后切题方便一些,但由于近来考试太多,顾退役总结延迟一段时间再写!先写一下各种分类和题集,欢迎各位大牛路过指正. 一.ACM入门 关 ...
- 组合数取模&&Lucas定理题集
题集链接: https://cn.vjudge.net/contest/231988 解题之前请先了解组合数取模和Lucas定理 A : FZU-2020 输出组合数C(n, m) mod p (1 ...
- Bug是一种财富-------研发同学的错题集、测试同学的遗漏用例集
此文已由作者王晓明授权网易云社区发布. 欢迎访问网易云社区,了解更多网易技术产品运营经验. 各位看官,可能看到标题的你一定认为这是一篇涉嫌"炒作"的文章,亦或是为了吸引眼球而起的标 ...
- 数位dp题集
题集见大佬博客 不要62 入门题,检验刚才自己有没有看懂 注意一些细节. 的确挺套路的 #include<bits/stdc++.h> #define REP(i, a, b) for(r ...
- 二级C语言题集
时间:2015-5-13 18:01 在131题之后是按考点分类的题集,有需要的朋友可以看一下 ---------------------------------------------------- ...
- 中南大学2019年ACM寒假集训前期训练题集(基础题)
先写一部分,持续到更新完. A: 寒衣调 Description 男从戎,女守家.一夜,狼烟四起,男战死沙场.从此一道黄泉,两地离别.最后,女终于在等待中老去逝去.逝去的最后是换尽一生等到的相逢和团圆 ...
- 【转】并查集&MST题集
转自:http://blog.csdn.net/shahdza/article/details/7779230 [HDU]1213 How Many Tables 基础并查集★1272 小希的迷宫 基 ...
随机推荐
- 【php】【异步】php实现异步的几种方法
请参考 4种php常用的异步执行方式 ajax 和 img 的 src 属性 系统指令调用 (在php代码里面调用系统指令) curl socket通信
- 李涛ps高手之路
下载地址:http://www.ly89.cn/detailR/21.html
- python 程序小测试
python 程序小测试 对之前写的程序做简单的小测试 ... # -*- encoding:utf-8 -*- ''' 对所写程序做简单的测试 @author: bpf ''' def GameOv ...
- matplotlib学习记录 三
# 绘制自己和朋友在各个年龄的女友数量的折线图 from matplotlib import pyplot as plt # 让matplotlib能够显示中文 plt.rcParams['font. ...
- uncaught exception 'NSInternalInconsistencyException, reason:[UITableViewController loadView] loaded the "Controller" nib but didn't get a UITableView
http://blog.csdn.net/ryantang03/article/details/7941058#reply 上面那篇文章是我查找的ios实现下拉刷新功能,在我下载完代码运行的过程中发现 ...
- HDU - 6199 gems gems gems （DP）
有n(2e4)个宝石两个人轮流从左侧取宝石,Alice先手,首轮取1个或2个宝石,如果上一轮取了k个宝石,则这一轮只能取k或k+1个宝石.一旦不能再取宝石就结束.双方都希望自己拿到的宝石数比对方尽可能 ...
- window 7上安装Visual Studio 2017失败的解决方法
今天在办公电脑上windows 7系统上装Visual Studio 2017企业版的时候遇到了一个让人懵逼的错误. 为啥说懵逼呢,因为昨天楼主在台式机上同样安装2017没有任何问题啊,台式机上是wi ...
- HDU 3072 SCC Intelligence System
给出一个带权有向图,要使整个图连通.SCC中的点之间花费为0,所以就先缩点,然后缩点后两点之间的权值为最小边的权值,把这些权值累加起来就是答案. #include <iostream> # ...
- nuc 第二届山西省大学生程序设计大赛 魔力手环
problem 很妙啊--发现状态转移矩阵每一行都可以由上一行平移得到,每次只算第一行然后平移,\(O(n^3)\) 就变成了 \(O(n^2)\). #include <iostream> ...
- 如何在官网下载Spring jar包
该链接里面讲的很仔细! http://blog.csdn.net/frankarmstrong/article/details/69808813