codeforces练习

DZY Loves Colors

Time Limit:2000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-07-07)

Description

DZY loves colors, and he enjoys painting.

On a colorful day, DZY gets a colorful ribbon, which consists of n units (they are numbered from 1 to n from left to right). The color of the i-th unit of the ribbon is i at first. It is colorful enough, but we still consider that the colorfulness of each unit is 0 at first.

DZY loves painting, we know. He takes up a paintbrush with color x and uses it to draw a line on the ribbon. In such a case some contiguous units are painted. Imagine that the color of unit i currently is y. When it is painted by this paintbrush, the color of the unit becomes x, and the colorfulness of the unit increases by |x - y|.

DZY wants to perform m operations, each operation can be one of the following:

1. Paint all the units with numbers between l and r (both inclusive) with color x.
2. Ask the sum of colorfulness of the units between l and r (both inclusive).

Can you help DZY?

Input

The first line contains two space-separated integers n, m (1 ≤ n, m ≤ 10⁵).

Each of the next m lines begins with a integer type (1 ≤ type ≤ 2), which represents the type of this operation.

If type = 1, there will be 3 more integers l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 10⁸) in this line, describing an operation 1.

If type = 2, there will be 2 more integers l, r (1 ≤ l ≤ r ≤ n) in this line, describing an operation 2.

Output

For each operation 2, print a line containing the answer — sum of colorfulness.

Sample Input

Input

3 3
1 1 2 4
1 2 3 5
2 1 3

Output

8

Input

3 4
1 1 3 4
2 1 1
2 2 2
2 3 3

Output

3
2
1

Input

10 6
1 1 5 3
1 2 7 9
1 10 10 11
1 3 8 12
1 1 10 3
2 1 10

Output

129

Hint

In the first sample, the color of each unit is initially [1, 2, 3], and the colorfulness is [0, 0, 0].

After the first operation, colors become [4, 4, 3], colorfulness become [3, 2, 0].

After the second operation, colors become [4, 5, 5], colorfulness become [3, 3, 2].

So the answer to the only operation of type 2 is 8.

线段树成段更新

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std ;

 #define ls ( o << 1 )
 #define rs ( o << 1 | 1 )
 #define lson ls , l , m
 #define rson rs , m + 1 , r
 #define rt o , l , r
 #define root 1 , 1 , n
 #define mid ( ( l + r ) >> 1 )
 #define clear( a , x ) memset ( a , x , sizeof a )

 typedef long long LL ;

 const int MAXN =  ;

 int set[MAXN << ] ;
 LL sum[MAXN << ] ;
 LL add[MAXN << ] ;

 void pushUp ( int o , int l , int r ) {
     set[o] = ( set[ls] == set[rs] ? set[ls] :  ) ;
     sum[o] = sum[ls] + sum[rs] ;
 }

 void pushDown ( int o , int l , int r ) {
     int m = mid ;
     if ( set[o] ) set[ls] = set[rs] = set[o] ;
     if ( add[o] ) {
         sum[ls] += add[o] * ( m - l +  ) ;
         add[ls] += add[o] ;
         sum[rs] += add[o] * ( r - m ) ;
         add[rs] += add[o] ;
         add[o] =  ;
     }
 }

 void build ( int o , int l , int r ) {
     add[o] = set[o] = sum[o] =  ;
     if ( l == r ) {
         set[o] = l ;
         return ;
     }
     int m = mid ;
     build ( lson ) ;
     build ( rson ) ;
 }

 void update ( int x , int L , int R , int o , int l , int r ) {
     if ( L <= l && r <= R ) {
         if ( set[o] ) {
             add[o] += abs ( x - set[o] ) ;
             sum[o] += ( LL ) abs ( x - set[o] ) * ( r - l +  ) ;
             set[o] = x ;
             return ;
         }
     }
     pushDown ( rt ) ;
     int m = mid ;
     if ( L <= m ) update ( x , L , R , lson ) ;
     if ( m <  R ) update ( x , L , R , rson ) ;
     pushUp ( rt ) ;
 }

 LL query ( int L , int R , int o , int l , int r ) {
     if ( L <= l && r <= R ) return sum[o] ;
     pushDown ( rt ) ;
     int m = mid ;
     LL ans =  ;
     if ( L <= m ) ans += query ( L , R , lson ) ;
     if ( m <  R ) ans += query ( L , R , rson ) ;
     return ans ;
 }

 void work () {
     int n , m ;
     int type , l , r , x ;
     while ( ~scanf ( "%d%d" , &n , &m ) ) {
         build ( root ) ;
         while ( m -- ) {
             scanf ( "%d%d%d" , &type , &l , &r ) ;
             if ( type ==  ) {
                 scanf ( "%d" , &x ) ;
                 update ( x , l , r , root ) ;
             }
             else printf ( "%I64d\n" , query ( l , r , root ) ) ;
         }
     }
 }

 int main () {
     work () ;
     return  ;
 }

DZY Loves Chessboard

Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-07-08)

Description

DZY loves chessboard, and he enjoys playing with it.

He has a chessboard of n rows and m columns. Some cells of the chessboard are bad, others are good. For every good cell, DZY wants to put a chessman on it. Each chessman is either white or black. After putting all chessmen, DZY wants that no two chessmen with the same color are on two adjacent cells. Two cells are adjacent if and only if they share a common edge.

You task is to find any suitable placement of chessmen on the given chessboard.

Input

The first line contains two space-separated integers n and m(1 ≤ n, m ≤ 100).

Each of the next n lines contains a string of m characters: the j-th character of the i-th string is either "." or "-". A "." means that the corresponding cell (in the i-th row and the j-th column) is good, while a "-" means it is bad.

Output

Output must contain n lines, each line must contain a string of m characters. The j-th character of the i-th string should be either "W", "B" or "-". Character "W" means the chessman on the cell is white, "B" means it is black, "-" means the cell is a bad cell.

If multiple answers exist, print any of them. It is guaranteed that at least one answer exists.

Sample Input

Input

1 1
.

Output

B

Input

2 2
..
..

Output

BW
WB

Input

3 3
.-.
---
--.

Output

B-B
---
--B

Hint

In the first sample, DZY puts a single black chessman. Of course putting a white one is also OK.

In the second sample, all 4 cells are good. No two same chessmen share an edge in the sample output.

In the third sample, no good cells are adjacent. So you can just put 3 chessmen, no matter what their colors are.

先暴力出一个相邻都不同颜色的表，'.'根据表输出结果，'-'直接输出'-'。

#include<stdio.h>
#define maxn 109
int map[maxn][maxn];

void init()
{
    int i,j,t;
    for(i = ;i<maxn;i++)
    {
        if(i%) t=;
        else t=;
        for(j=;j<maxn;j++)
        {
            map[i][j]=t;
            t=!t;
        }
    }
}
int main()
{
    int i,j;
    init();
    int n,m;
    char ss;
    while(~scanf("%d %d",&n,&m))
    for(i = ;i<n;i++)
    {
      getchar();
        for(j=;j<m;j++)
        {

        ss=getchar();
        if(ss == '-')
            printf("-");
        else
            printf("%c",map[i][j]?'B':'W');
        }
        printf("\n");
    }
    return ;
}

DZY Loves Chemistry

Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-07-09)

Description

DZY loves chemistry, and he enjoys mixing chemicals.

DZY has n chemicals, and m pairs of them will react. He wants to pour these chemicals into a test tube, and he needs to pour them in one by one, in any order.

Let's consider the danger of a test tube. Danger of an empty test tube is 1. And every time when DZY pours a chemical, if there are already one or more chemicals in the test tube that can react with it, the danger of the test tube will be multiplied by 2. Otherwise the danger remains as it is.

Find the maximum possible danger after pouring all the chemicals one by one in optimal order.

Input

The first line contains two space-separated integers n and m.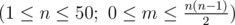

Each of the next m lines contains two space-separated integers x_i and y_i(1 ≤ x_i < y_i ≤ n). These integers mean that the chemical x_iwill react with the chemical y_i. Each pair of chemicals will appear at most once in the input.

Consider all the chemicals numbered from 1 to n in some order.

Output

Print a single integer — the maximum possible danger.

Sample Input

Input

1 0

Output

1

Input

2 1
1 2

Output

2

Input

3 2
1 2
2 3

Output

4
题目大意：有n种化学物质跟m种反应关系，试管初始的危险系数为1，每次往试管中添加物质，若与前面的物质发生了化学反应那么危险系数乘以2，求最大危险系数。
解题思路：用并查集找出各个集合，每个结合的最大发生反应次数为它物质的个数-1。换种思路，就是求s=物质的总数-集合个数,结果为2^t。

 #include<stdio.h>
 #define maxn 105
 typedef long long LL;
 int fa[maxn];
 int find(int x)
 {
     while(fa[x] != x)
     {
         x = fa[x];
     }
     return x;
 }
 void merge(int x,int y)
 {
     int a = find(x);
     int b = find(y);
     if(a != b)
         fa[a] = b;
 }

 int main()
 {
     int n,m,i,a,b;
     scanf("%d%d",&n,&m);
     for(i=;i<maxn;i++)
         fa[i] = i;
     for(i = ;i<m;i++)
     {
         scanf("%d%d",&a,&b);
         merge(a,b);
     }
     int t=;
     LL ans =;
     for(i = ;i<=n;i++)
     {
         if(fa[i] == i)t++;
     }
     ans = ans<<(n-t);
     printf("%lld\n",ans);
     return ;
 }

DZY Loves Modification

Time Limit:2000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-07-14)

Description

As we know, DZY loves playing games. One day DZY decided to play with a n × m matrix. To be more precise, he decided to modify the matrix with exactly k operations.

Each modification is one of the following:

1. Pick some row of the matrix and decrease each element of the row by p. This operation brings to DZY the value of pleasure equal to the sum of elements of the row before the decreasing.
2. Pick some column of the matrix and decrease each element of the column by p. This operation brings to DZY the value of pleasure equal to the sum of elements of the column before the decreasing.

DZY wants to know: what is the largest total value of pleasure he could get after performing exactly k modifications? Please, help him to calculate this value.

Input

The first line contains four space-separated integers n, m, k and p(1 ≤ n, m ≤ 10³; 1 ≤ k ≤ 10⁶; 1 ≤ p ≤ 100).

Then n lines follow. Each of them contains m integers representing a_ij (1 ≤ a_ij ≤ 10³) — the elements of the current row of the matrix.

Output

Output a single integer — the maximum possible total pleasure value DZY could get.

Sample Input

Input

2 2 2 2
1 3
2 4

Output

11

Input

2 2 5 2
1 3
2 4

Output

11

Hint

For the first sample test, we can modify: column 2, row 2. After that the matrix becomes:

1 1
0 0

For the second sample test, we can modify: column 2, row 2, row 1, column 1, column 2. After that the matrix becomes:

-3 -3
-2 -2

题目大意：一个n*m的矩阵有k次操作,每次操作选一行或一列同时减去p操作的价值为这一行或一列没操作之前的和,求最大的价值。
解题思路：一共操作k次，可以设行操作i次,列操作k-i次，每次都是最优操作即选那一行或那一列的和最大的，对i从0到k枚举结果。

 #include <iostream>
 #include <cstdio>
 #include <queue>
 #include <cstring>
 using namespace std;

 typedef __int64 LL;
 const int maxn=;
 const int maxm=;
 int map[maxn][maxn];
 LL C[maxm],R[maxm];
 priority_queue<LL>sc,sr;
 LL max(LL a,LL b){return a>b?a:b;}

 int main()
 {
     int i,j,n,m,k,p;
     LL ans,s;
     while(~scanf("%d %d %d %d",&n,&m,&k,&p))
     {
         while(!sc.empty()) sc.pop();
         while(!sr.empty()) sr.pop();
         memset(C,,sizeof(C));
         memset(R,,sizeof(R));
         for(i=;i<n;i++)
         for(j=;j<m;j++)
             scanf("%d",&map[i][j]);
         for(i=;i<n;i++)
         {
             s=;
             for(j=;j<m;j++)
                 s+=map[i][j];
             sc.push(s);
         }
         for(j=;j<m;j++)
         {
             s=;
             for(i=;i<n;i++)
                 s+=map[i][j];
             sr.push(s);
         }
         for(i=;i<=k;i++)
         {
             s=sc.top();sc.pop();
             C[i]=C[i-]+s;
             s=s-p*m;
             sc.push(s);
         }
         for(i=;i<=k;i++)
         {
             s=sr.top();sr.pop();
             R[i]=R[i-]+s;
             s=s-p*n;
             sr.push(s);
         }
         ans=-1e18;
         for(i=;i<=k;i++)
             ans=max(ans,C[i]+R[k-i]-(LL)i*(k-i)*p);
         printf("%I64d\n",ans);
     }
     return ;
 }

Artem and Array

Time Limit:2000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-06-20)

Description

Artem has an array of n positive integers. Artem decided to play with it. The game consists of n moves. Each move goes like this. Artem chooses some element of the array and removes it. For that, he gets min(a, b) points, where a and b are numbers that were adjacent with the removed number. If the number doesn't have an adjacent number to the left or right, Artem doesn't get any points.

After the element is removed, the two parts of the array glue together resulting in the new array that Artem continues playing with. Borya wondered what maximum total number of points Artem can get as he plays this game.

Input

The first line contains a single integer n(1 ≤ n ≤ 5·10⁵) — the number of elements in the array. The next line contains n integers a_i(1 ≤ a_i ≤ 10⁶) — the values of the array elements.

Output

In a single line print a single integer — the maximum number of points Artem can get.

Sample Input

Input

5
3 1 5 2 6

Output

11

Input

5
1 2 3 4 5

Output

6

Input

5
1 100 101 100 1

Output

102

题目大意：给一个n的整数序列，每次删除一个数此次操作的价值为它左右两个数间的较小值，若左边或右边没有数那此次操作的价值为0，求最大价值。
解题思路：本着这波不亏的贪心思想，先从那些删了这个数不亏的开始，即左右两个数均大于等于它。当这样的好事做完后，新序列有三种情况（1）单调递增（2）单调递减（3）先增后减。这种情况价值最大的情况为序列和减去最大的两个数（绝对不坑）。

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 inline int min(int a,int b){ return a<b?a:b;}
 const int maxn=;
 int n,f[maxn];

 int main()
 {
     int i,top,x;
     LL ans;
     while(~scanf("%d",&n))
     {
         ans=;top=;
         for(i=;i<n;i++)
         {
             scanf("%d",&x);
             while(top>&&f[top-]>=f[top-]&&x>=f[top-])
             {
                 ans+=min(x,f[top-]);
                 top--;
             }
             f[top++]=x;
         }
         sort(f,f+top);
         for(i=;i<top-;i++) ans+=f[i];
         printf("%lld\n",ans);
     }
     return ;
 }