BZOJ2395 [Balkan 2011]Timeismoney 【最小乘积生成树】

题目链接

BZOJ2395

题意：无向图中每条边有两种权值，定义一个生成树的权值为两种权值各自的和的积

求权值最小的生成树

题解

如果我们将一个生成树的权值看做坐标，那么每一个生成树就对应一个二维平面上的坐标

在同一个反比例函数图像上的点权值相同，反比例函数\(xy\)越小的点越贴近坐标轴

所以答案一定在下凸包上

我们就递归查找这样的点

我们先分别将两种权值作为指标求出\(A\)和\(B\)两个点，分别是\(x\)最小的点和\(y\)最小的点，即为下凸包的一个边界

我们找到位于\(AB\)左下角最远的点\(C\)

为了方便，由于底\(|AB|\)确定，\(S\triangle ABC\)越大，距离越远

那么\(C\)满足最小化

\[\overrightarrow{CA} \times \overrightarrow{CB}
\]

展开叉乘，去掉常数项，可得

\[(y_A - y_B) * x_C + (x_B - x_A) * y_C
\]

将其作为新的边权，跑kruskal即可得到新的点\(C\)

然后将\(AC\)和\(CB\)分别作为底继续递归下去，直至找不到点为止

过程中更新答案，显然一定会经过下凸包上所有点

复杂度\(O(可以被卡)\)，只需要构造所有点都在下凸包上，就会退化为\(O(生成树个数)\)

不知道能不能构造出来

为了方便理解，再盗一张图

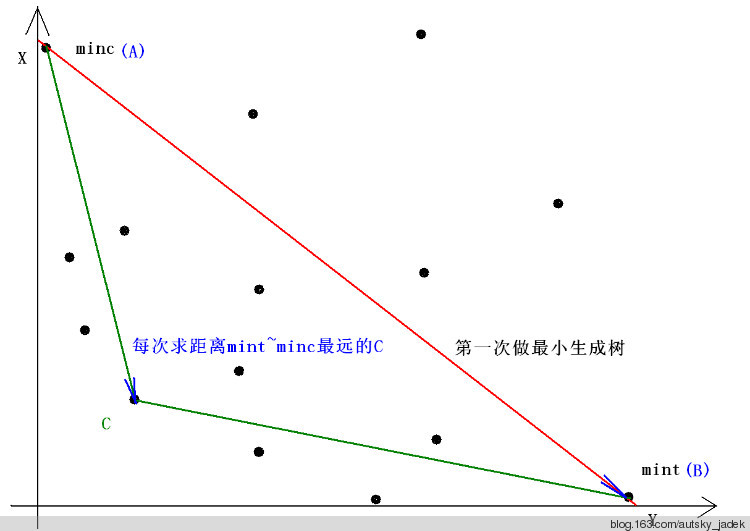
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 205,maxm = 10005,INF = 0x3fffffff;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int n,m,pre[maxn];
struct EDGE{int a,b,x,y,v;}e[maxm];
struct point{int x,y;}ans;
inline int find(int u){return u == pre[u] ? u : pre[u] = find(pre[u]);}
inline bool operator <(const EDGE& a,const EDGE& b){
	return a.v < b.v;
}
inline point operator -(const point& a,const point& b){
	return (point){a.x - b.x,a.y - b.y};
}
inline LL operator *(const point& a,const point& b){
	return 1ll * a.x * b.y - 1ll * a.y * b.x;
}
inline bool operator <(const point& a,const point& b){
	return 1ll * a.x * a.y == 1ll * b.x * b.y ? a.x < b.x : 1ll * a.x * a.y < 1ll * b.x * b.y;
}
point kruskal(){
	sort(e + 1,e + 1 + m);
	REP(i,n) pre[i] = i;
	point re; int cnt = n,u,v; re.x = re.y = 0;
	for (int i = 1; i <= m && cnt > 1; i++){
		u = find(e[i].a); v = find(e[i].b);
		if (u != v){
			pre[u] = v;
			cnt--;
			re.x += e[i].x;
			re.y += e[i].y;
		}
	}
	if (re < ans) ans = re;
	return re;
}
void solve(point A,point B){
	REP(i,m) e[i].v = (A.y - B.y) * e[i].x + (B.x - A.x) * e[i].y;
	point C = kruskal();
	if ((C - A) * (B - A) <= 0) return;
	solve(A,C); solve(C,B);
}
int main(){
	n = read(); m = read(); ans.x = ans.y = INF;
	REP(i,m){
		e[i].a = read() + 1,e[i].b = read() + 1;
		e[i].x = read(),e[i].y = read();
	}
	REP(i,m) e[i].v = e[i].x;
	point A = kruskal();
	REP(i,m) e[i].v = e[i].y;
	point B = kruskal();
	solve(A,B);
	printf("%d %d\n",ans.x,ans.y);
	return 0;
}