《剑指offer》数学题及其它 (牛客11.05)

比较多的思维题，涉及位运算、快速幂、二进制、约瑟夫问题、队列、贪心、dp等等。

难度	题目	知识点
☆	12、数值的整数次方	细节，快速幂
☆☆	47、求1+2+3+···+n	思维发散
☆☆	48、不用加减乘除做加法	二进制运算
☆☆☆	11、二进制中1的个数	补码，位运算
☆☆☆☆	29、最小的K个数	查找第K大，或各种排序算法
☆	31、从1到n整数中1出现的次数	思维
☆	33、丑数	思维
	41、和为S的连续正数序列	滑动窗口，双指针
	42、和为S的两个数字	滑动窗口，双指针
	45、扑克牌顺子	多种情况判断
☆☆☆	46、圆圈中最后剩下的数	约瑟夫环，数学
☆☆☆	63、数据流中的中位数	妙用堆，PriorityQueue
☆☆☆	64、滑动窗口的最大值	模拟，滑动窗口，双端队列
☆☆☆	67、剪绳子	贪心，动态规划

12、数值的整数次方+

细节，快速幂

给定一个double类型的浮点数 base 和 int 类型的整数exponent。求base的exponent次方。 保证base和exponent不同时为0

题意分析

指数可能为负数。

Java Code

class Solution {
public:
    double Power(double base, int exponent) {
        double ans=1;
        bool neg= false;
        if(exponent

47、求1+2+3+···+n ++

思维发散

求1+2+3+...+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

题意分析

需要思维发散，善用递归和短路运算，见代码。

Java Code

class Solution {
public:
    int Sum_Solution(int n) {
        int ans = n;
        ans && (ans += Sum_Solution(n - 1));
        return ans;
    }
};

48、不用加减乘除做加法++

二进制运算

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

题意分析

第一步：相加各位的值，不算进位，得到010，二进制每位相加就相当于各位做异或操作，101^111。

第二步：计算进位值，得到1010，相当于各位做与操作得到101，再向左移一位得到1010，(101&111)<<1。 第三步：重复上述两步， 各位相加 010^1010=1000，进位值为100=(010&1010)<<1。

继续重复上述两步：1000^100 = 1100，进位值为0，跳出循环，1100为最终结果。

注意循环终止条件。 有负数相加的情况。

Java Code

class Solution {
public:
    int Add(int num1, int num2)
    {
        while(num2!=0){
            int tmp=num1^num2;
            num2=(num1 & num2)

---

11、二进制中1的个数 ++

补码，位运算

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

题意分析

注意对于负数，右移一位会补 1 而非补零。

CPP Code

// 1. 去掉符号位 1
class Solution {
public:
     int  NumberOf1(int n) {
         int cnt=0;
         if(n>=1;
         }
         return cnt;
     }
};
// 2. 转为 unsigned int
class Solution {
public:
     int  NumberOf1(int n) {
         unsigned int nn=n;
         int cnt=0;
         while(nn){
             cnt+=(nn&1);
             nn>>=1;
         }
         return cnt;
     }
};
// 3. 每次 n&(n-1) 将从右边起的第一个 1 变为 0
public class Solution {
    public int NumberOf1(int n) {
        int count = 0;
        while(n!= 0){
            count++;
            n = n & (n - 1);
         }
        return count;
    }
}

29、最小的K个数+++

查找第K大，或各种排序算法

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

题意分析

用Partition O(n)找到第K大。然后遍历输出前K个数。

• 检查数据合法情况
• partition编写
• 不用IDE的话出现了全角字符、忘记导入包的问题

Java Code

import java.util.Arrays;
import java.util.ArrayList;
public class Solution {
    public ArrayList GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList ans=new ArrayList();
        if(input==null|| k==0 || k>input.length) return ans;
        int x=k+1,st=0,ed=input.length-1;
        do{
            x=Partition(input,st,ed);
            if(xk-1){ed=x-1;}
        }while(x!=k-1);
        //Arrays.sort(input,0,k);
        for(int i=0;i  i && arr[j] >= pivot)j--;
            arr[i]=arr[j];
            while(i 

31、从1到n整数中1出现的次数++++

思维

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

题意分析

将n的各个位分为两类：个位与其它位。

对个位来说：

• 若个位大于0，1出现的次数为round*1+1
• 若个位等于0，1出现的次数为round*1

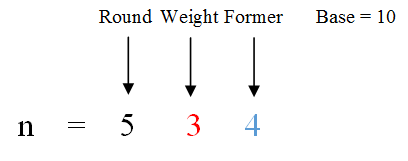
对其它位来说，记每一位的权值为base，位值为weight，该位之前的数是former，举例如图：

则：

• 若weight为0，则1出现次数为round*base
• 若weight为1，则1出现次数为round*base+former+1
• 若weight大于1，则1出现次数为rount*base+base

比如：

534 = （个位1出现次数）+（十位1出现次数）+（百位1出现次数）
	=（53*1+1）+（5*10+10）+（0*100+100）= 214
530 = （53*1）+（5*10+10）+（0*100+100） = 213
504 = （50*1+1）+（5*10）+（0*100+100） = 201
514 = （51*1+1）+（5*10+4+1）+（0*100+100） = 207
10 = (1*1)+(0*10+0+1) = 2

————————————————

版权声明：本文为CSDN博主「yi_afly」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/yi_afly/article/details/52012593

Java Code

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        int base=1,round=n,weight,former;
        int cnt=0;
        while(base  1)cnt+=base;
            base*=10;
        }
        return cnt;
    }
}

33、丑数 +

思维

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

题意分析

根据丑数的定义，丑数应该是另一个丑数乘以2、3或者5的结果（1除外）。因此，我们可以创建一个数组，里面保存的是排好序的丑数，每一个丑数都可以由前面的丑数乘以2、3或者5得到。

问题在于，如何保证生成的丑书序列是有序的。解决方法是，维护3个“指针”，分别指向2、3、5当前要乘的数，然后取三个乘积中的最小加入丑数序列，同时，维护指针所指位置。要注意的是，为了避免重复，如果出现minn==2*num[p2]==5*nums[p5]的情况，那么两个指针都需要后移。

• 细节 - 重复不计

Java Code

import java.util.ArrayList;
public class Solution {
    public int GetUglyNumber_Solution(int index) {
        if (index  nums = new ArrayList();
        nums.add(1);
        int p2 = 0, p3 = 0, p5 = 0;
        while (cnt 

41、和为S的连续正数序列

滑动窗口，双指针

题目描述

小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!

输出描述:

输出所有和为S的连续正数序列。序列内按照从小至大的顺序，序列间按照开始数字从小到大的顺序

题意分析

n从1开始递增，长度从sum开始递减，检查是否满足序列和为sum。

• 审题 - 序列长大于1

Java Code

import java.util.ArrayList;
public class Solution {
    public ArrayList> FindContinuousSequence(int sum) {
        ArrayList> ans = new ArrayList();
        ArrayList cur;
        if (sum  1) {
            while ((n + n + l - 1) * l / 2 > sum) l--;
            if (l > 1 && (n + n + l - 1) * l / 2 == sum) {
                cur = new ArrayList();
                for (int i = n; i 

42、和为S的两个数字

滑动窗口，双指针

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

输出描述:

对应每个测试案例，输出两个数，小的先输出。

题意分析

和上题类似的滑动窗口，双指针。

Java Code

import java.util.ArrayList;
public class Solution {
    public ArrayList FindNumbersWithSum(int[] array, int sum) {
        ArrayList ans = new ArrayList();
        if (array == null || array.length  sum && p1 

45、扑克牌顺子

多种情况判断

题目描述

LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张^_)...他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿！！“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子.....LL不高兴了,他想了想,决定大\小 王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。 现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何， 如果牌能组成顺子就输出true，否则就输出false。为了方便起见,你可以认为大小王是0。

题意分析

有四张王一定为顺子，其余情况下，一副牌为顺子当且仅当最大数字牌和最小数字牌之差小于5且没有重复的数字牌。

• 输入数据检查
• 数组边界

Java Code

import java.util.Arrays;
public class Solution {
    public boolean isContinuous(int[] numbers) {
        if (numbers == null || numbers.length != 5) return false;
        Arrays.sort(numbers);
        int minn = 0, maxx = numbers[numbers.length - 1];
        int loc = -1;
        for (int i = 0; i  0) {
                loc = i;
                minn = numbers[i];
                break;
            }
        }
        if (loc == numbers.length - 1) return true;// 4 king
        if (maxx - minn + 1 > 5) return false;
        for (int i = loc; i + 1 

46、圆圈中最后剩下的数+++

约瑟夫环，数学

题目描述

每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_)。请你试着想下,哪个小朋友会得到这份礼品呢？(注：小朋友的编号是从0到n-1)

如果没有小朋友，请返回-1

题意分析

用模拟来做自然是可以的。但复杂度是O(n*m)。看了一下别人的数学推导思路。

原问题是从0...n-1中循环去掉第m个数，求剩下的最后一个数是多少，我们假设原求解问题是f(n,m)。

去掉第一个数k=(m-1)%n之后，还剩下k+1...n-1,0...k-1这n-1个数，问题变成了从这n-1个数中循环删去第m个数，求最后剩下的一个数，记这个问题为f'(n-1,m)。那么f(n,m)与f'(n-1,m)最终得到的结果是相同的，即①f(n,m)=f'(n-1,m)。

而如果把k+1...n-1,0...k-1与0..n-1作置换，那么②f'(n-1,m)=(f(n-1,m)+k+1)%n，①②式联合，得到f(n,m)=(f(n-1,m)+k+1)%n。于是递归关系就找到了，这样计算的时间复杂度是O(n)。

最后注意递归的出口，见代码。

Java Code

public class Solution {
    public int LastRemaining_Solution(int n, int m) {
        if (n == 0) return -1;
        if (n == 1) return 0;
        return (LastRemaining_Solution(n - 1, m) + m) % n;
    }
}

63、数据流中的中位数+++

妙用堆，PriorityQueue

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

题意分析

gzshan的分析很清晰。

方法五：最大堆和最小堆。我们注意到当数据保存到容器中时，可以分为两部分，左边一部分的数据要比右边一部分的数据小。如下图所示，P1是左边最大的数，P2是右边最小的数，即使左右两部分数据不是有序的，我们也有一个结论就是：左边最大的数小于右边最小的数。

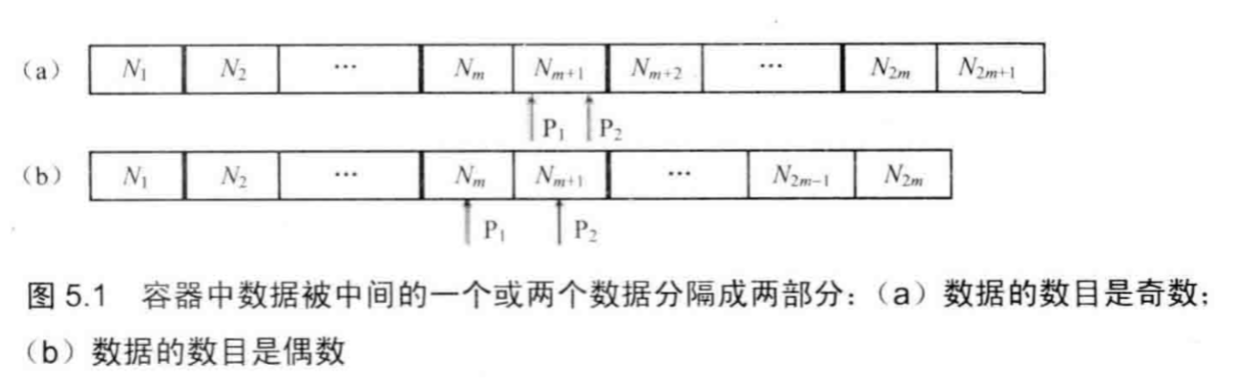
因此，我们可以有如下的思路：向堆中插入一个数据的时间是O(logn)，而中位数就是堆顶的数据，只需要O(1)的时间就可得到。

而在具体实现上，首先要保证数据平均分配到两个堆中，两个堆中的数据数目之差不超过1，为了实现平均分配，可以在数据的总数目是偶数时，将数据插入最小堆，否则插入最大堆。

此外，还要保证所有最大堆中的数据要小于最小堆中的数据。所以，新传入的数据要和最大堆中最大值或者最小堆中的最小值比较。当总数目是偶数时，我们会插入最小堆，但是在这之前，我们需要判断这个数据和最大堆中的最大值哪个更大，如果最大值中的最大值比较大，那么将这个数据插入最大堆，并把最大堆中的最大值弹出插入最小堆。由于最终插入到最小堆的是原最大堆中最大的，所以保证了最小堆中所有的数据都大于最大堆中的数据。

Java Code

import java.util.Comparator;
import java.util.PriorityQueue;
public class Solution {
    PriorityQueue minQ = new PriorityQueue();// default
    PriorityQueue maxQ = new PriorityQueue(new Comparator() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });
    int cnt = 0;
    public void Insert(Integer num) {
        cnt++;
        if ((cnt & 1) == 1) {
            int candidate = num + 1;
            if (!minQ.isEmpty()) candidate = minQ.peek();
            if (num = candidate) minQ.offer(num);
            else {
                minQ.offer(candidate);
                maxQ.poll();
                maxQ.offer(num);
            }
        }
    }
    public Double GetMedian() {
        if ((cnt & 1) == 1) return (double) maxQ.peek();
        else return (minQ.peek() + maxQ.peek()) / 2.0;
    }
}

64、滑动窗口的最大值+++

模拟，滑动窗口，双端队列

题目描述

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

题意分析

用双端队列，维护队首元素为当前窗口的最大值的下标，队中元素为后续窗口可能的最大值的下标。具体为，每次后移一格成为新的滑动窗口时，【如果队首过期，那么将队首删去】，【如果删掉队列中所有比新元素小的元素】，【再将新元素下标加入】，此时，队首值就是当前窗口的最大值下标。

第一个操作保证及时删掉了过期的最大值。第二个操作保证了队列中都是可能为最大值的元素下标，及时剔除了不可能为最大值的元素。第三个操作是由于随着窗口后移，新的元素可能成为最大元素。

举例

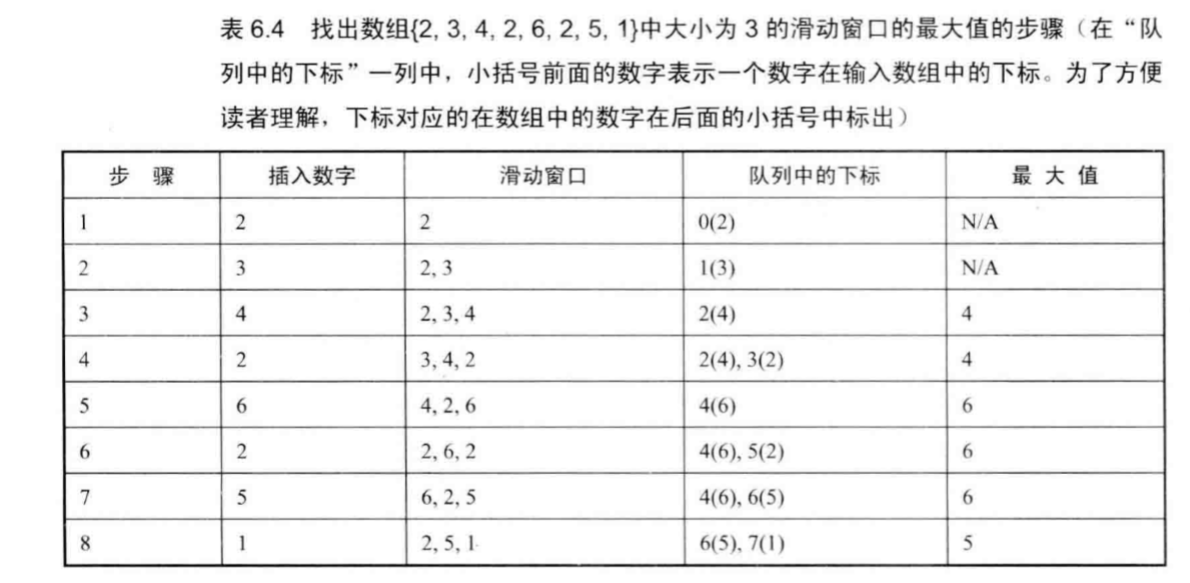
Java Code

import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
public class Solution {
    public ArrayList maxInWindows(int[] num, int size) {
        ArrayList ans = new ArrayList();
        if (num == null || num.length == 0 || size  num.length)
            return ans;
        Deque dq = new LinkedList();// 存的是下标
        for (int i = 0; i = size) dq.pollFirst();
            while (!dq.isEmpty() && num[dq.peekLast()] 

67、剪绳子+++

贪心，动态规划

题目描述

给你一根长度为n的绳子，请把绳子剪成m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

题意分析

方法一 贪心。尽可能分成3*3*3*..*3或2*3*3*...*3或2*2*3*...*3。因为2*2*2<3*3。

方法二 动态规划。dp[i]定义为，长度为i的绳子，分割或者不分割，得到的最大乘积。

Java Code

public class Solution {
    public int cutRope(int target) {
        int[] dp = new int[60 + 5];
        dp[0] = dp[1] = 0;
        dp[2] = 1;
        dp[3] = 2;
        dp[4] = 4;
        if (target