pytorch中的激励函数（详细版）

      初学神经网络和pytorch，这里参考大佬资料来总结一下有哪些激活函数和损失函数（pytorch表示）

     首先pytorch初始化：  

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numoy形式，tensor形式会报错

一：激活函数：

　　1：首先我们得知道为什么需要激活（激励）函数，它其实就是另外一个非线性函数。如果没有激励函数，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限，而且只有线性组合，隐藏层无论多少层其实和只有一层差不（转换为一次的加权计算）。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

　　2：激励函数的性质：

• 非线性： 当激活函数是线性的时候，一个两层的神经网络就可以逼近基本上所有的函数了。但是，如果激活函数是恒等激活函数的时候（即f(x)=x），就不满足这个性质了，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的。
• 可微性： 当优化方法是基于梯度的时候，这个性质是必须的。
• 单调性： 当激活函数是单调的时候，单层网络能够保证是凸函数。
• f(x)≈x： 当激活函数满足这个性质的时候，如果参数的初始化是random的很小的值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要很用心的去设置初始值。
• 输出值的范围： 当激活函数输出值是 有限 的时候，基于梯度的优化方法会更加 稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是 无限 的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的learning rate

3：常用的激活函数　　　

早期研究神经网络主要采用sigmoid函数或者tanh函数，输出有界，很容易充当下一层的输入。近些年Relu函数及其改进型（如Leaky-ReLU、P-ReLU、R-ReLU等）在多层神经网络中应用比较多。下面我们来总结下这些激活函数：

• 3.1单极性 sigmod函数

3.1.1：Sigmoid 是常用的非线性的激活函数，该函数是将取值为 (−∞,+∞)(−∞,+∞) 的数映射到 (0,1)之间，它的数学形式和图像如下：

     

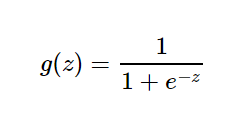
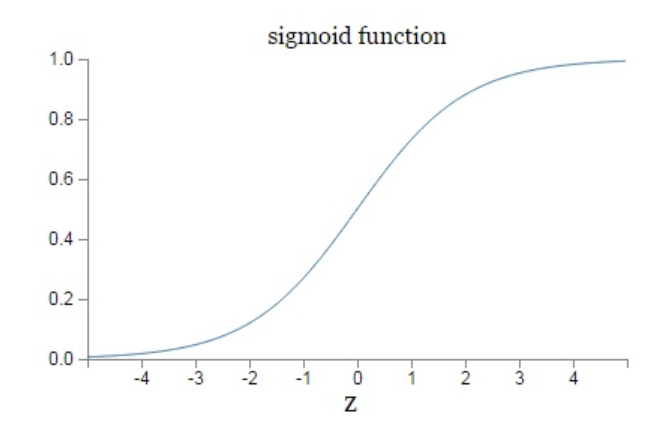
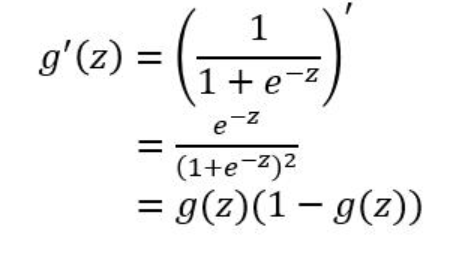
3.1.2：特点：

                    sigmod激励函数符合实际，当输入很小时，输出接近于0；当输入很大时，输出值接近1，但是sigmoid函数作为非线性激活函数，但是其并不被经常使用，它具有以下几个缺点：

1）当 zz 值非常大或者非常小时，通过右上图我们可以看到，sigmoid函数的导数 g′(z)g′(z) 将接近 0 。这会导致权重 WW 的梯度将接近 0 ，使得梯度更新十分缓慢，即梯度消失。

2）非零中心化，也就是当输入为0时，输出不为0，，因为每一层的输出都要作为下一层的输入，而未0中心化会直接影响梯度下降 。

　　　　　　3）计算量比较大。

　　　　sigmoid函数可用在网络最后一层，作为输出层进行二分类，尽量不要使用在隐藏层。　

　　　3.1.3：pytorch实现：

y_sigmoid = F.sigmoid(x).data.numpy()  #初始化已经在上面实现
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')  #图例名称自动选择最佳展示位置
plt.show()  #展示图片和上面（中）类似

• 3.2：双极性tanh函数

3.2.1 :该函数是将取值为 (−∞,+∞)(−∞,+∞) 的数映射到 (−1,1)(−1,1) 之间，其数学形式与图形为：

              

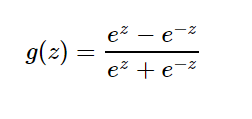
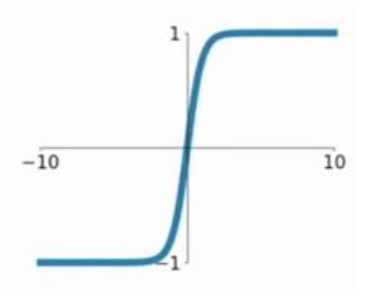
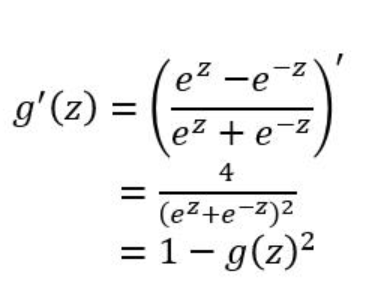
3.2.2：特点：

1）tanh函数在 0 附近很短一段区域内可看做线性的。由于tanh函数均值为 0 ，因此弥补了sigmoid函数均值为 0.5 的缺点。

　　　　　　2）当z为非常大或者非常小的时候，由导数推断公式可知，此时导数接近与0，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

　　　　　　3）幂运算问题仍然存在，计算量比较大。

　　　　3.2.3：pytorch实现：　　　　

y_tanh = F.tanh(x).data.numpy()    #初始化在上面已经给出
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.show()#展示图片和上图（中）相似。

• 3.3：Relu函数

3.3.1 ：又称修正线性单元，是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。ReLU函数的公式以及图形，导数公式如下：

                    

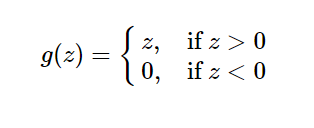
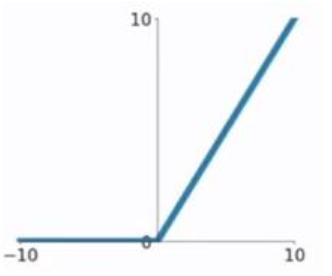
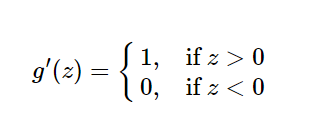
3.3.2：特点：

　　　　1）（1）在输入为正数的时候（对于大多数输入 zz 空间来说），不存在梯度消失问题。
    （2） 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）
   （3）当输入为负时，梯度为0，会产生梯度消失问题

      ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

　　3.3.3：pytorch实现：

y_relu = F.relu(x).data.numpy()
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.show()

• 3.4：Leaky Relu函数

3.4.1：这是一种对ReLU函数改进的函数，又称为PReLU函数，但其并不常用。其公式与图形如下：（a取值在（0，1）之间）

             

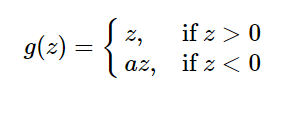
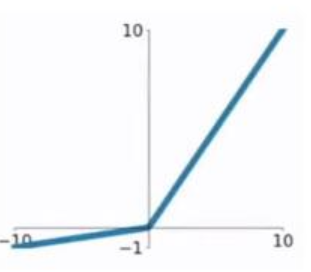
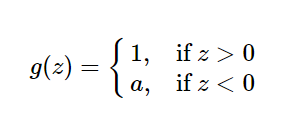
　　　特点：

Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。

　　　　理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

　　3.5：softplus函数

　　　 3.5.1:和relu一样为近似生物神经激活函数，函数数学形式和图像如下：（log里面加1是为了避免非0出现）

                              

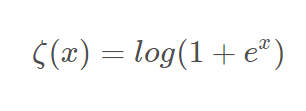
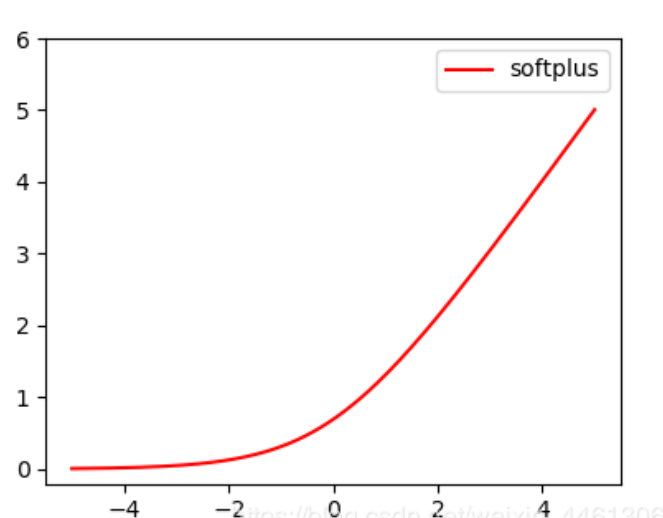
3.5.2：特点：

1）softplus可以看作是ReLu的平滑。

3.5.3：pytorch实现：　　　

y_softplus = F.softplus(x).data.numpy()
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')

plt.show()

4：怎么样去选择激励函数

　　1）在少量层结构中, 我们可以尝试很多种不同的激励函数. 在卷积神经网络 Convolutional neural networks 的卷积层中, 推荐的激励函数是 relu. 在循环神经网络中 recurrent neural networks, 推荐的是 tanh 或者是 relu 。

2）如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.

3）Relu->Lecky Relu/Elu>tanh>sigmoid

5:参考文献：

神经网络中集中激活函数的理解

　 常用激活函数的集合与总结

　神经网络-激励函数

pytorch中常用的激活函数

神经网络激活函数和损失函数的选择