[USACO15FEB]Superbull 超级牛

题意概况

题目描述

\(Bessie\)和她的朋友们正在一年一度的\(Superbull\)锦标赛中打球，而\(Farmer John\)负责让比赛尽可能激动人心。

总共有 \(N\) 支队伍 \(1 \le N \le 2000\) 参加了\(Superbull\)锦标赛。每个团队都有一个 \(1 \dots 2^{30}-1\)的团队ID。

\(Superbull\)是一场淘汰赛 - 在每场比赛之后，\(FJ\)选择淘汰其中一支球队，而被淘汰的球队再也无法参加任何比赛了。当只剩下一支球队时，比赛就结束了。

\(FJ\)注意到一个不寻常的事情：在任何游戏中，两个团队的总分是两个团队ID的按位异或（XOR）。

例如，如果第 \(12\) 队和第 \(20\) 队将参加比赛，则该游戏的得分为 \(24\) 分，因为\({01100} \quad xor \quad {10100} = {11000}\)

FJ想要设计一种比赛方案，让所有比赛的得分总和最大。请帮助\(Farmer John\)组织比赛。

输入输出格式

输入格式：第一行包括一个整数 \(N\) ，下面 \(N\) 行每行包括一个队伍的ID。

输出格式：输出一个整数，代表比赛的最大总得分。

样例解释

让 \(3\) 队与 \(9\) 队进行比赛,并让 \(9\) 队晋级。

然后他让 \(6\) 队和 \(9\) 队对决,让\(6\)队获胜。

最后，第 \(6\) 队和第 \(10\) 队比赛,\(10\)队获胜。

总得分为：\(3 \quad xor \quad 9+6 \quad xor \quad 9+6 \quad xor \quad 10=10+15+12=37。\)

样例输入

4
3
6
9
10

样例输出

37

数据范围

\(1 \le N \le 2000\)

解题报告

题意理解

1. 给定\(n\)个人,比\(n-1\)场比赛

2. 对于一场比赛的精彩度是两个比赛队伍的编号异或

3. 要求所有的比赛的精彩度之和最大.

算法解析

首先,这道题目难在建图上面.

我们可以分析一下,这道题目的比赛模式.

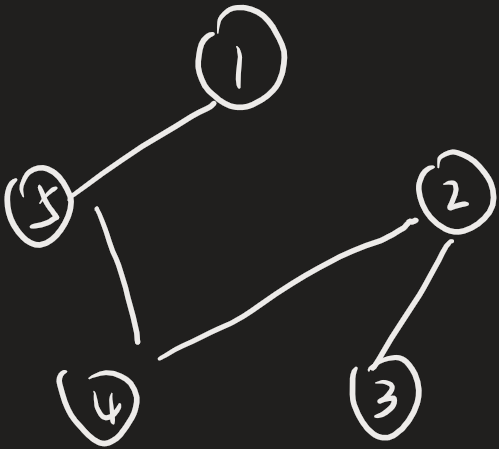
这就是一场竞赛的四场比赛的形式.

我们发现

1. 一共比了\(n-1\)场比赛,有\(n\)个人,呈现,树形结构
2. 对于一场比赛,谁赢谁输并没有什么影响.
3. 我们要求这些边权最大,且只能有\(n-1\)条边
4. 一条边的边权,是两点编号的异或.

综上所述,我们可以使用最小生成树的变形,最大生成树来求解本题.

---

代码解析

#include <bits/stdc++.h>
using namespace std;
const int N=2010;
int a[N],n,m,cnt,fa[N];
struct node
{
	int x,y,w;
} g[N*N];
int cmp(node a,node b)//最大排序
{
	return a.w>b.w;
}
inline int find(int x)
{
	return fa[x]==x?x:fa[x]=find(fa[x]);
}
inline void kruskal()
{
	for(int i=1; i<=n; i++)//建立图
		for(int j=1; j<=n; j++)
			if (i!=j)
				g[++cnt]= {i,j,a[i]^a[j]};//边权为异或
	sort(g+1,g+1+cnt,cmp);//kruskal排序
	int cc=0;
	long long ans=0ll;//记得开long long
	for(int i=1; i<=cnt; i++)
	{
		int x=find(g[i].x),y=find(g[i].y);
		if (x==y)//已经联合
			continue;
		fa[x]=y;
		ans+=g[i].w;
		if (cc==n-1)//n-1条边凑齐了
			break;
	}
	printf("%lld\n",ans);
}
inline void init()
{
	scanf("%d",&n);
	for(int i=1; i<=n; i++)
		scanf("%d",&a[i]),fa[i]=i;
	kruskal();
}
signed main()
{
	init();
	return 0;
}