WEB知识补充 支付宝 支付
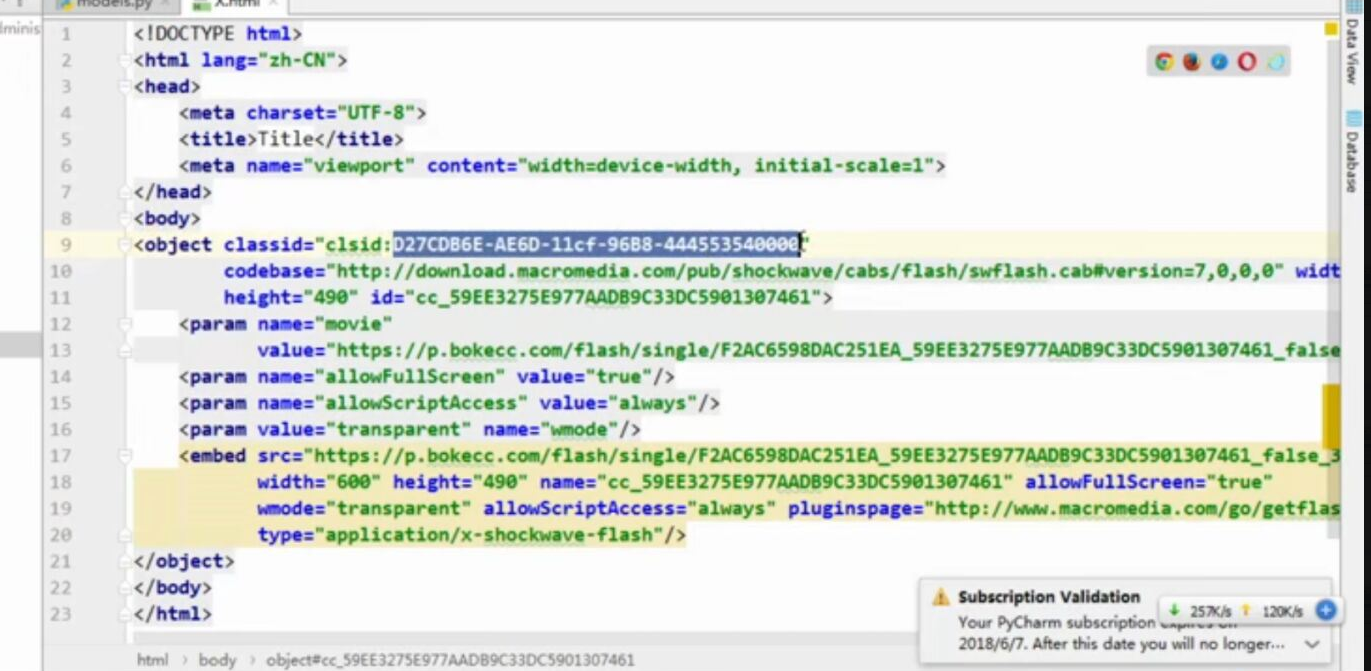
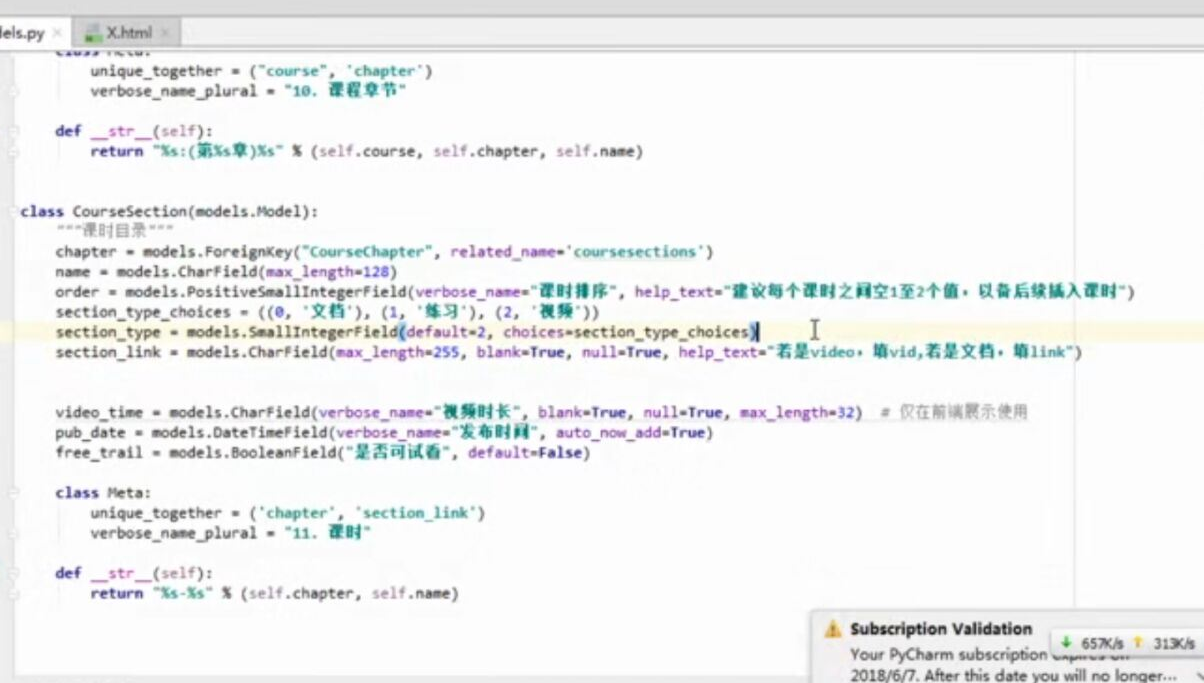
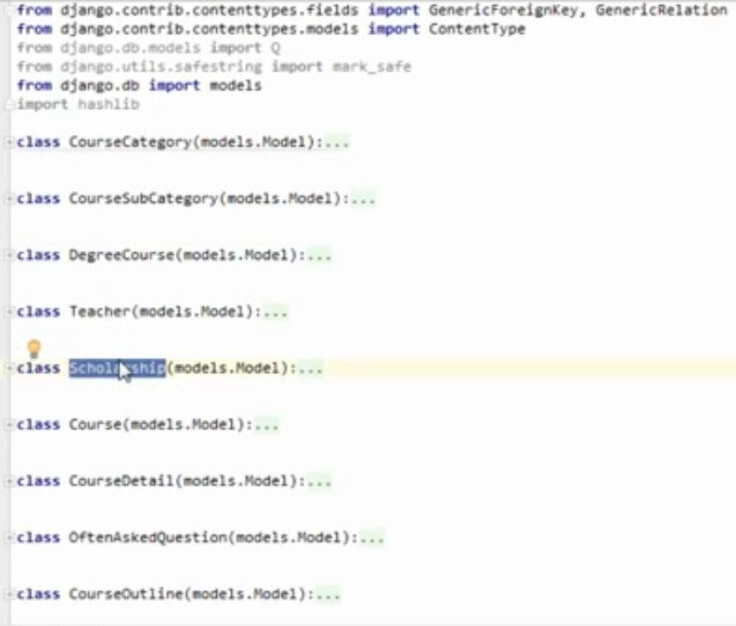
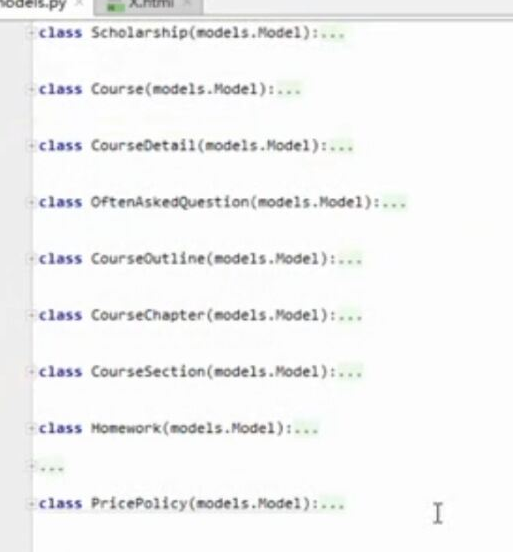
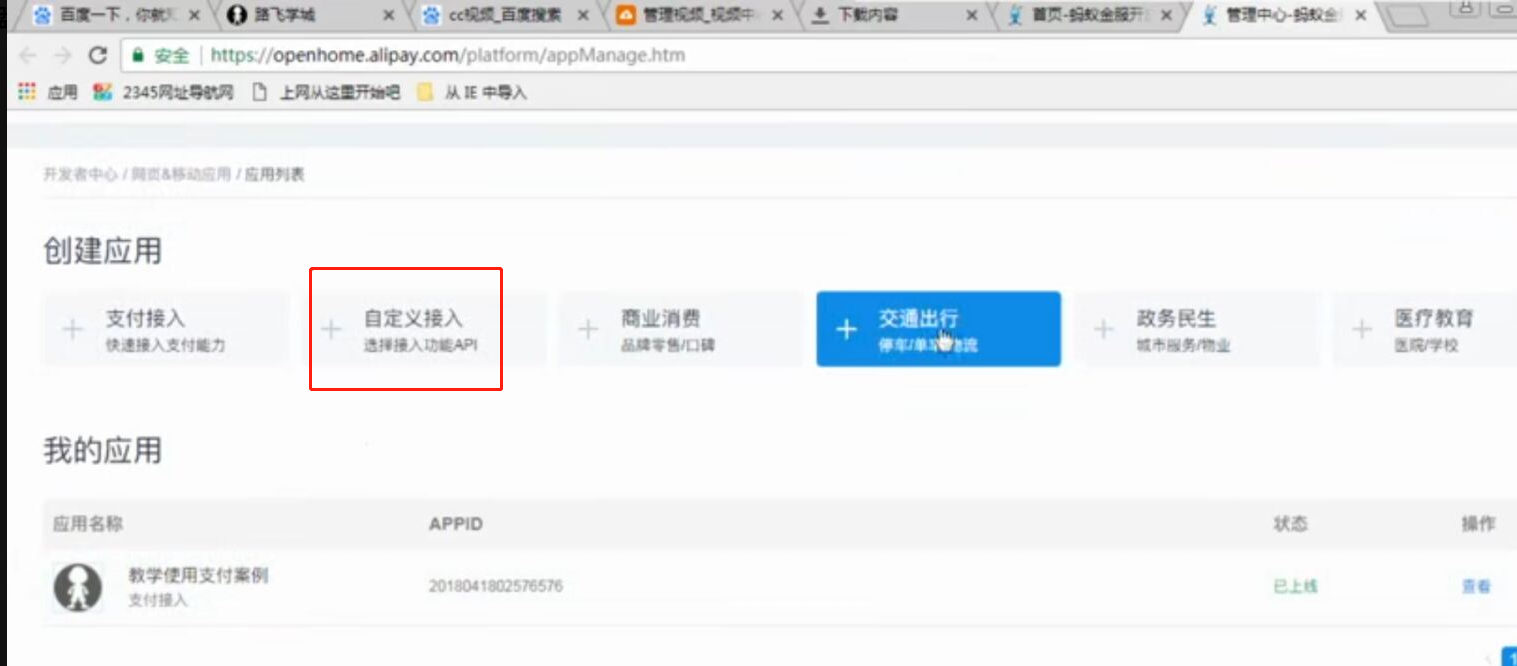
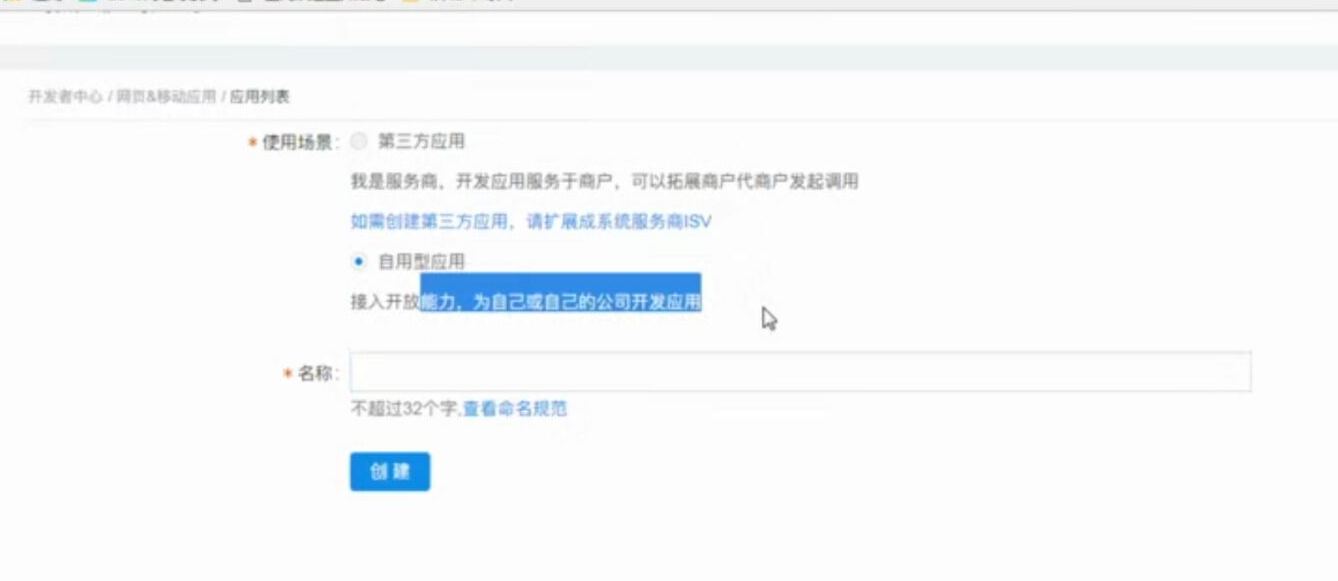
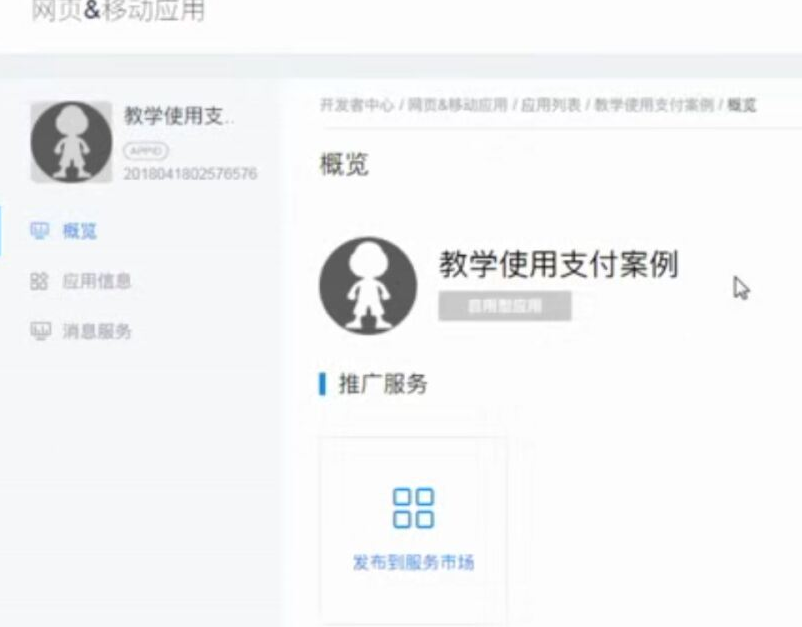
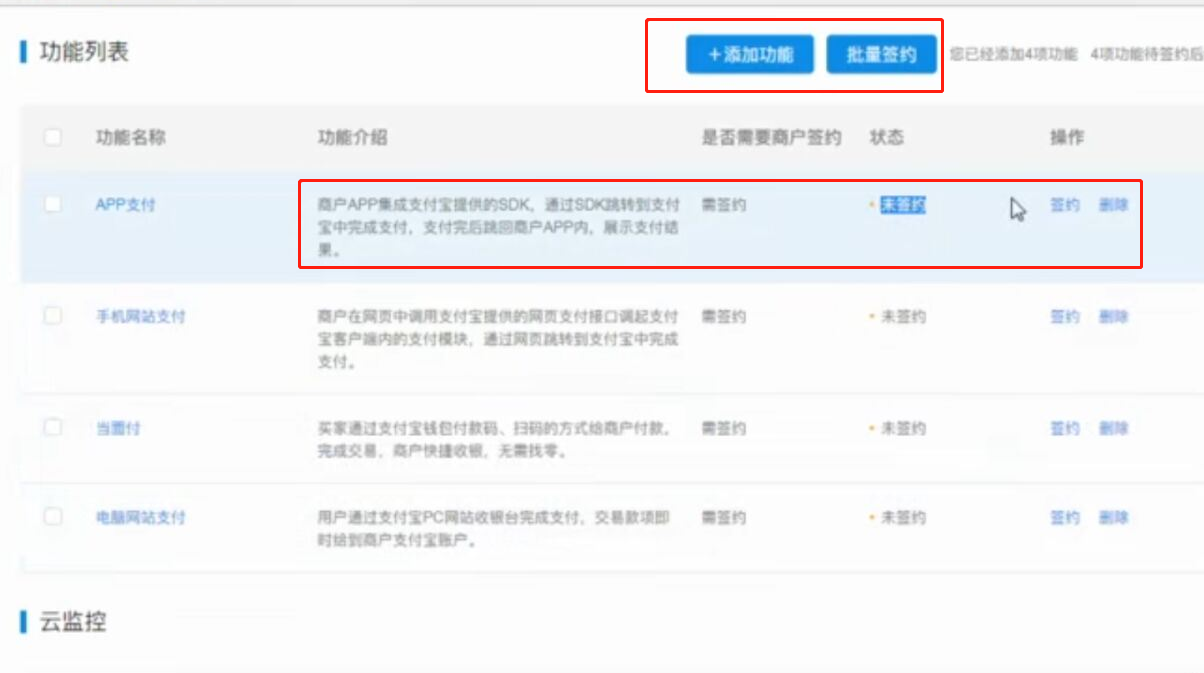


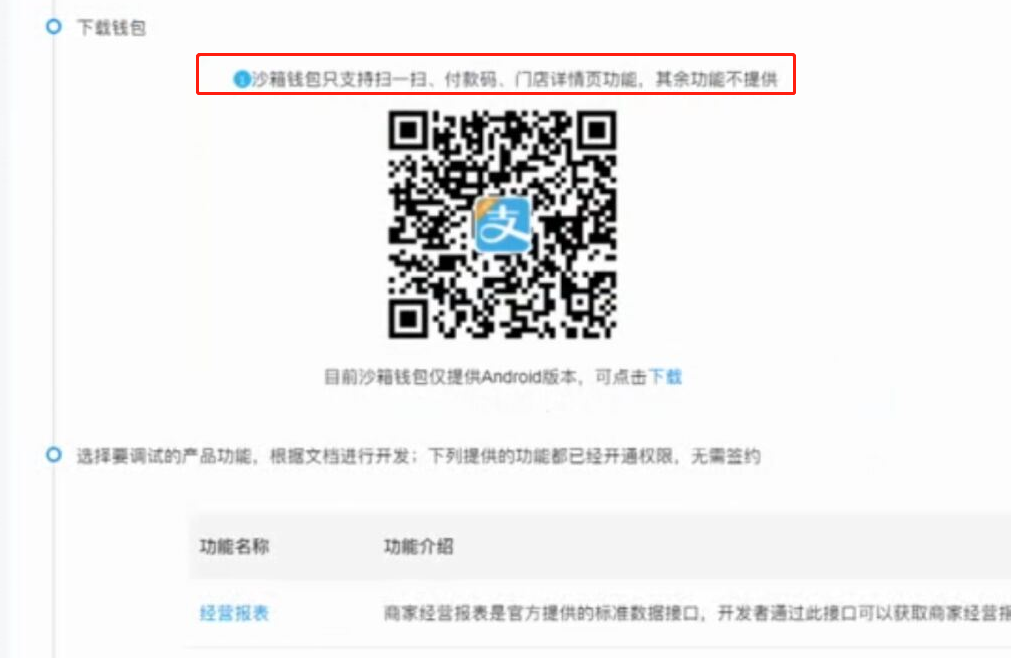
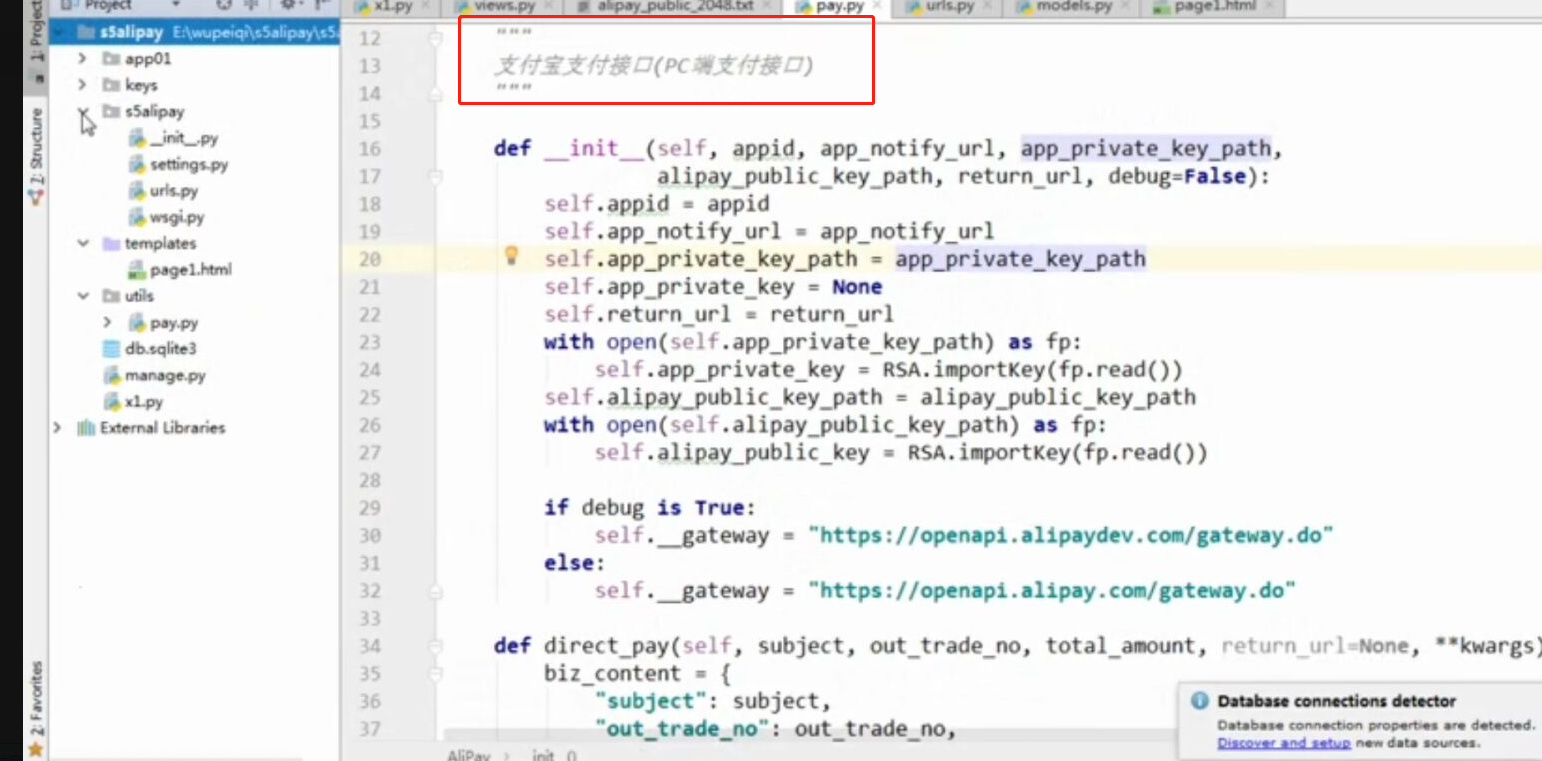
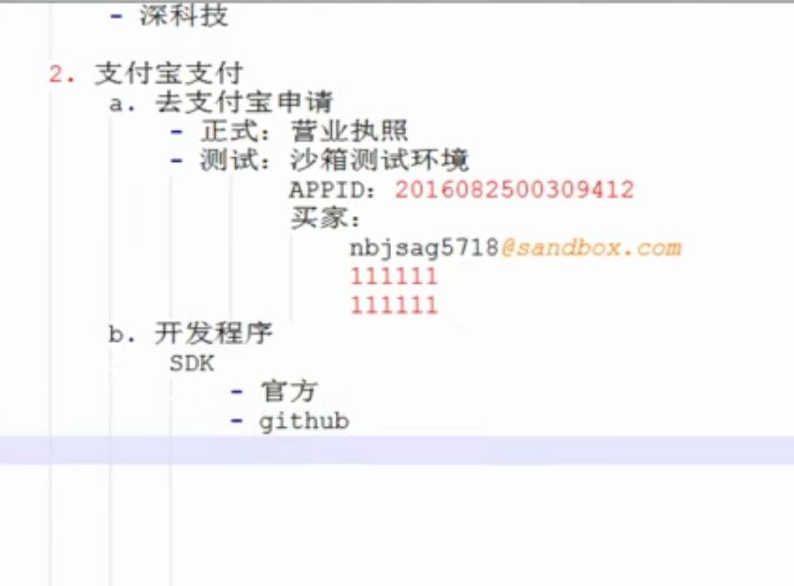
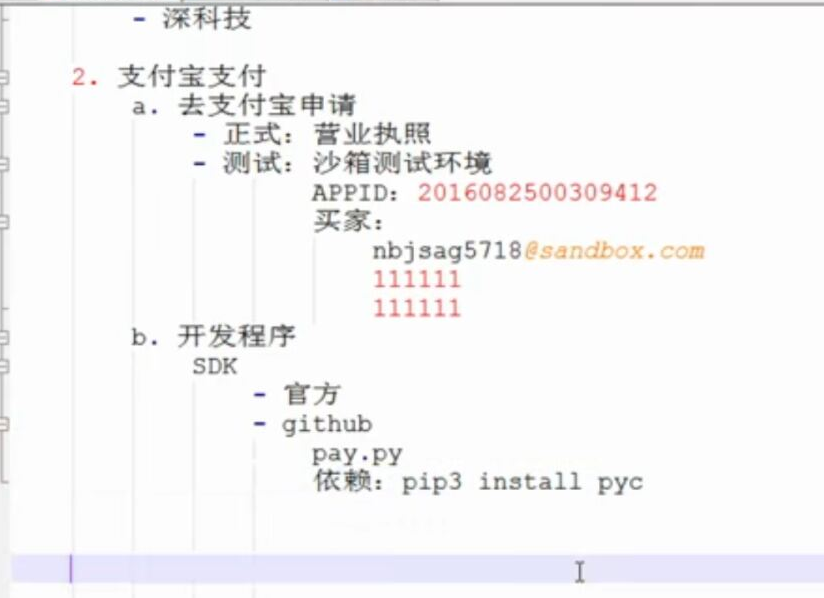
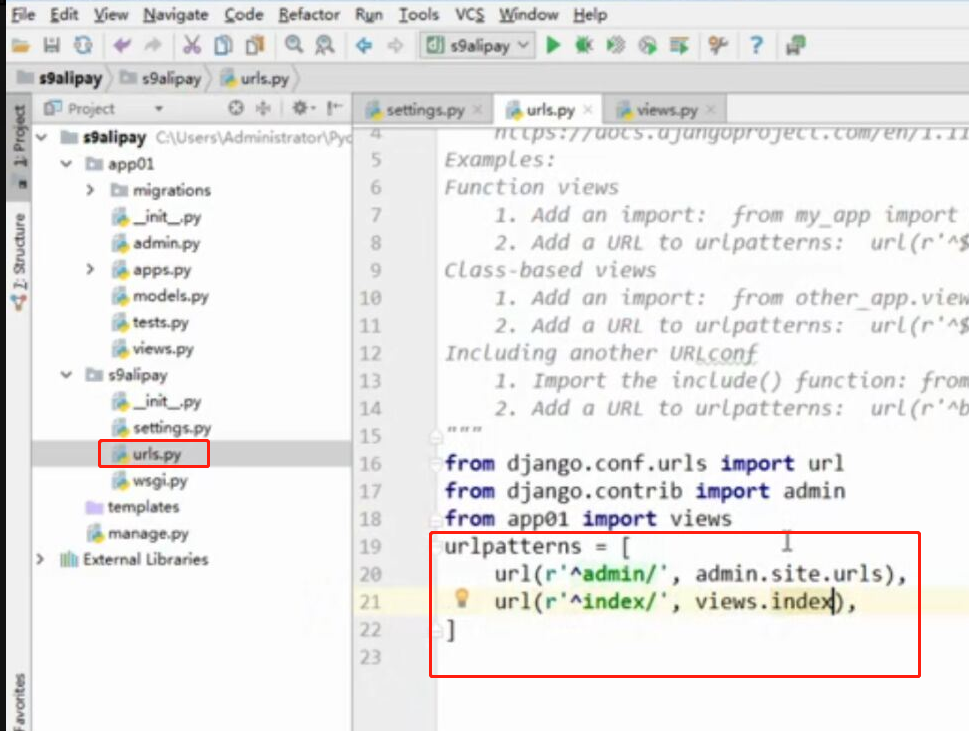
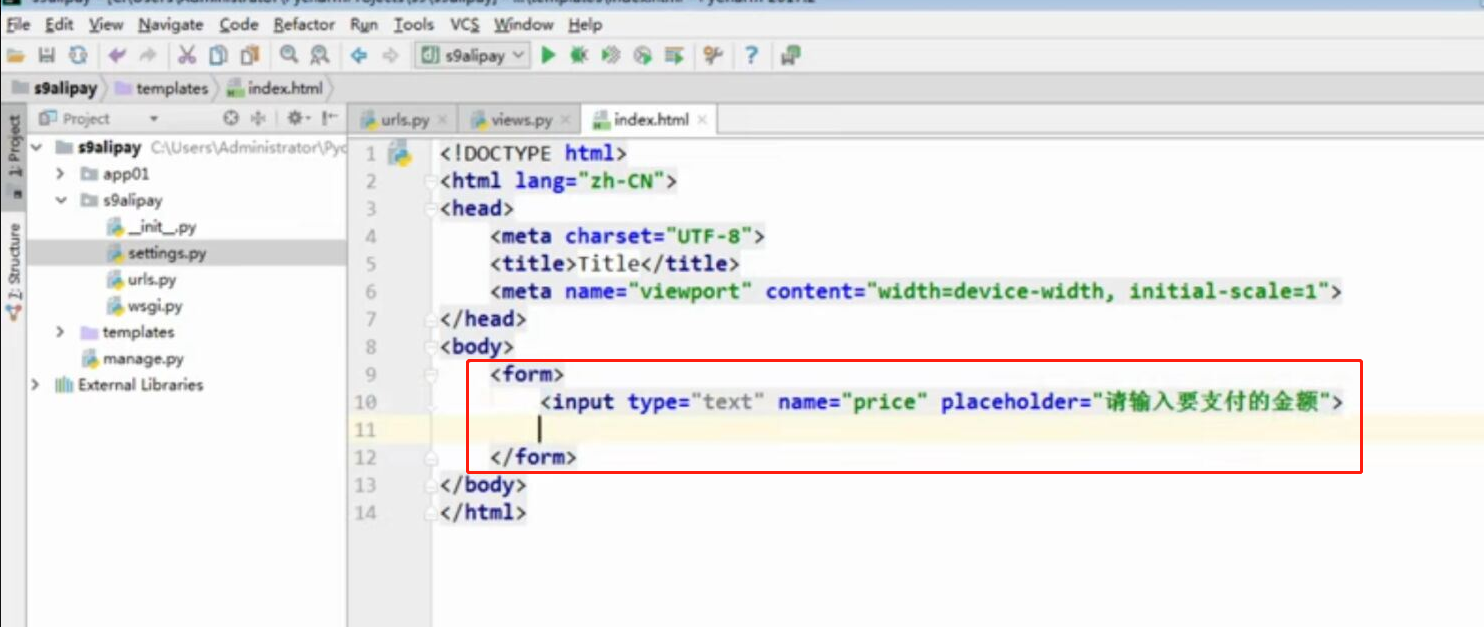
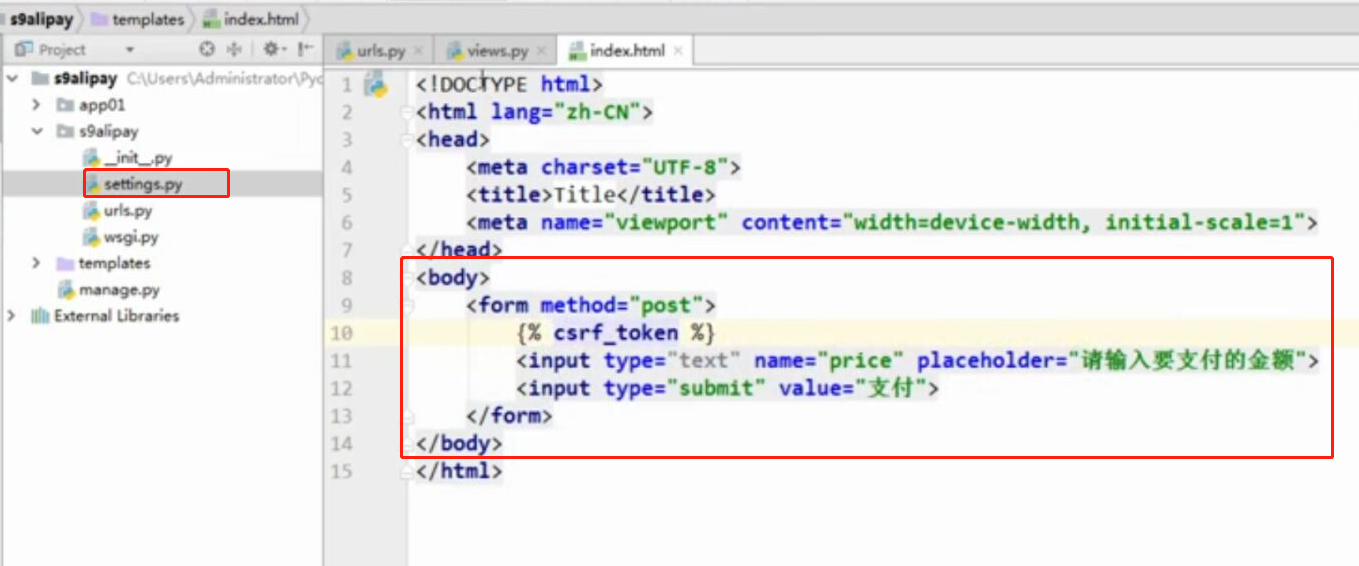
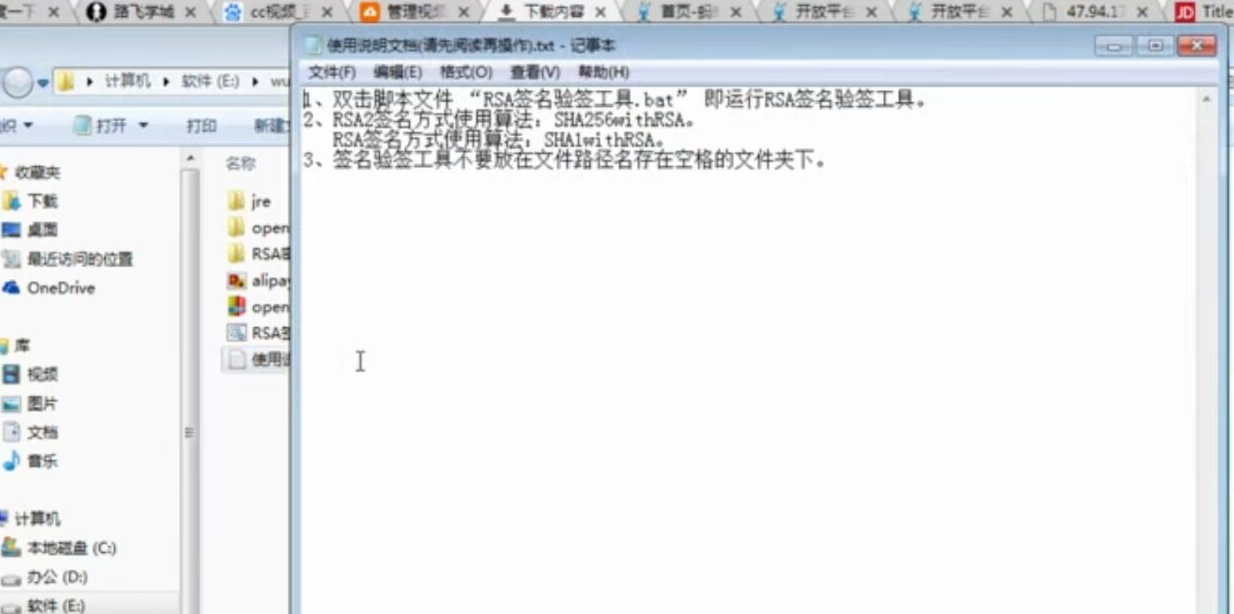
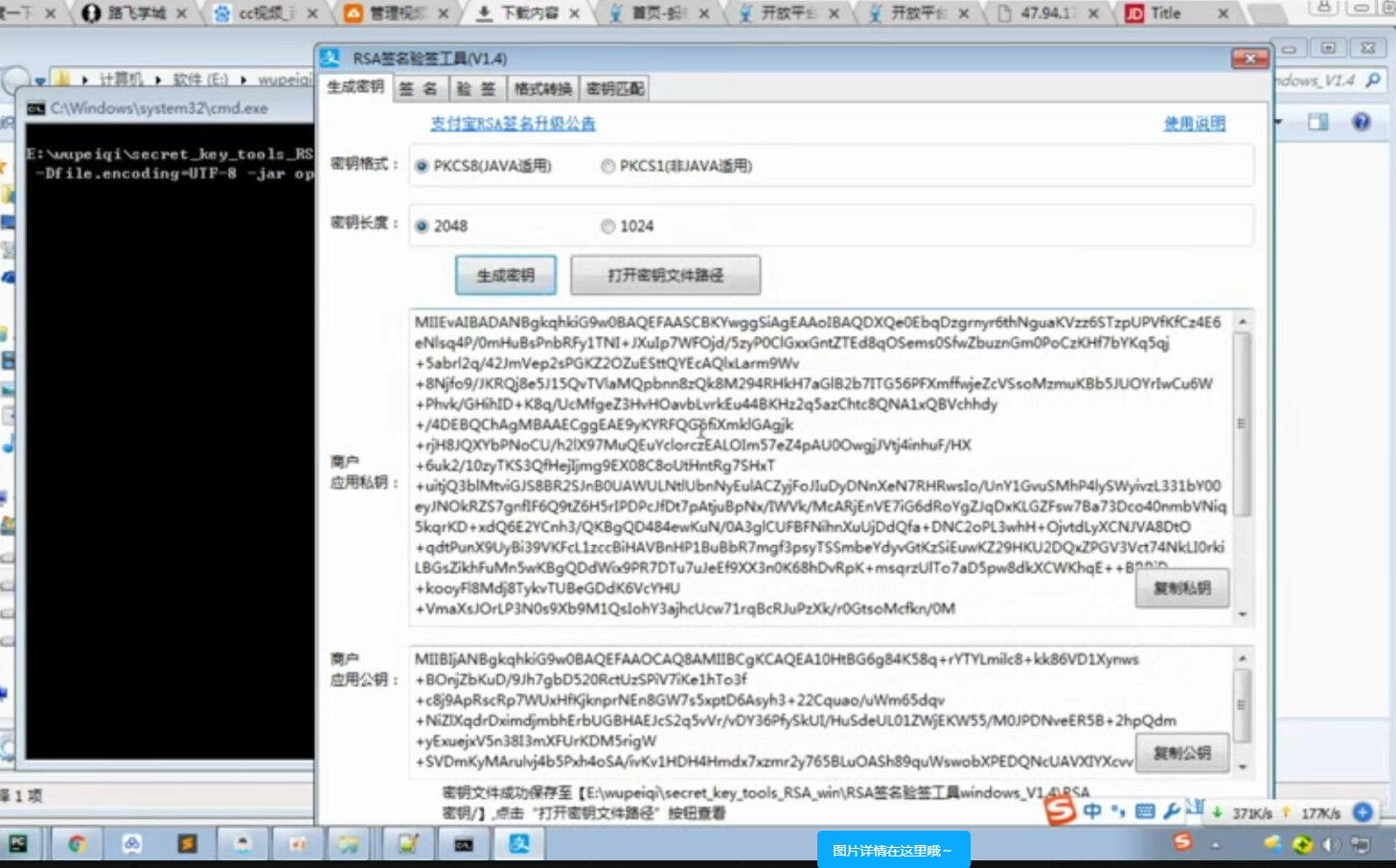
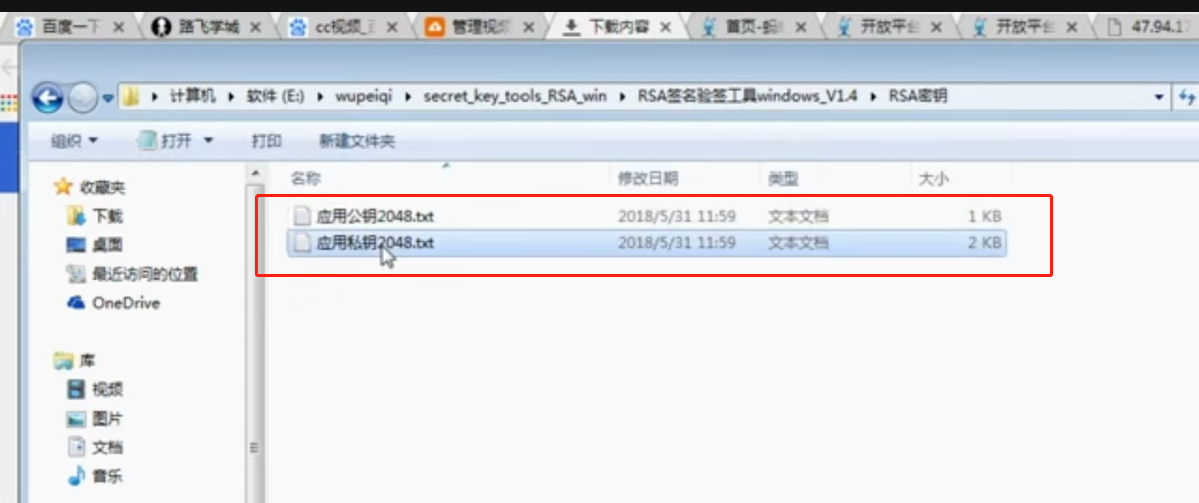
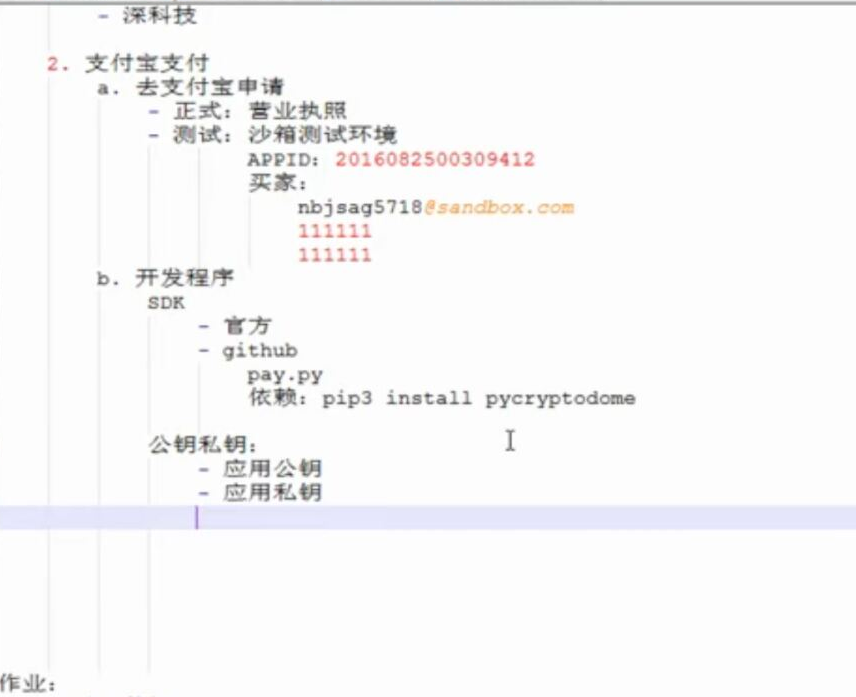
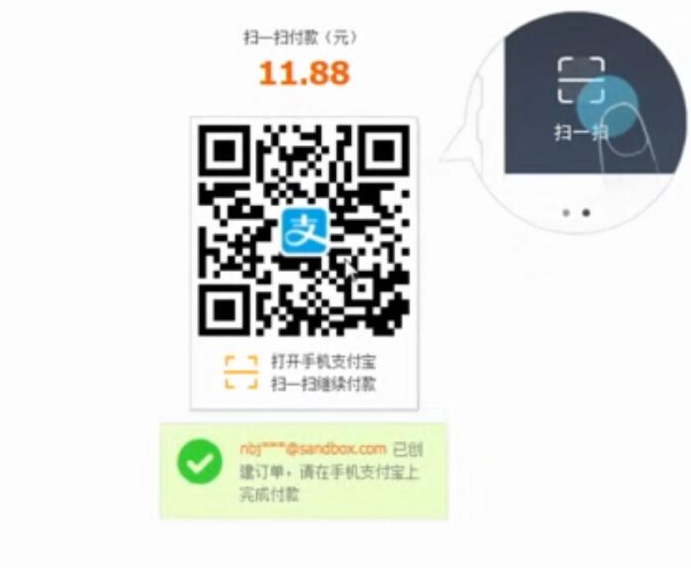
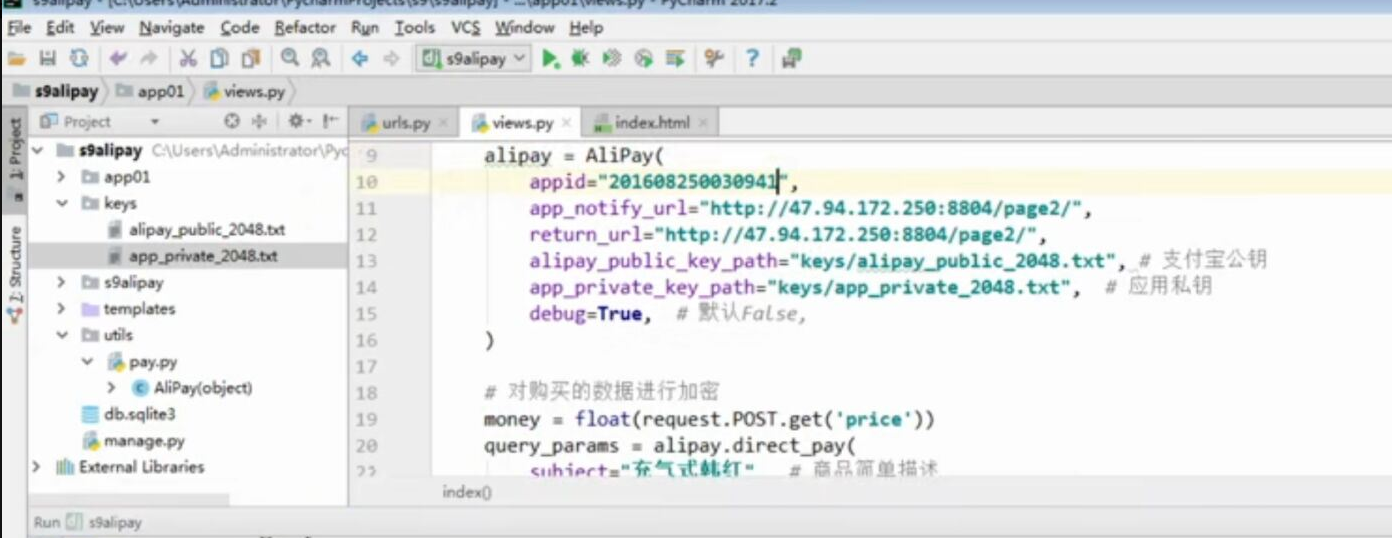
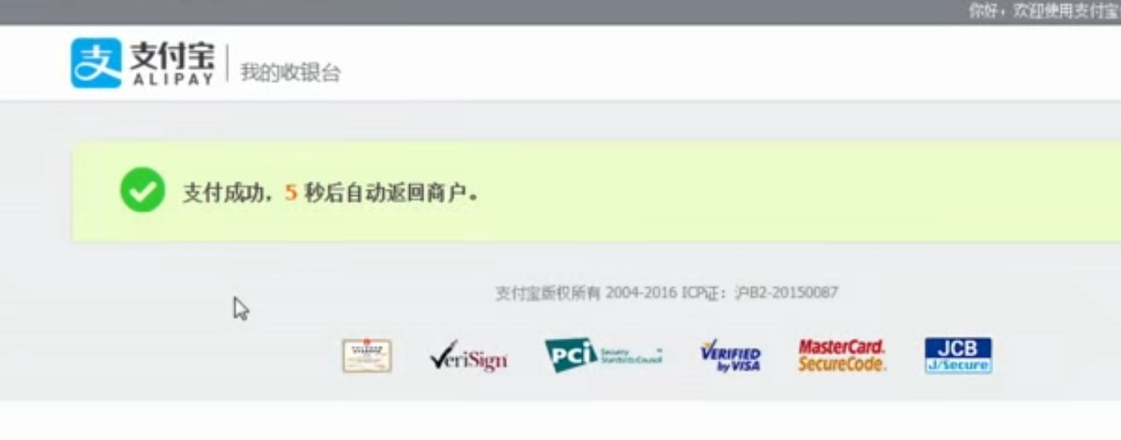
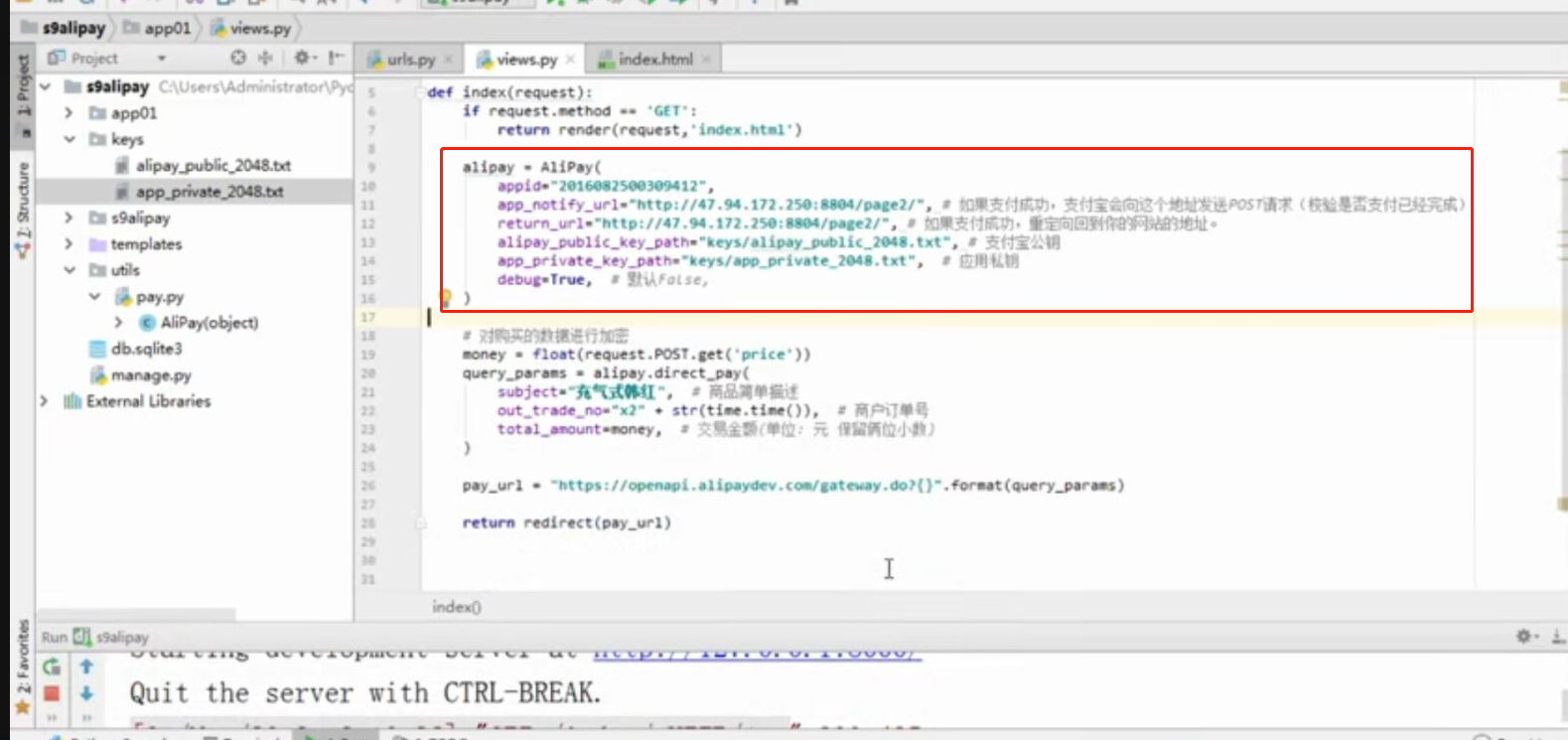
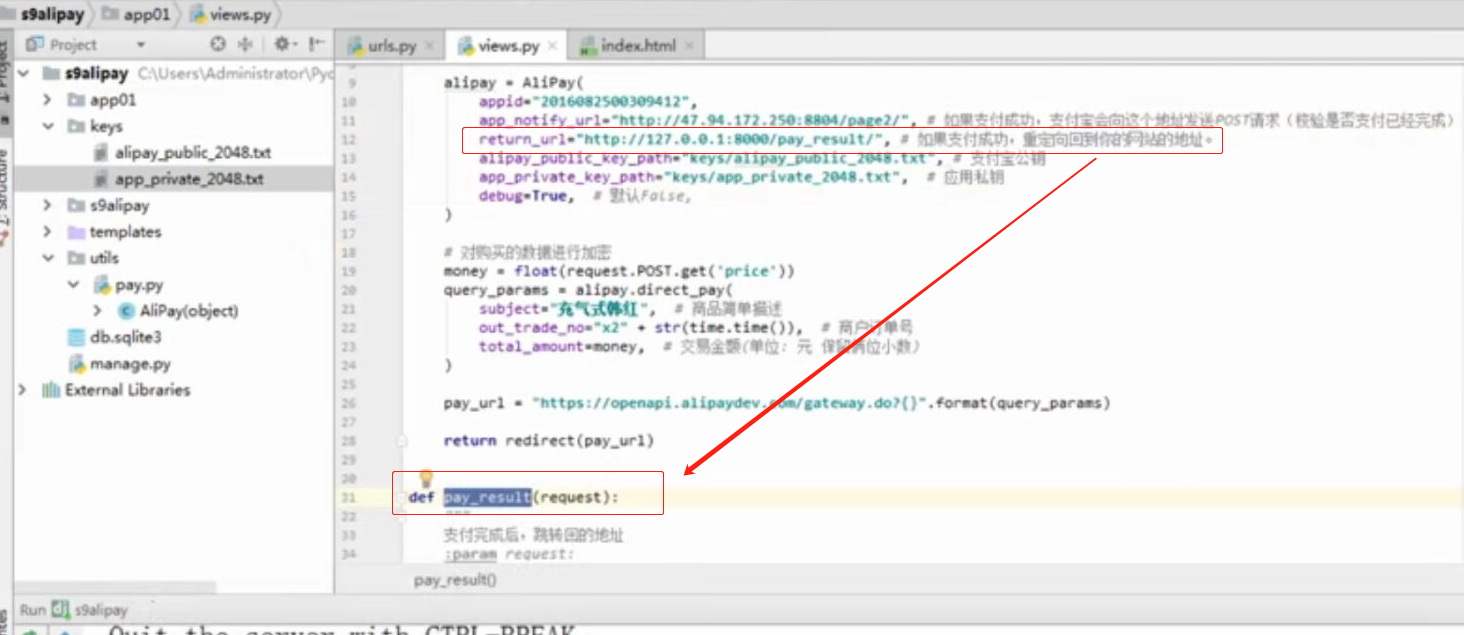
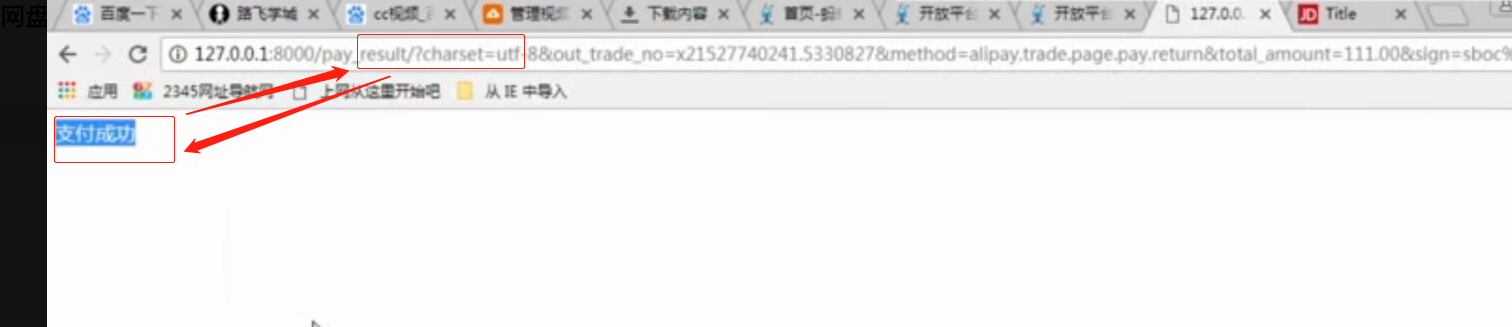
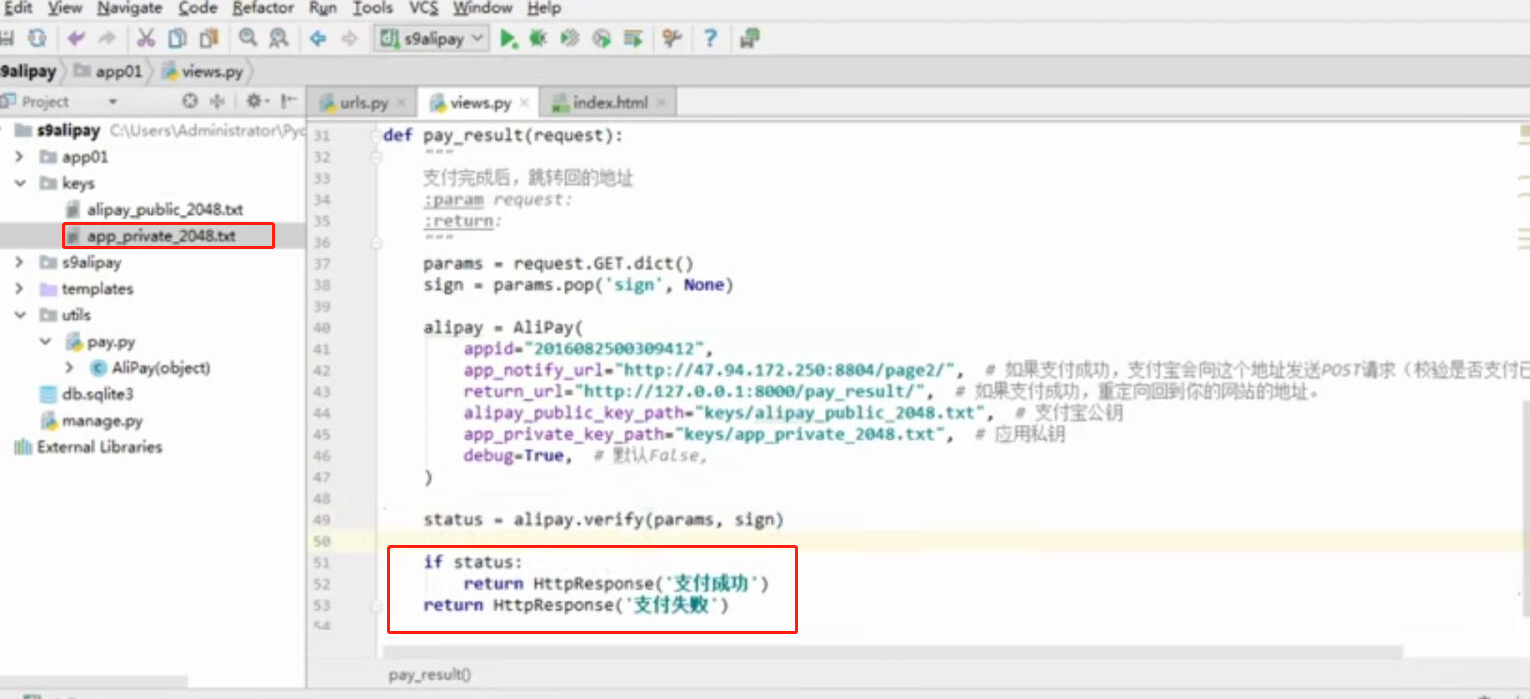
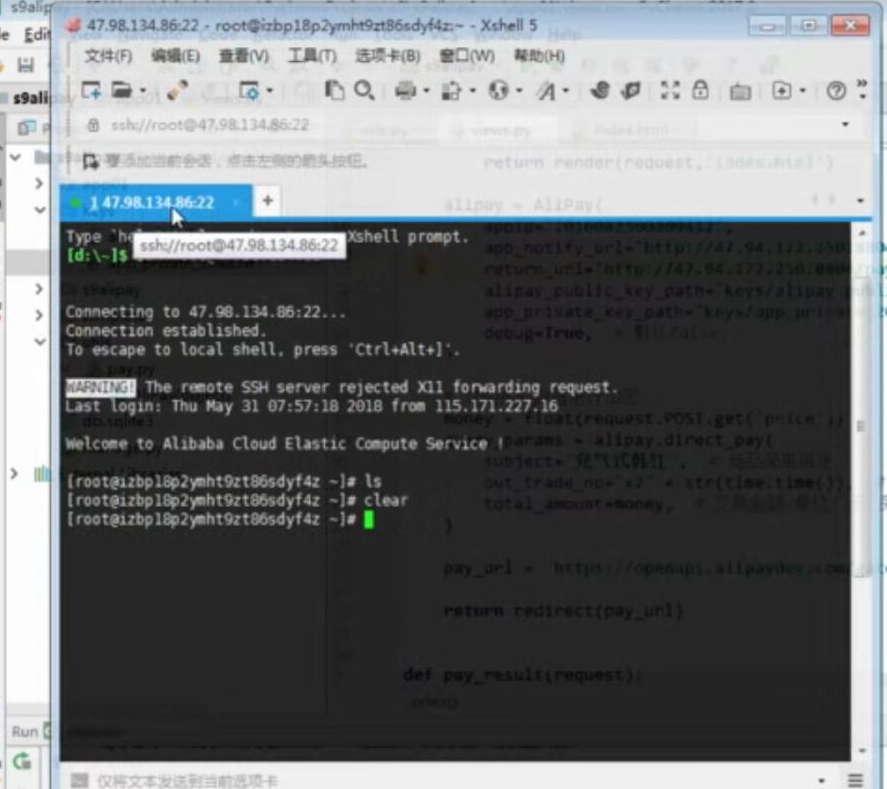
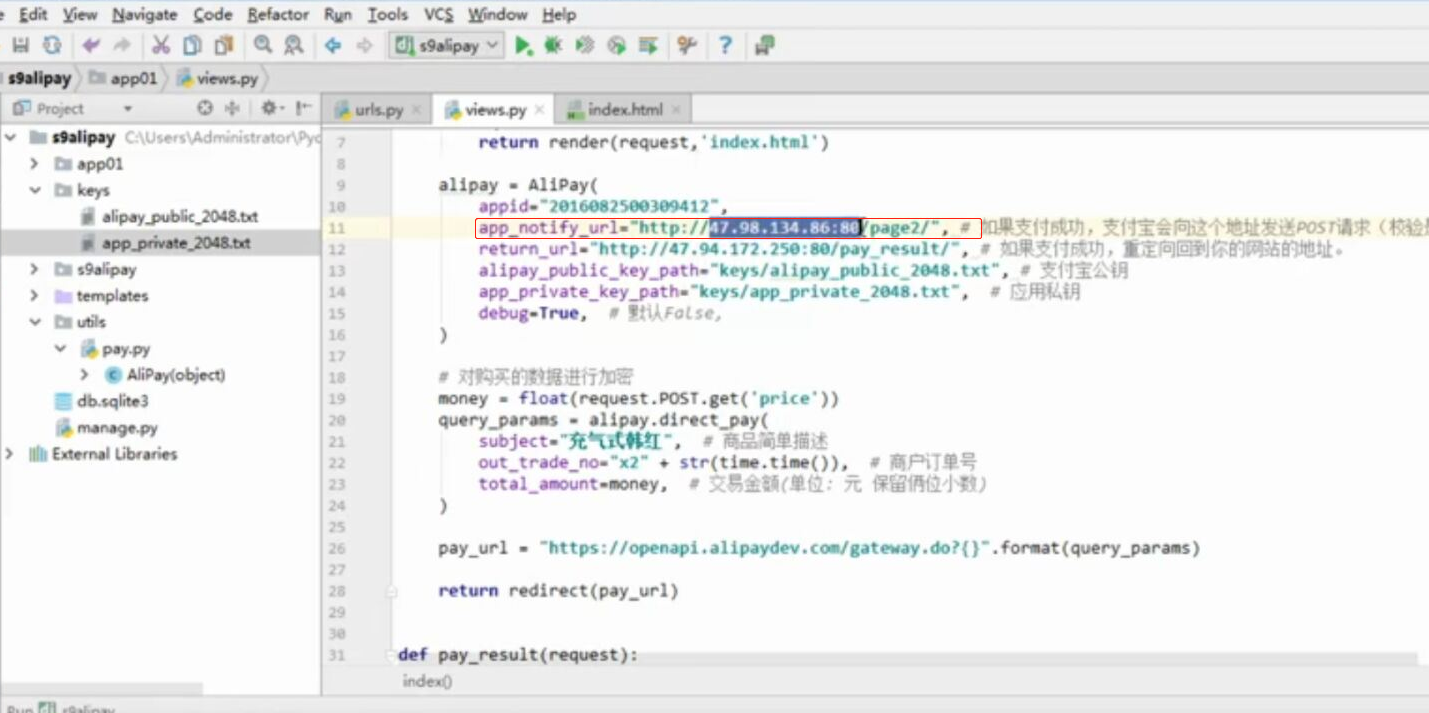
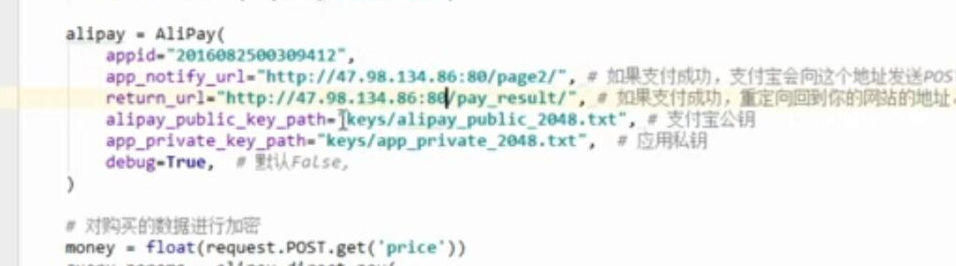
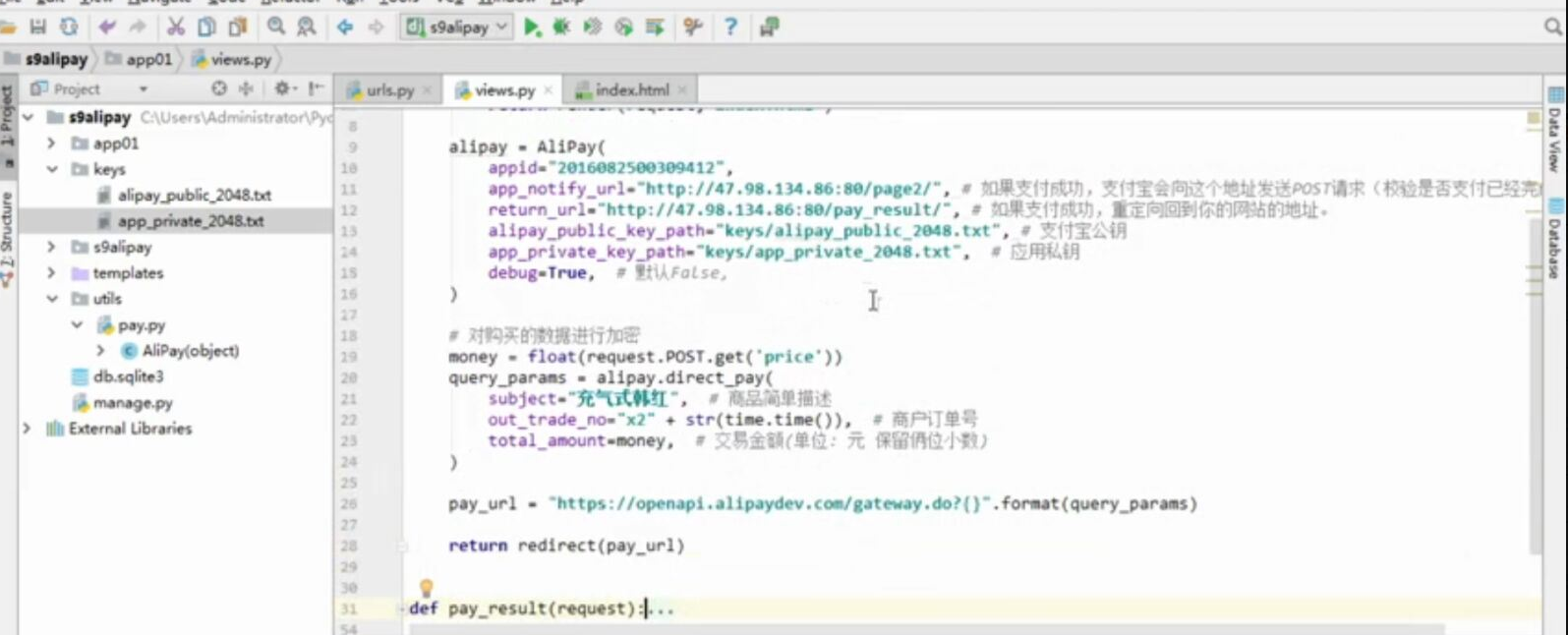
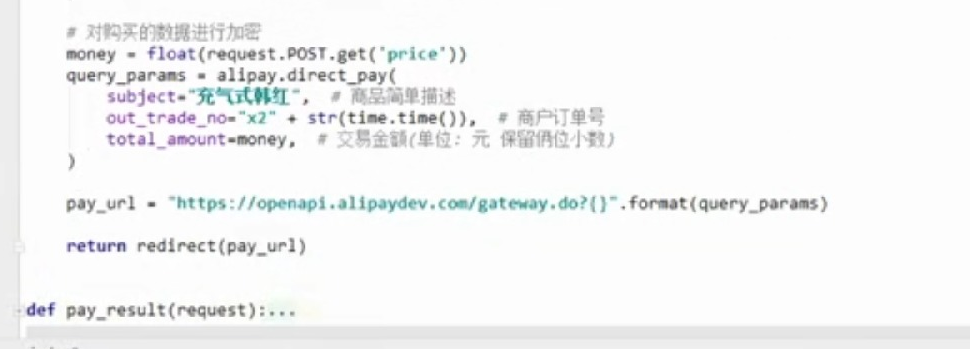
WEB知识补充 支付宝 支付的更多相关文章
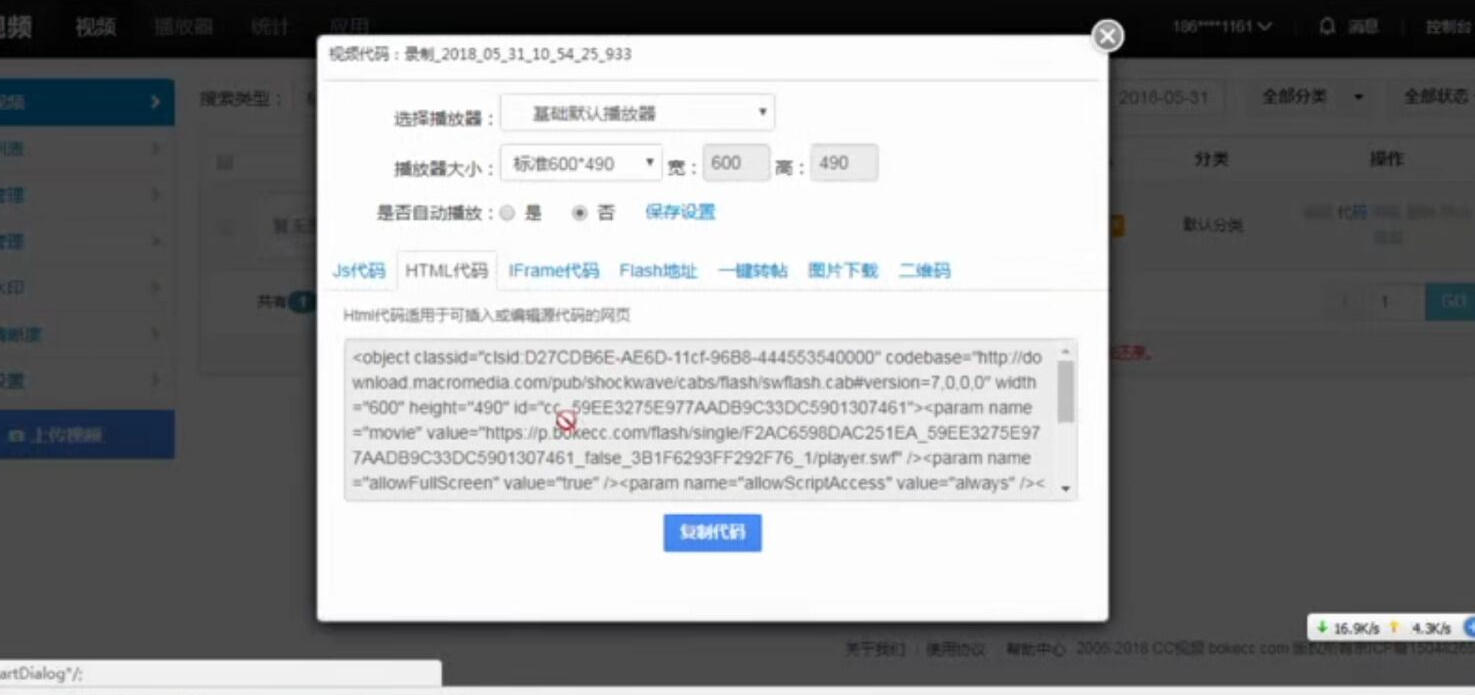
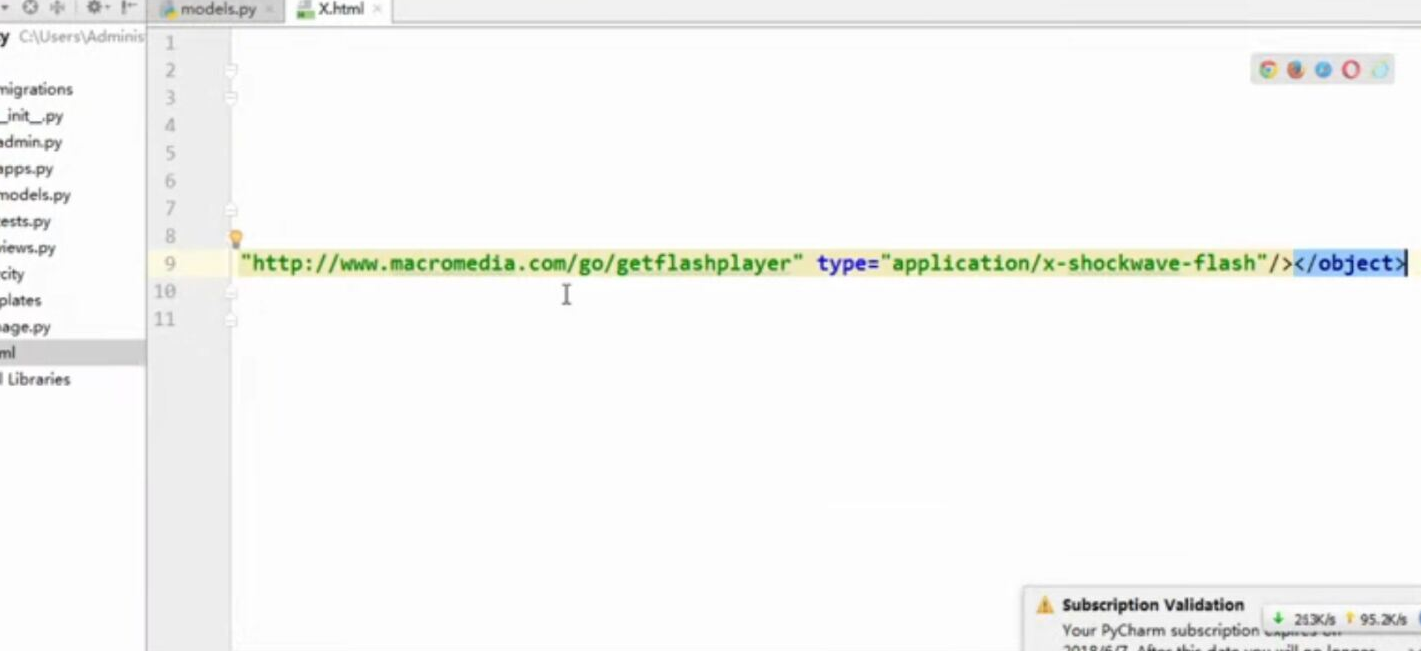
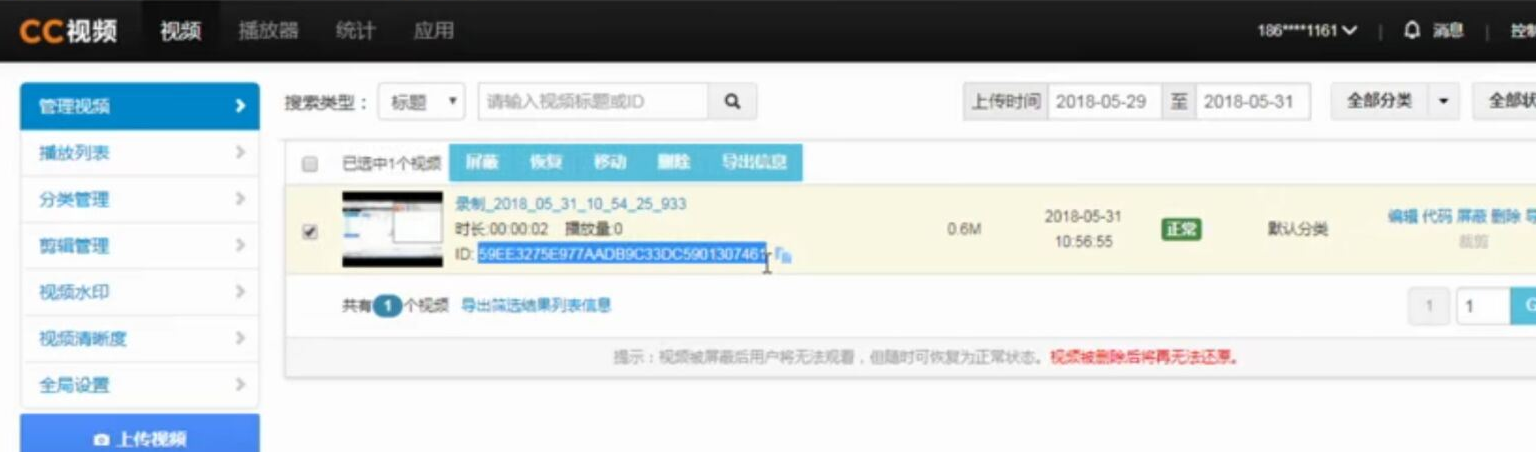
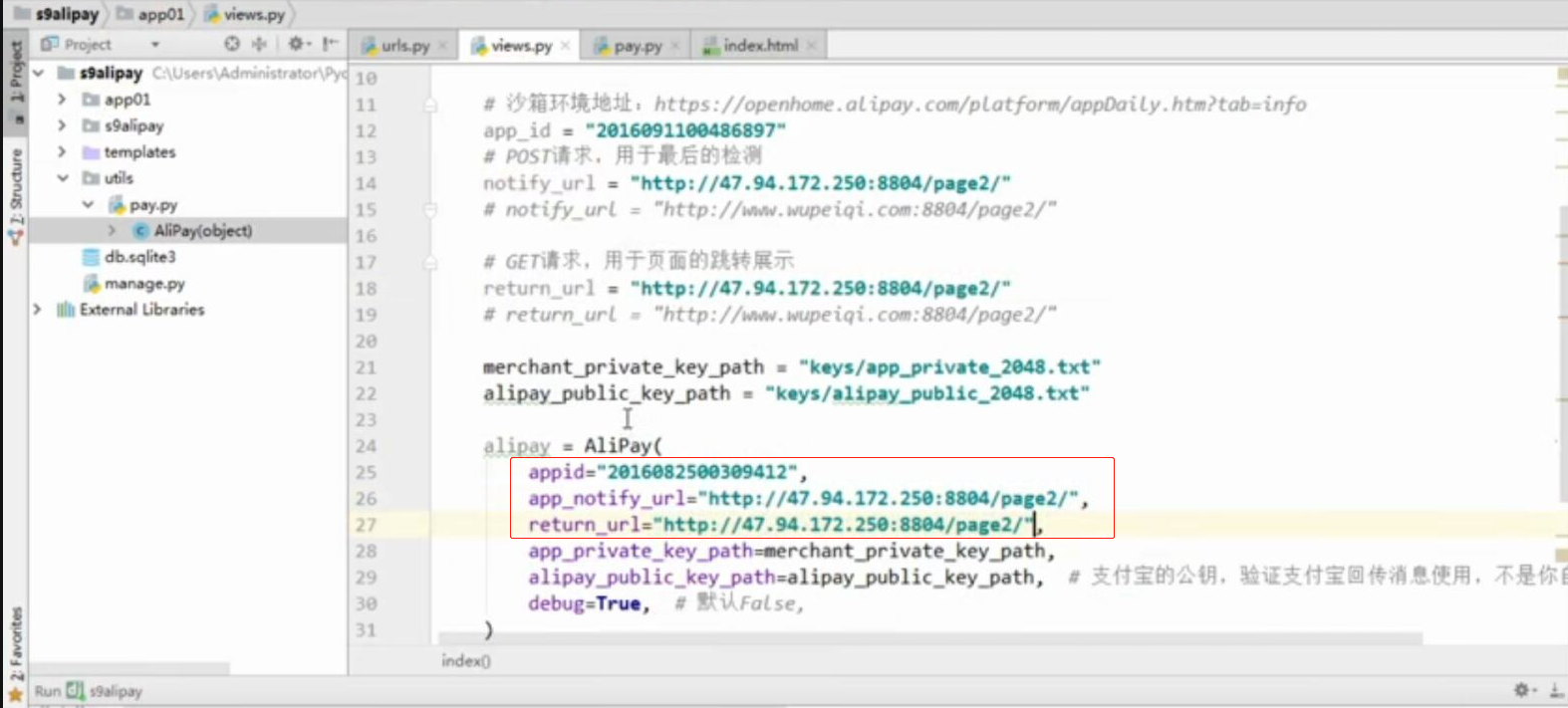
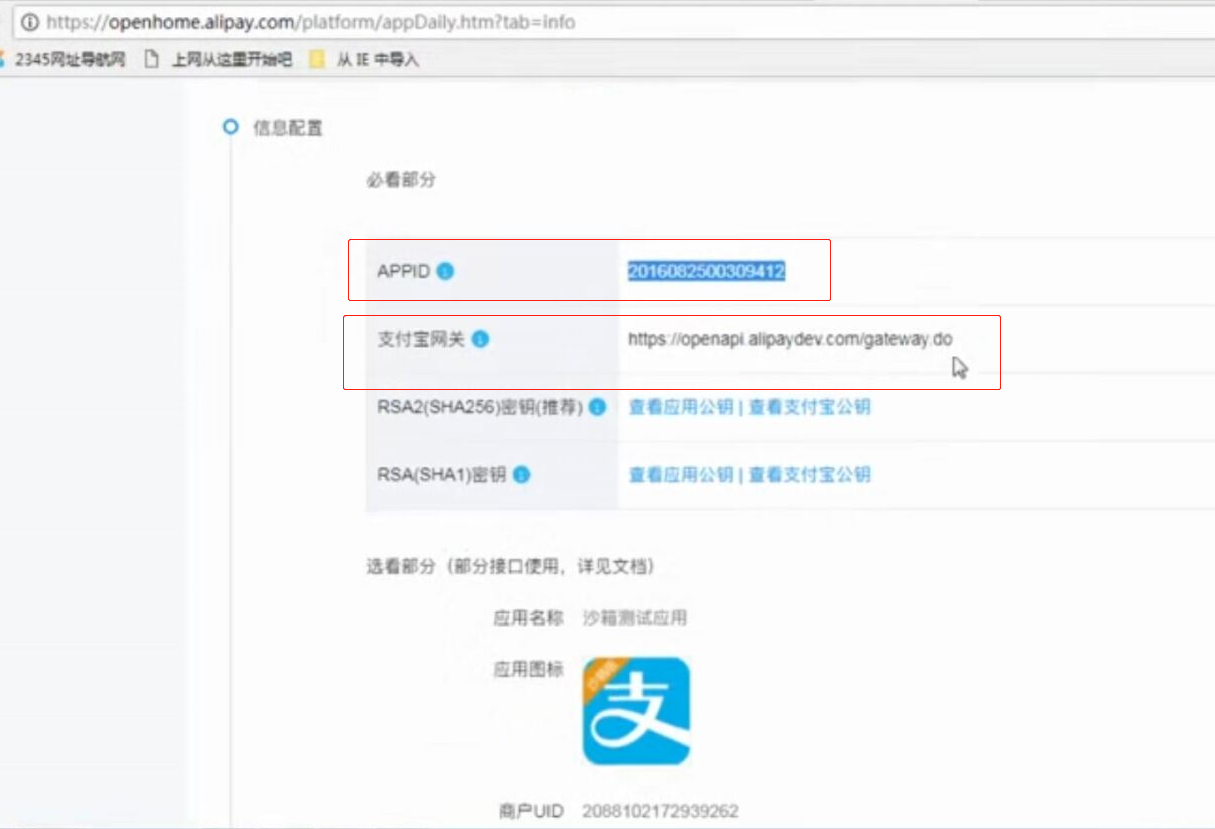
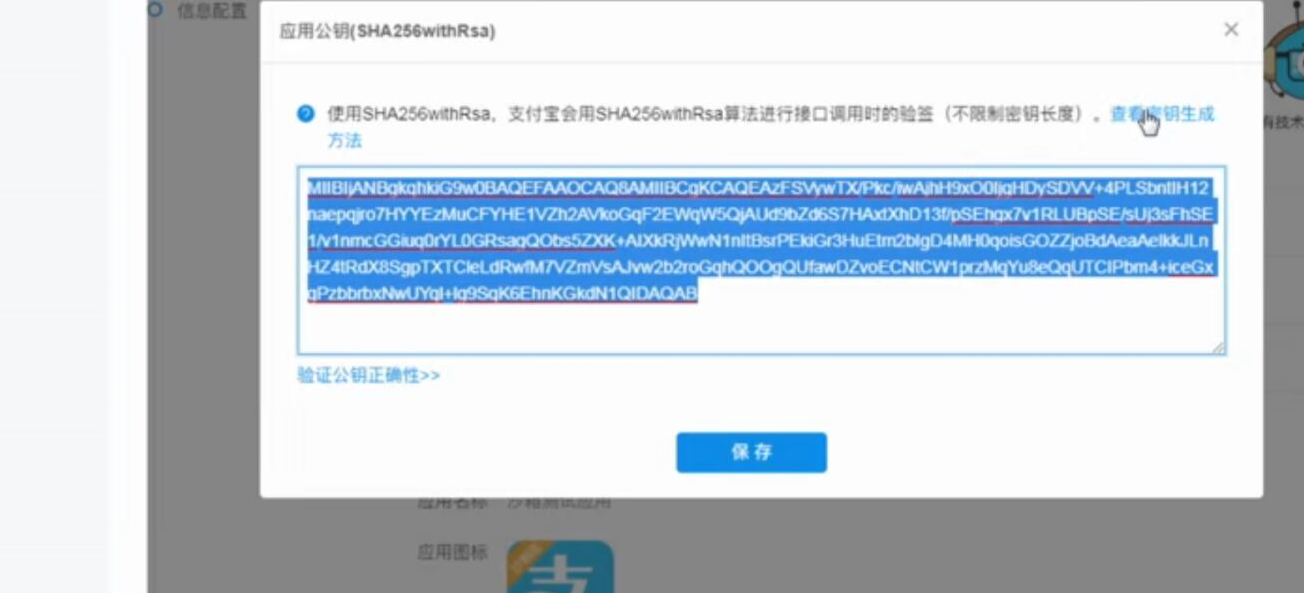
- web页面调用支付宝支付
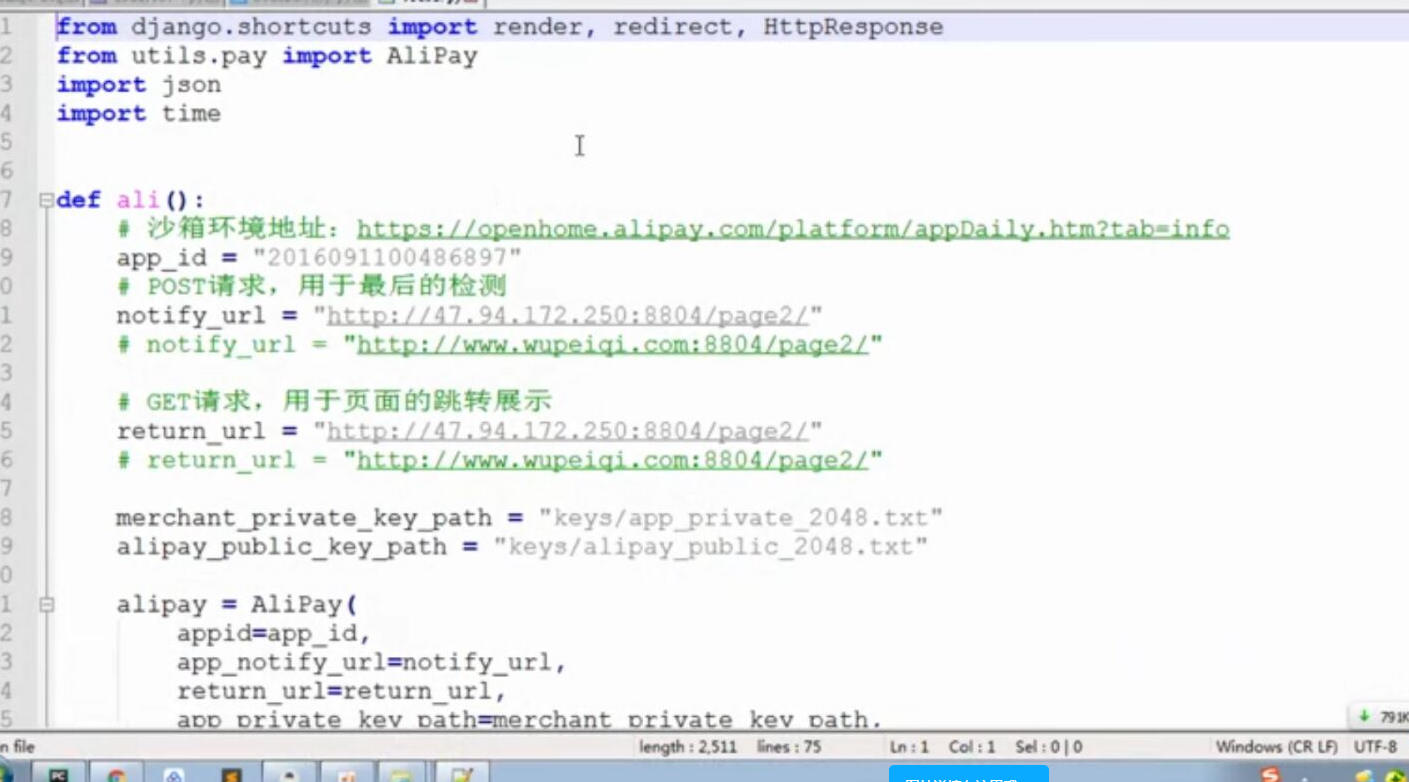
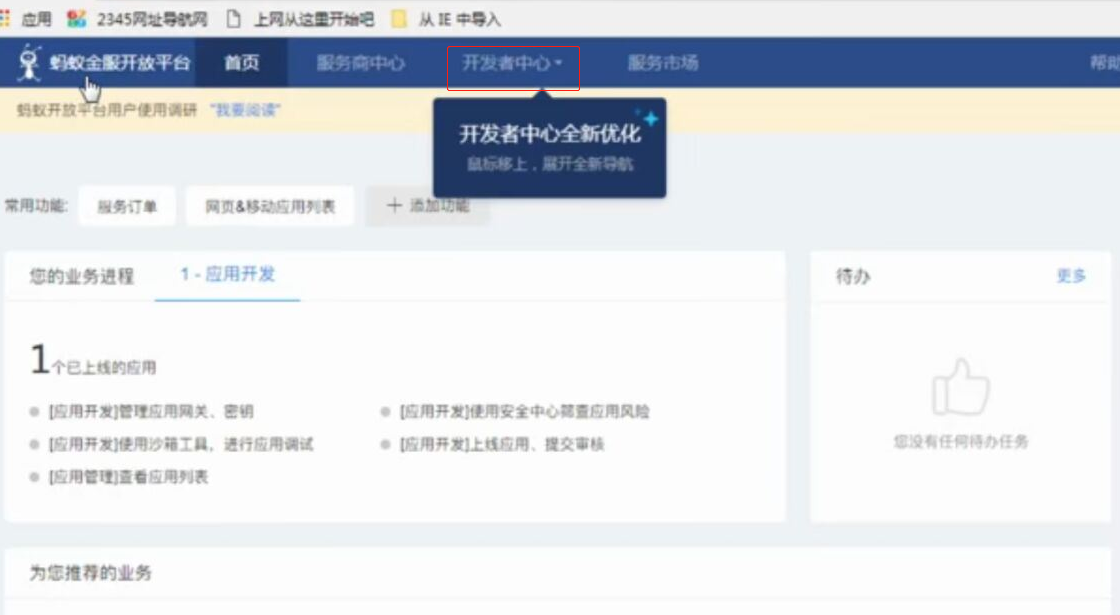
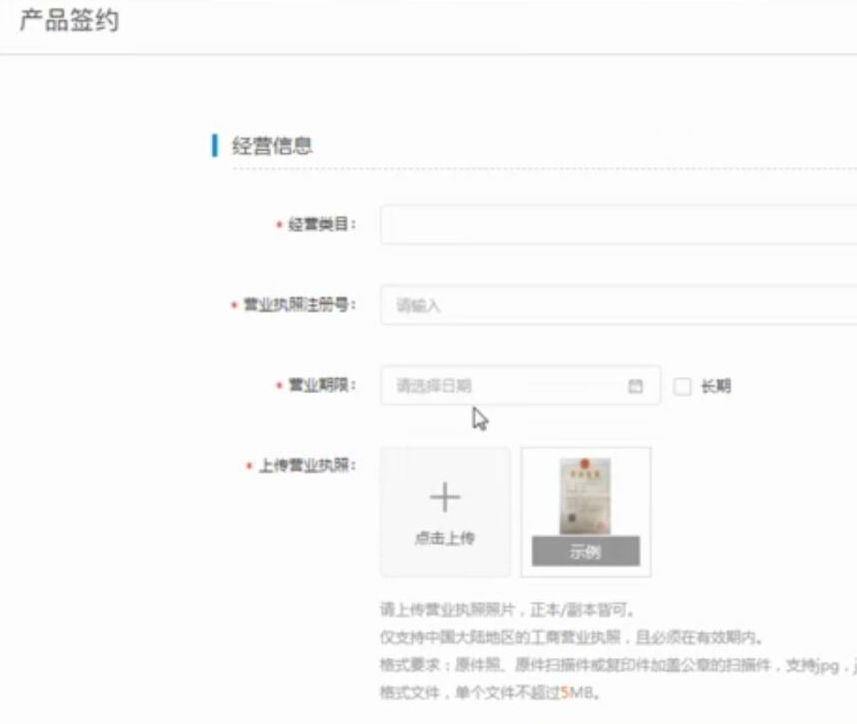
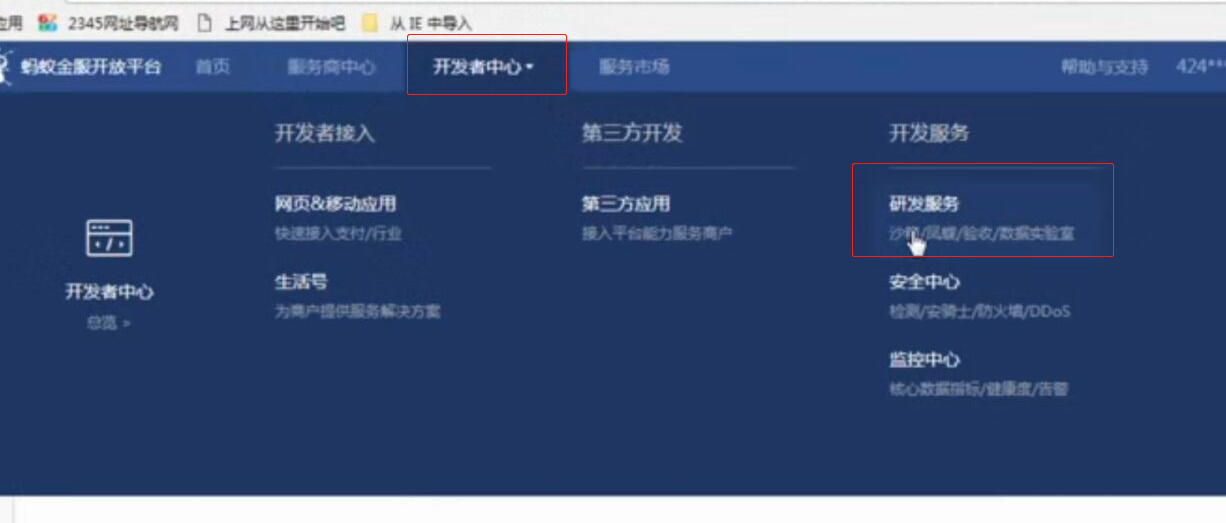
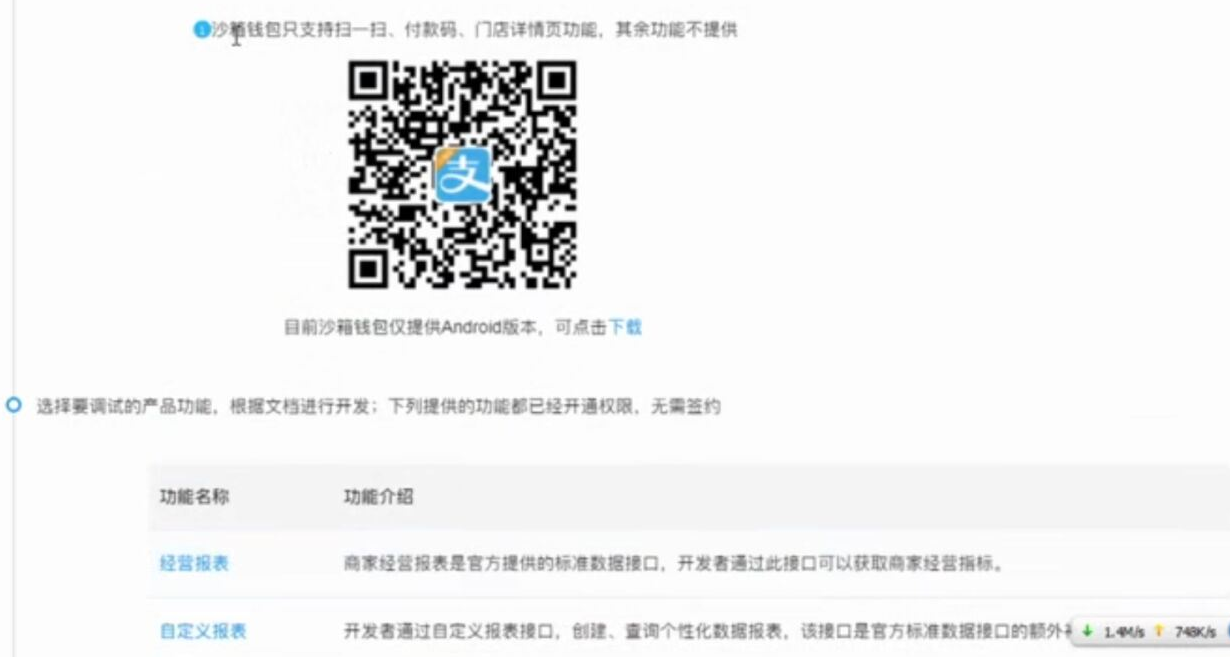
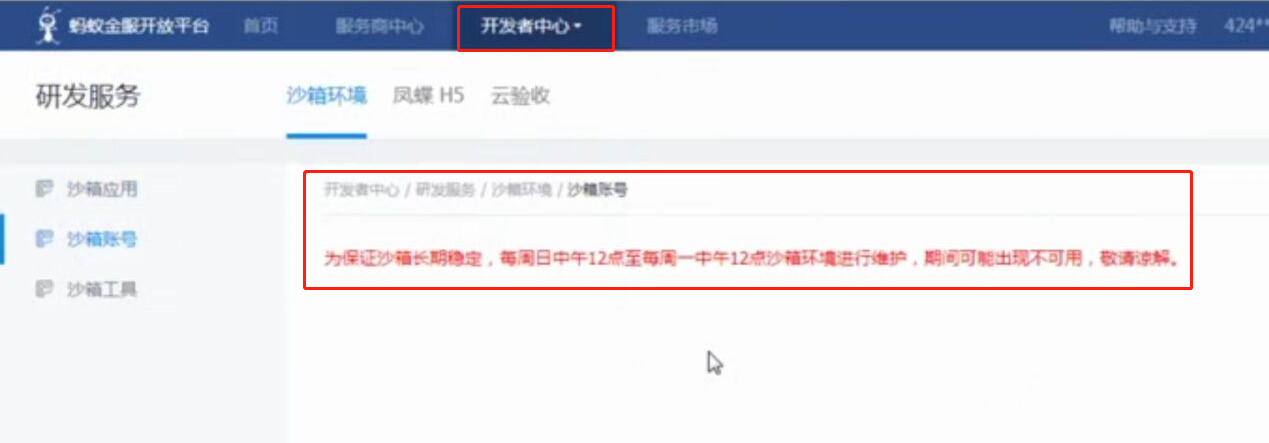
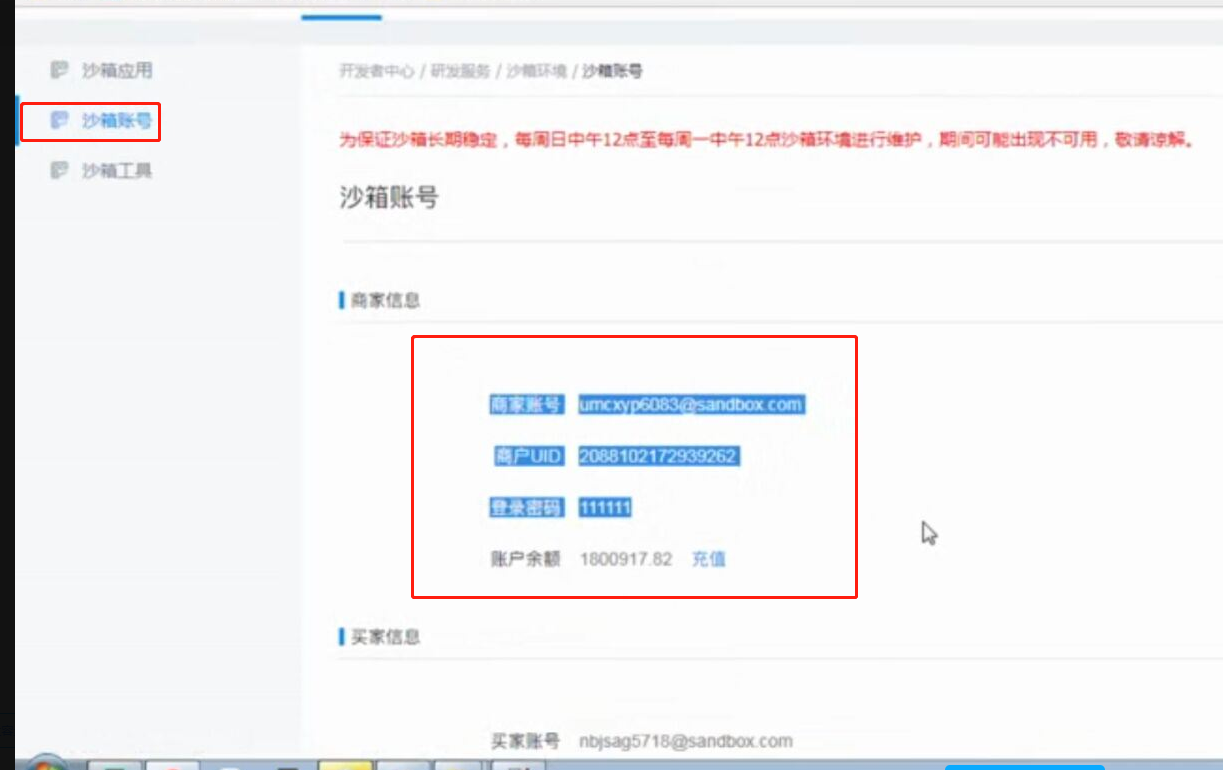
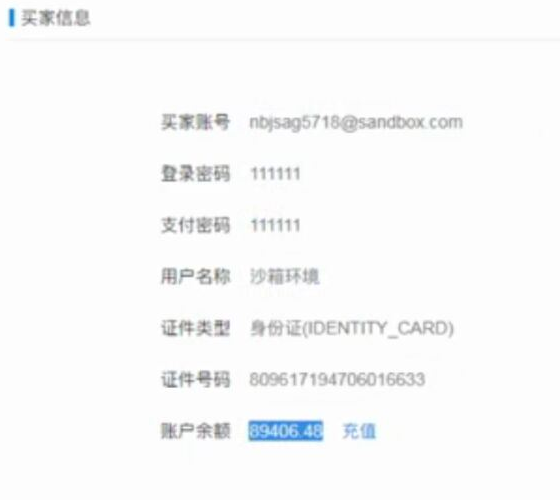
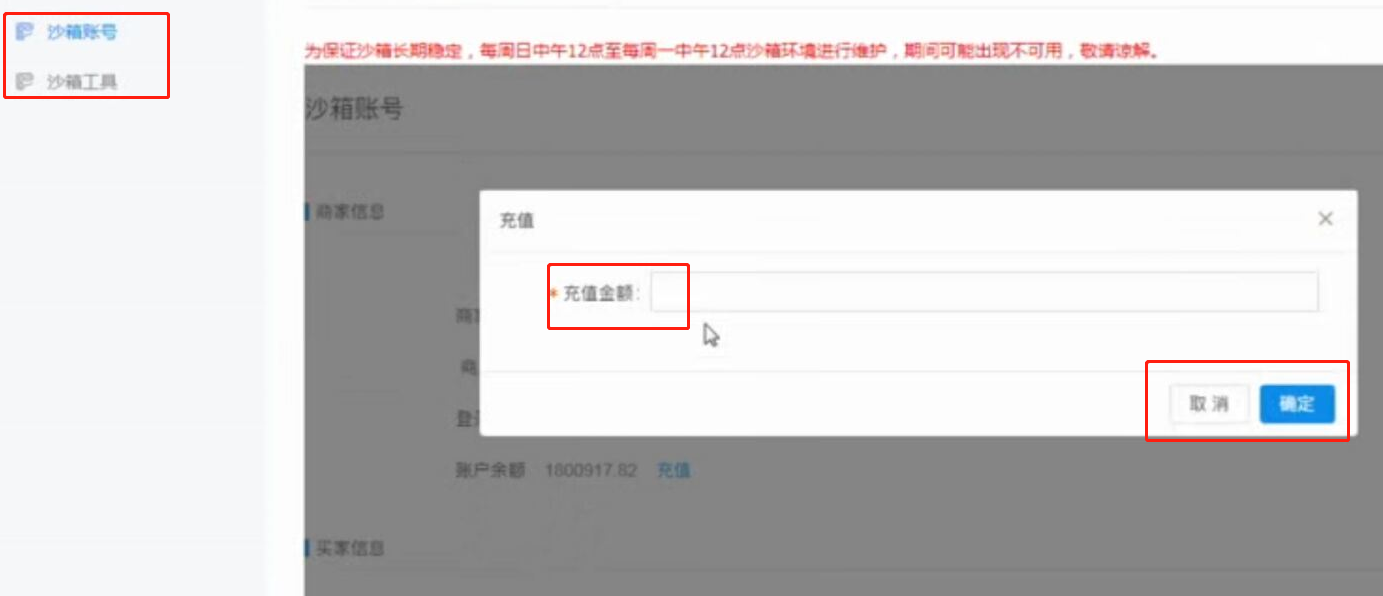
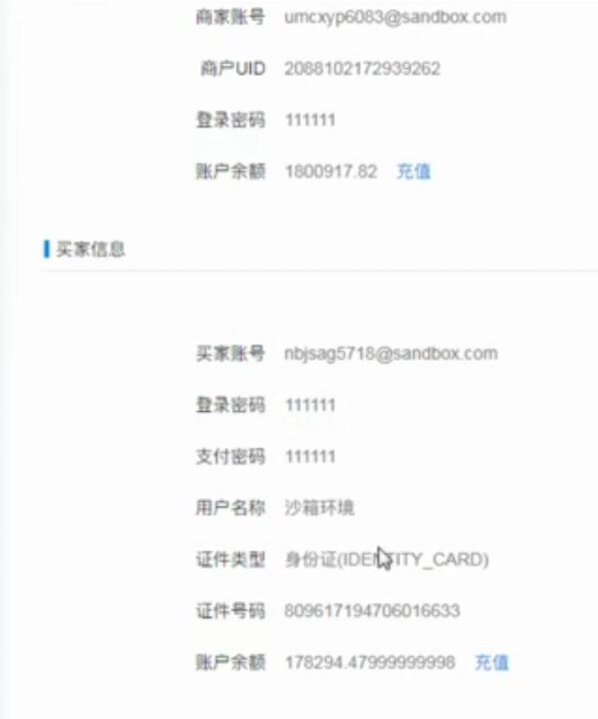
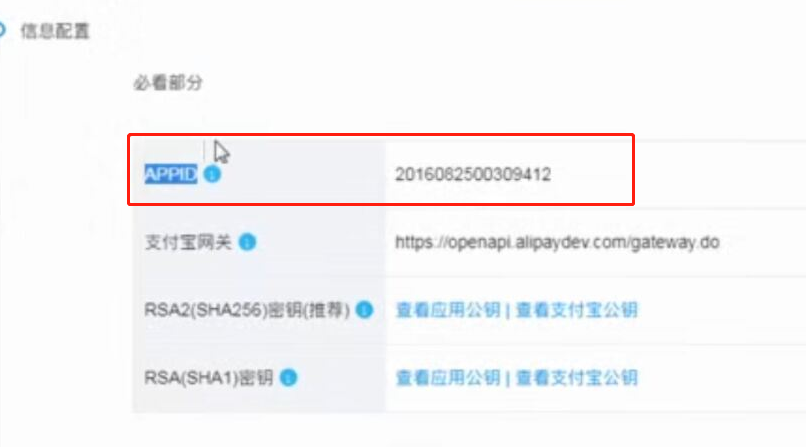
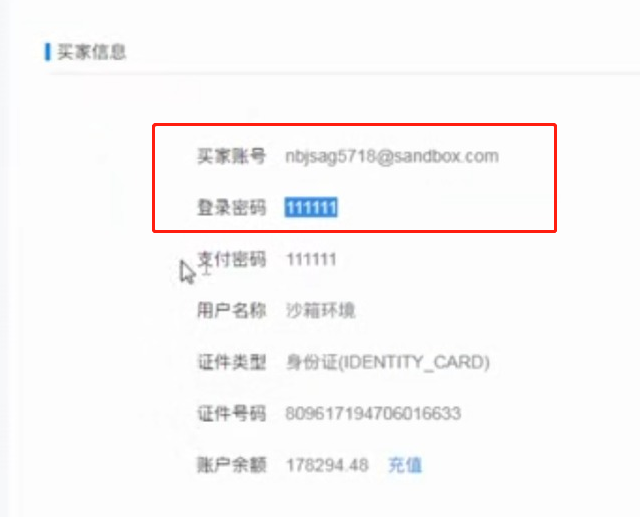
web页面调用支付宝支付 此文章是前端单独模拟完成支付,若在线上环境则需要后台配合产生签名等参数 在蚂蚁金服开放平台申请沙箱环境 将沙箱环境中的密钥.应用网关.回调地址补全,生成密钥的方法在此 配置好 ...
- 开始逐步补充下相关Web知识,很多年没搞了....
<script type="text/javascript"> $(function(){ ShowProduct(); $("#ShowUserInfo&q ...
- 【zhifu】web开发中的支付宝支付和微信支付
一.支付类型: 支付宝支付: 支付宝app内的网页支付: app外(即普通浏览器)网页支付: 微信支付: 微信app内的支付(在这里叫公众号支付) app外的支付(微信H5支付): 微信公众号的支付宝 ...
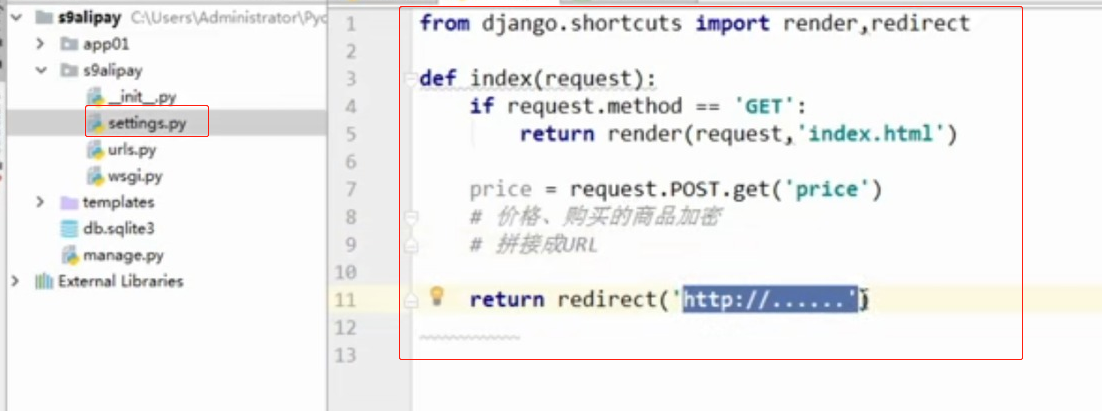
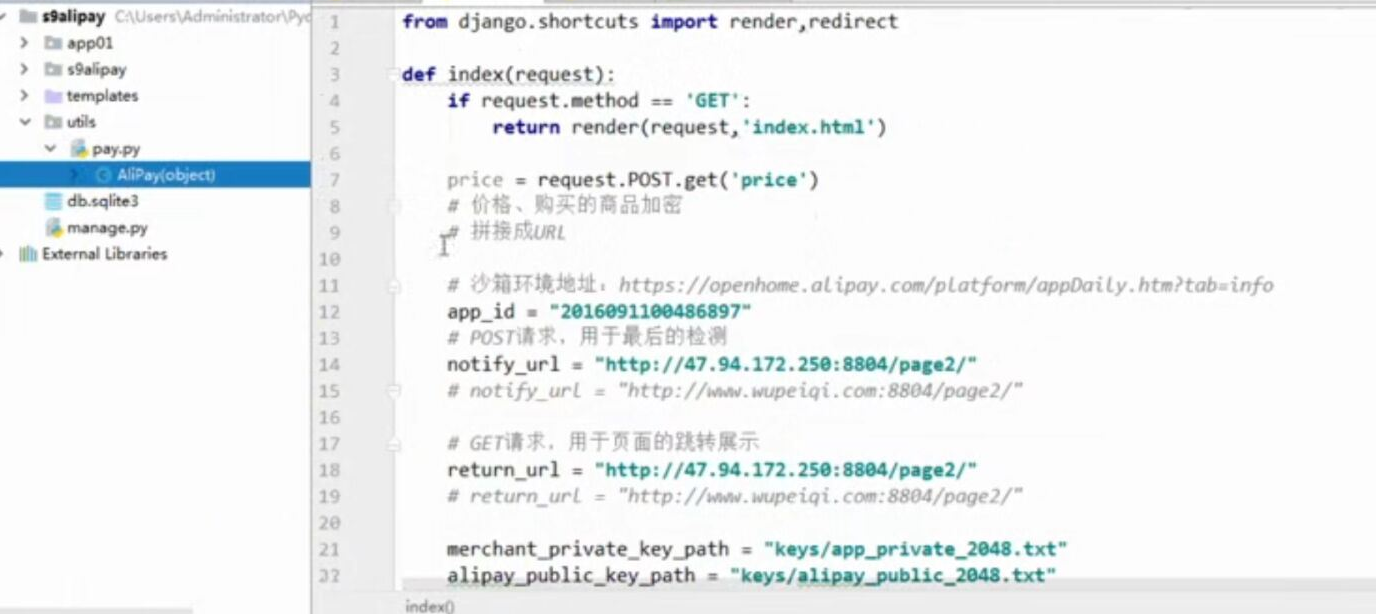
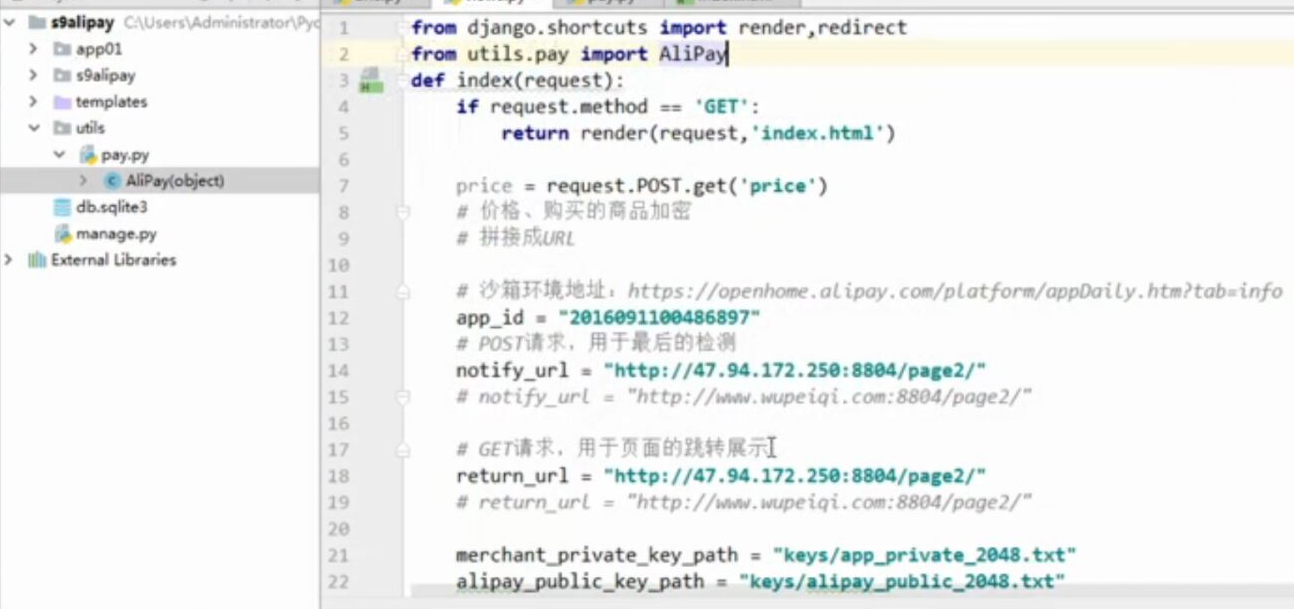
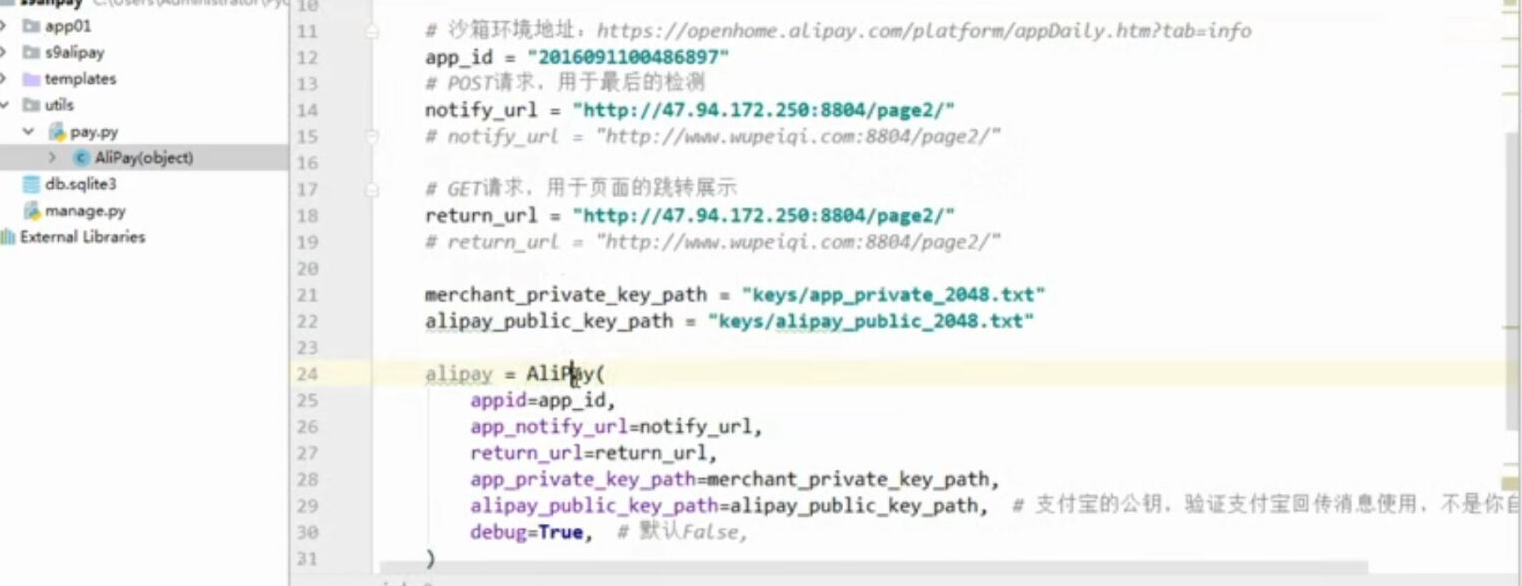
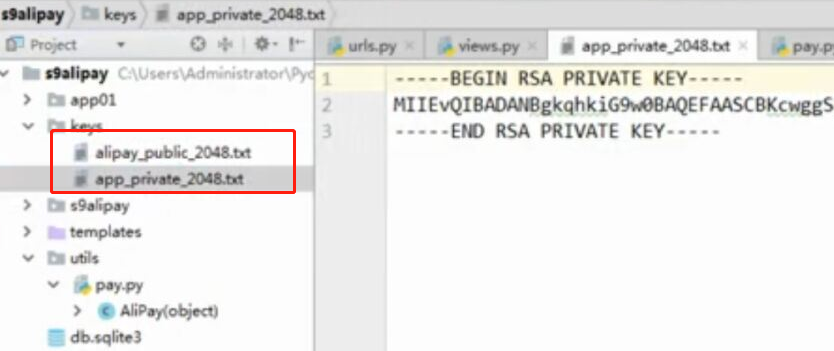
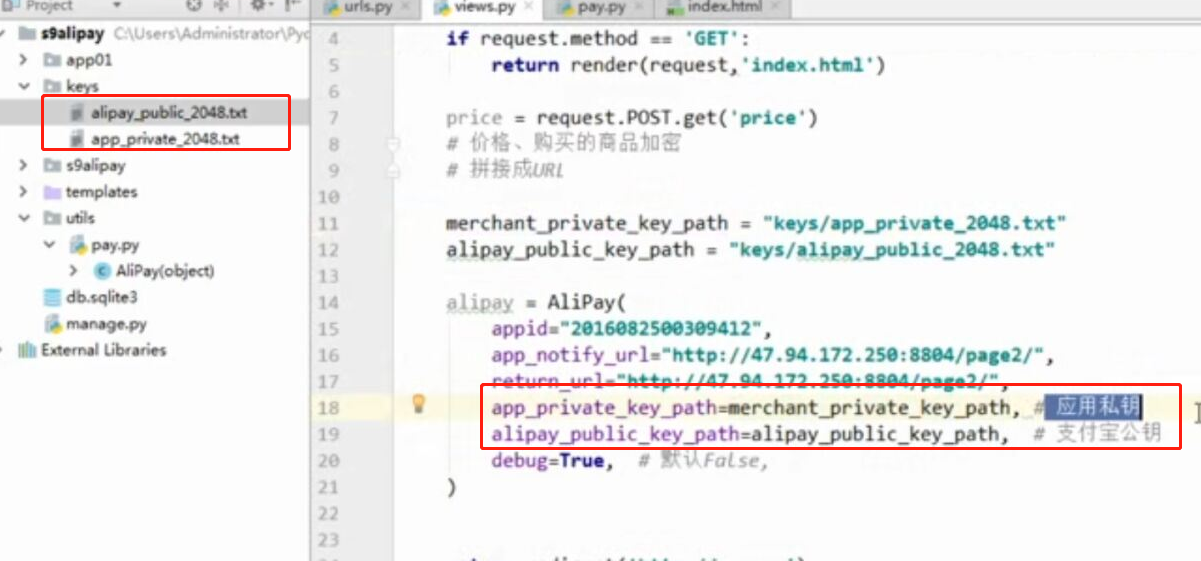
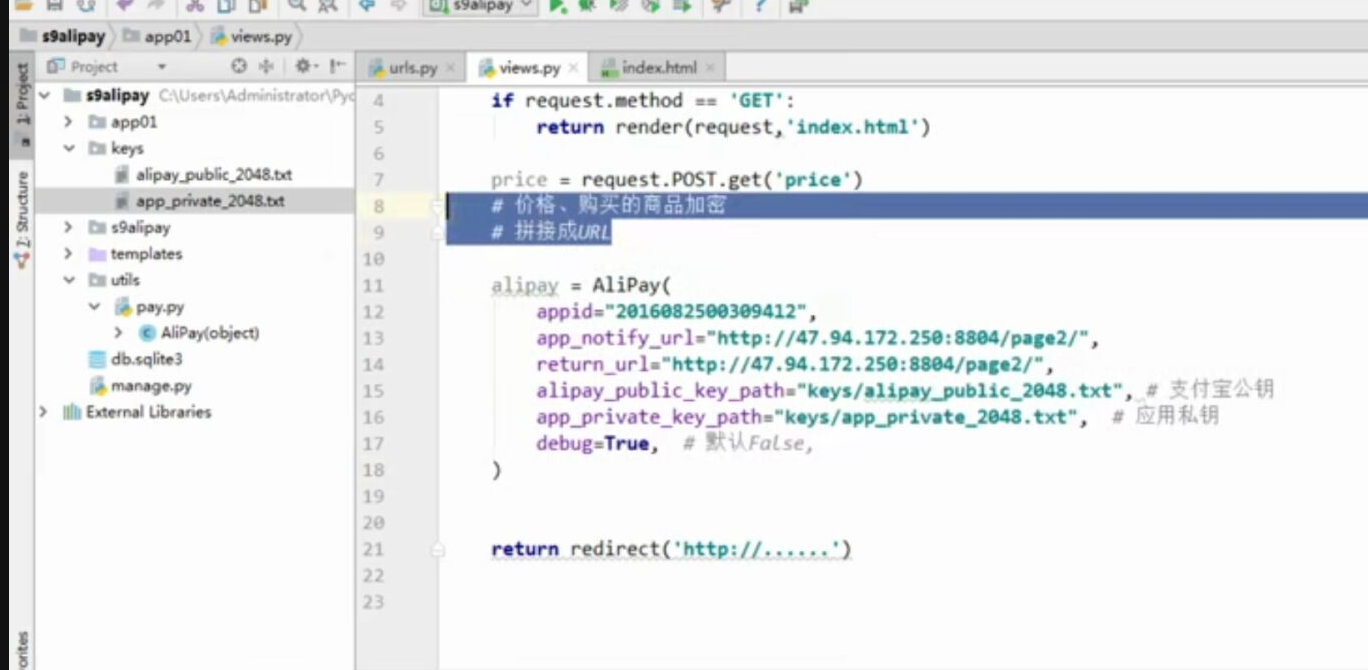
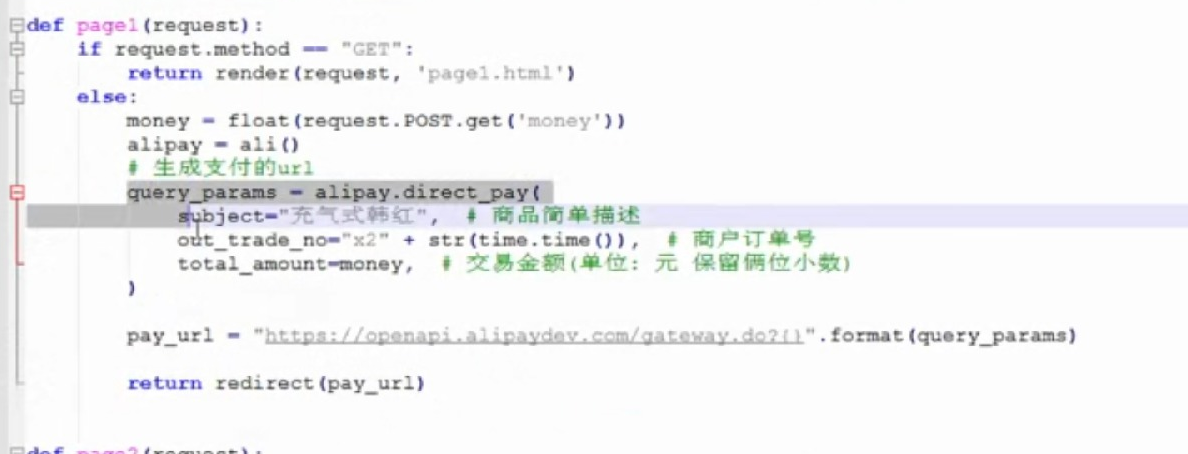
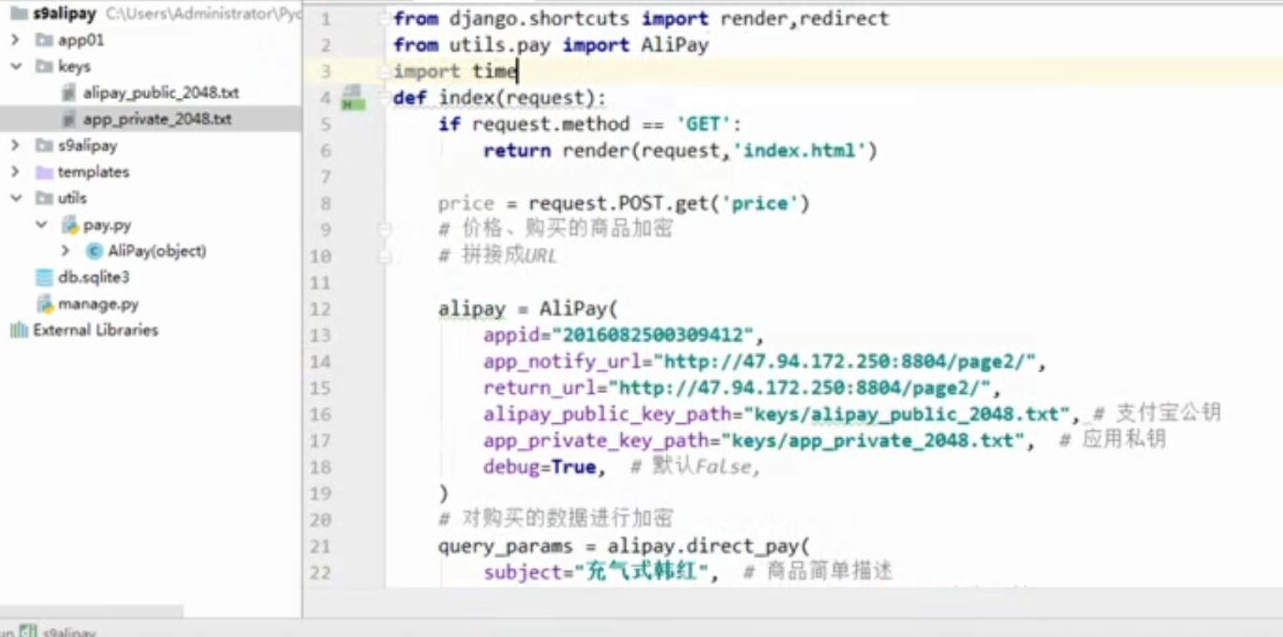
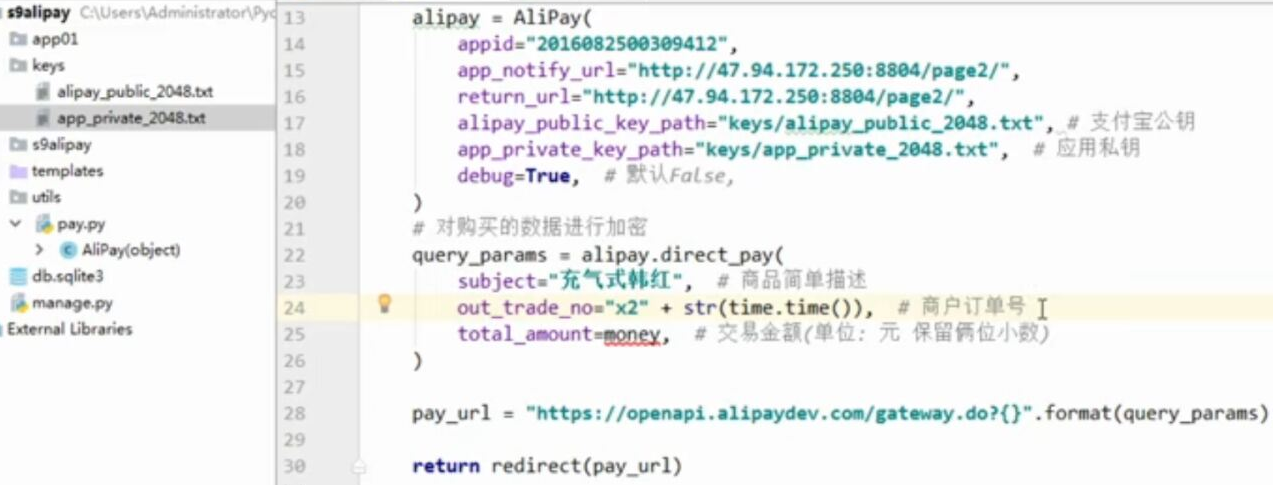
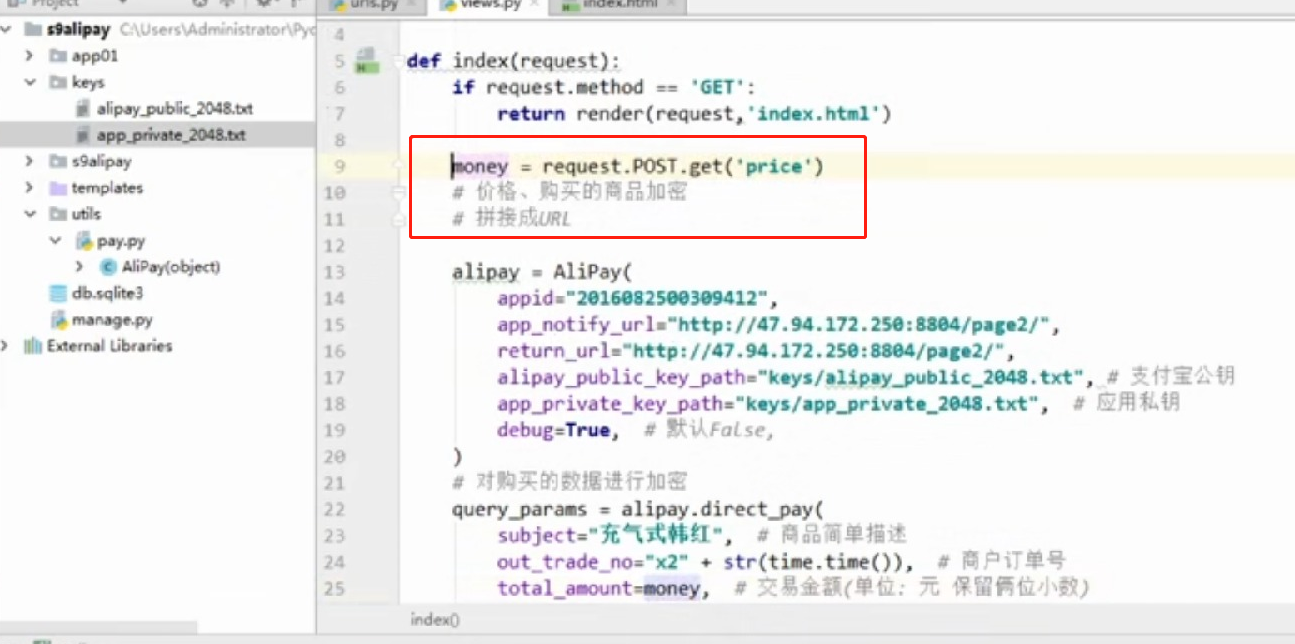
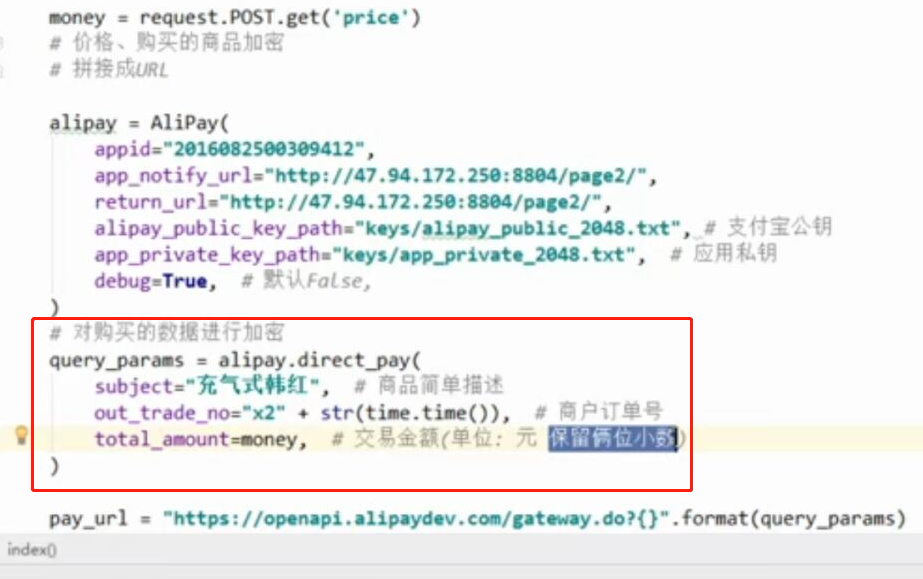
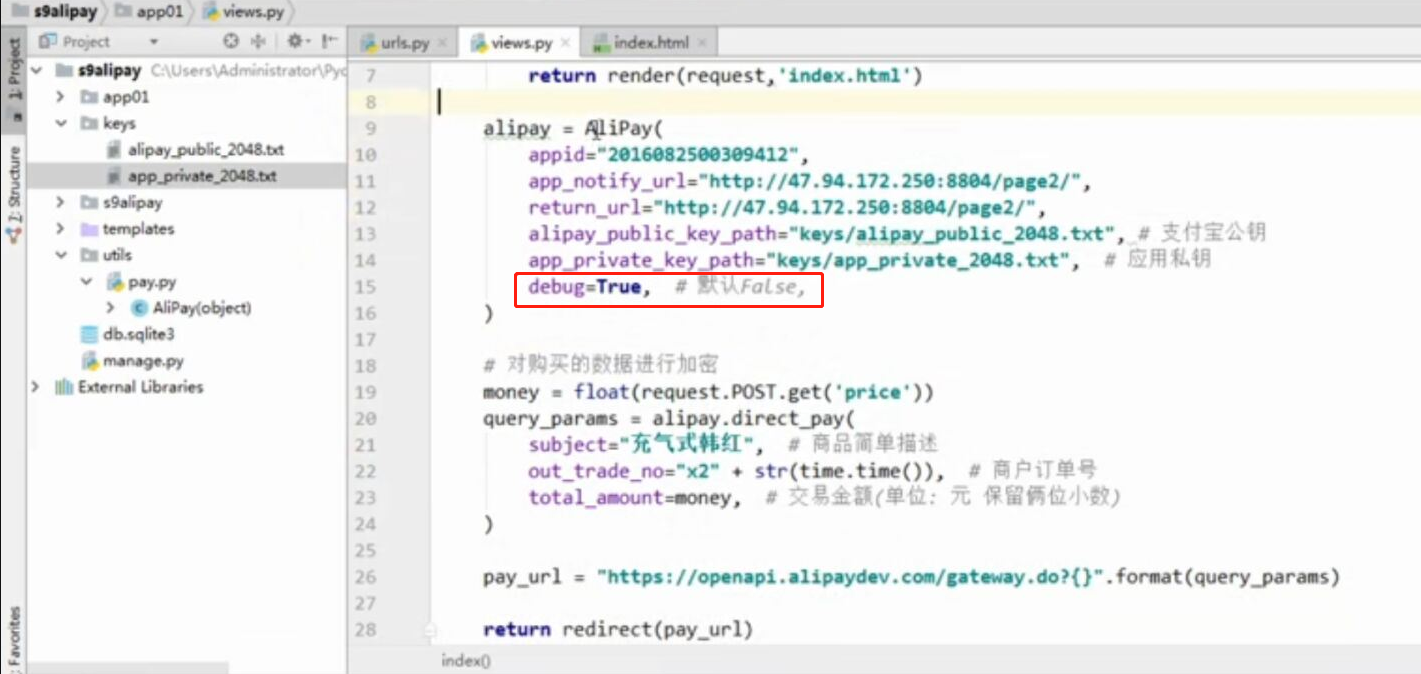
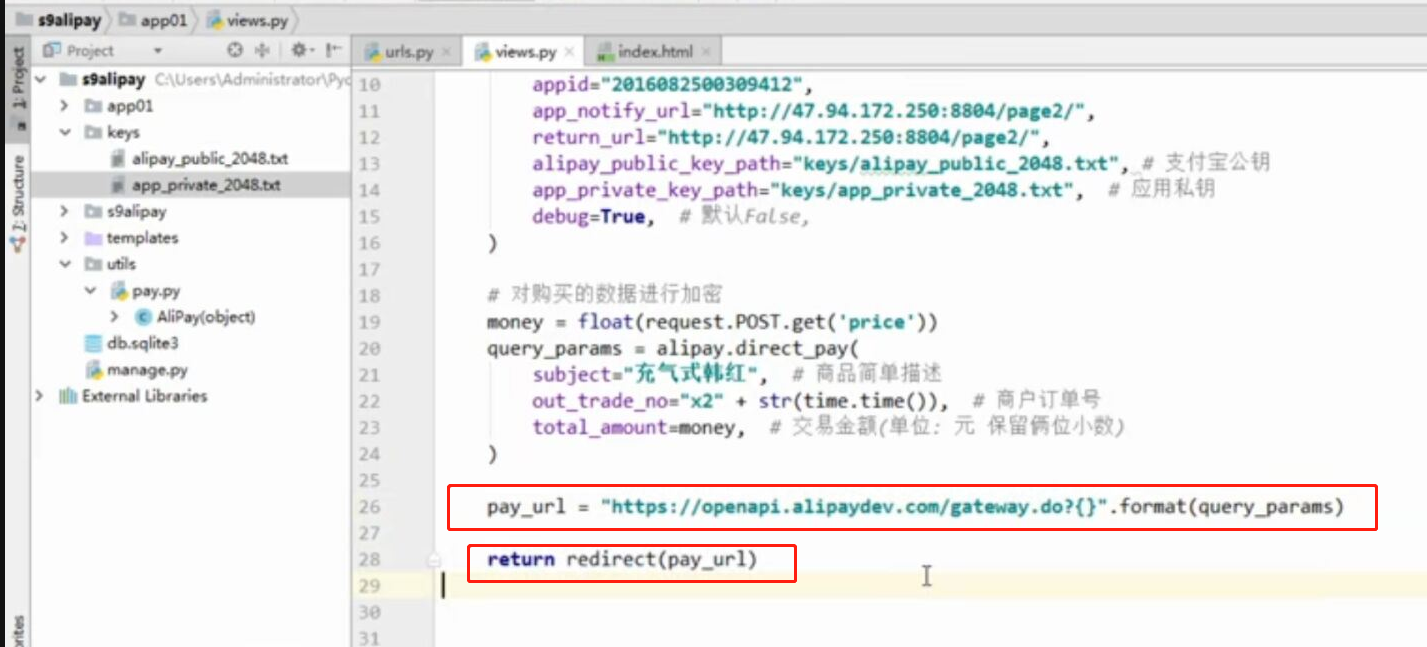
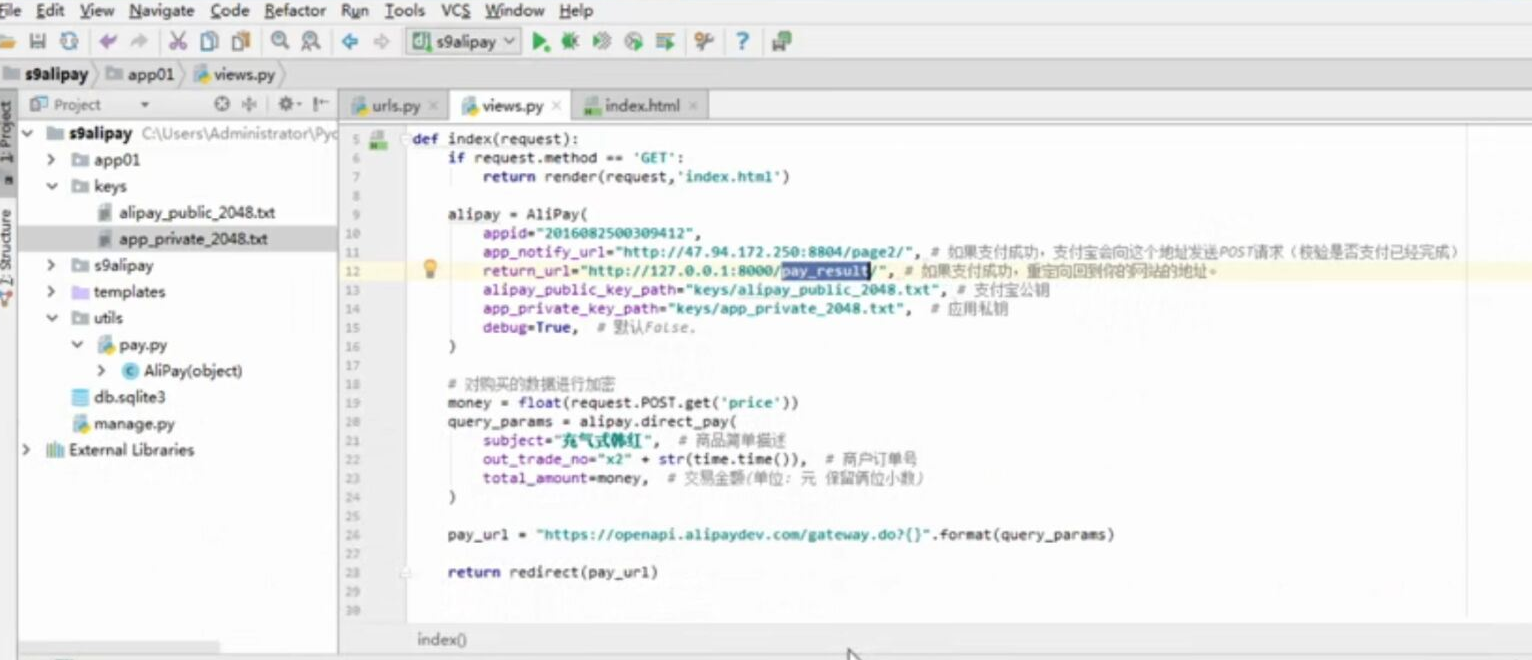
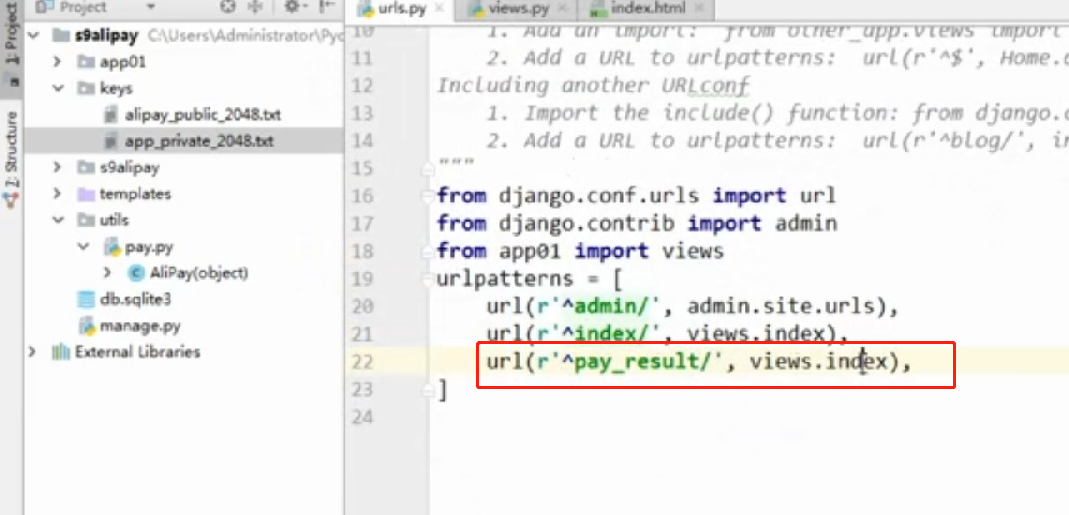
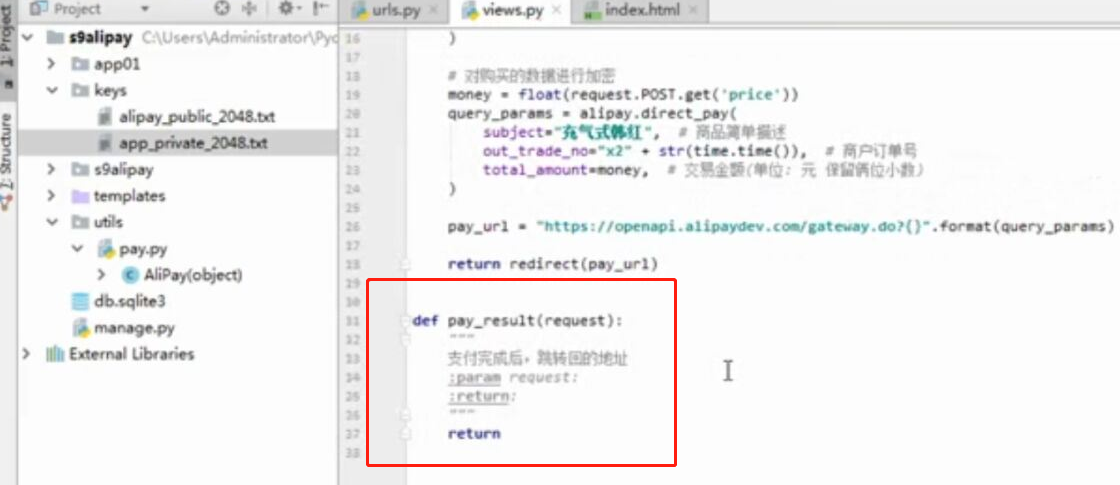
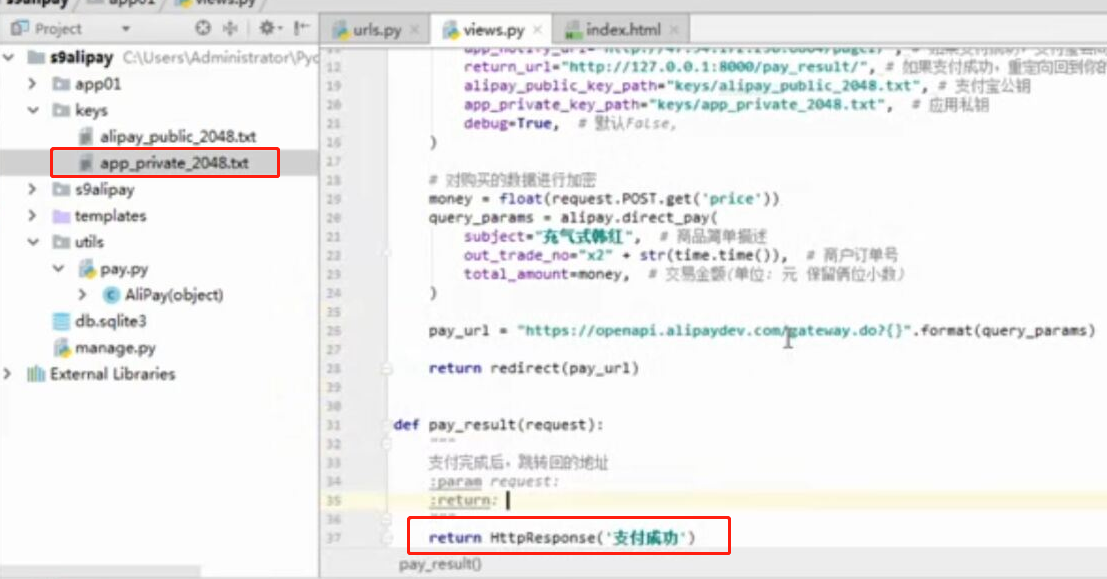
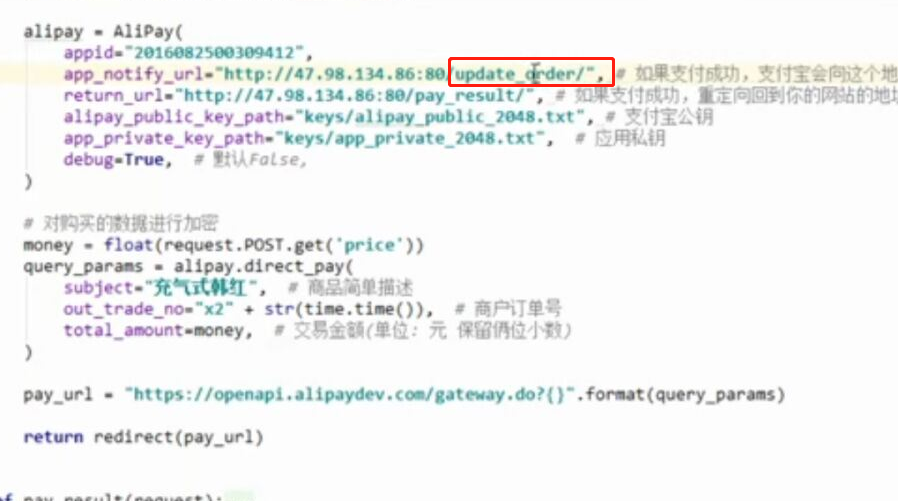
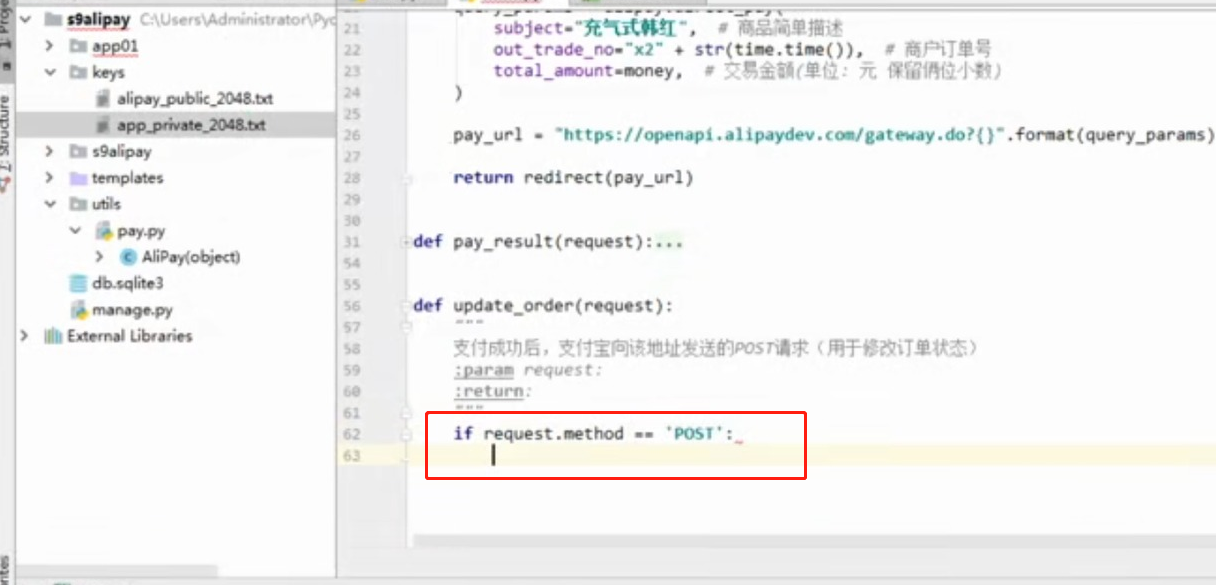
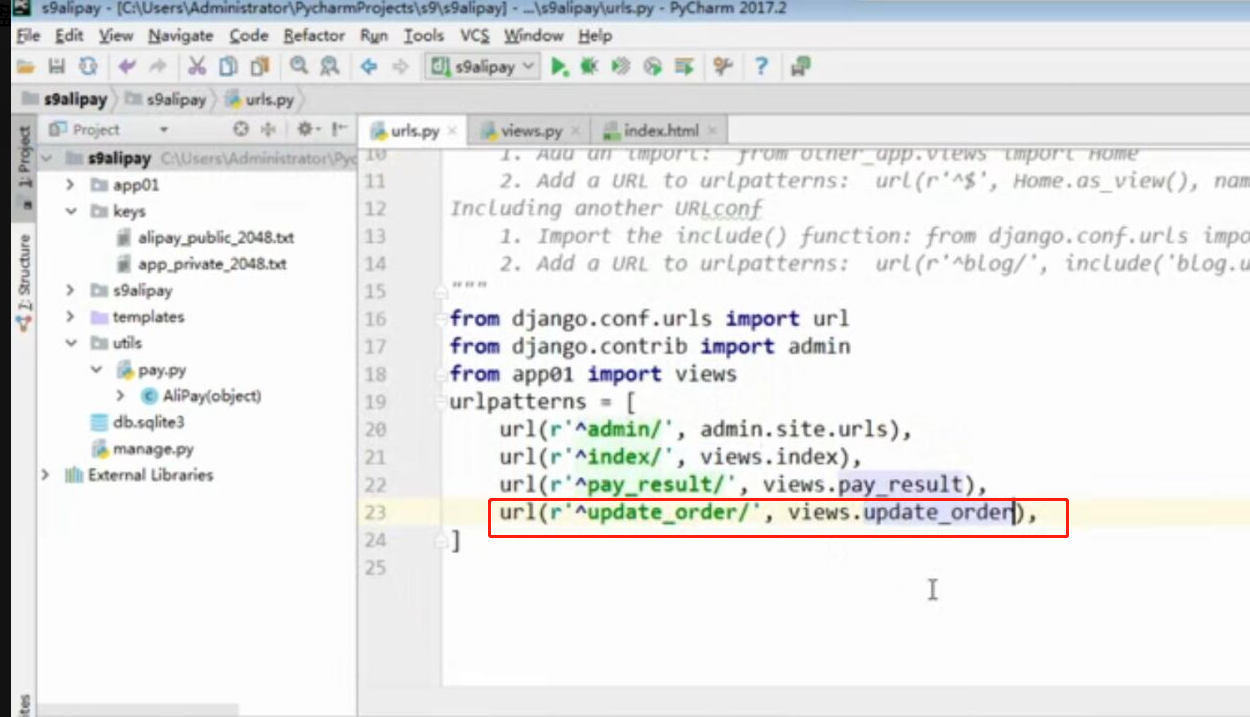
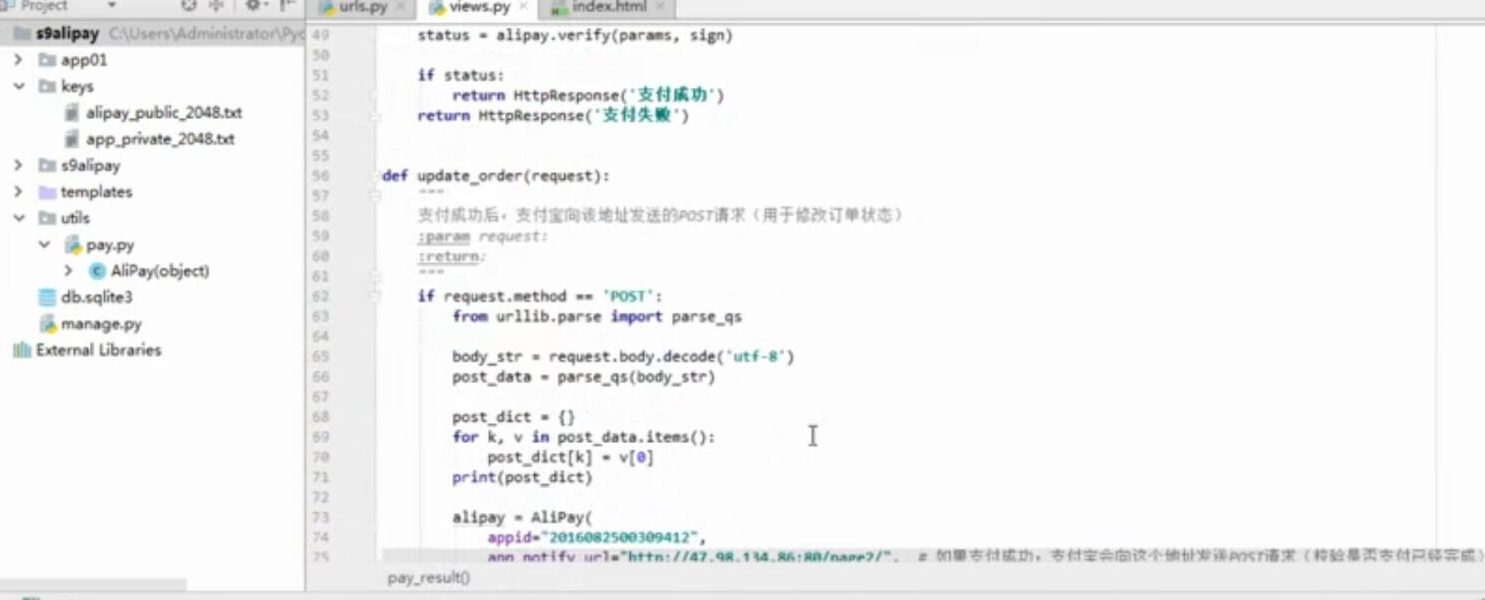
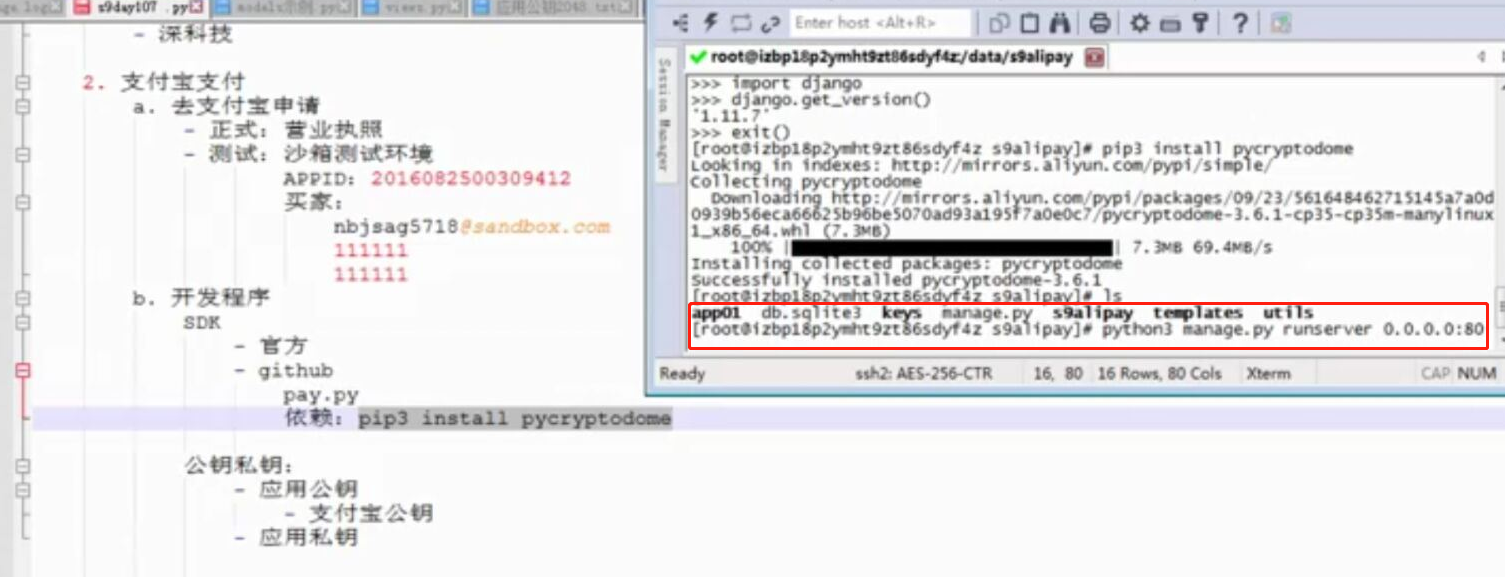
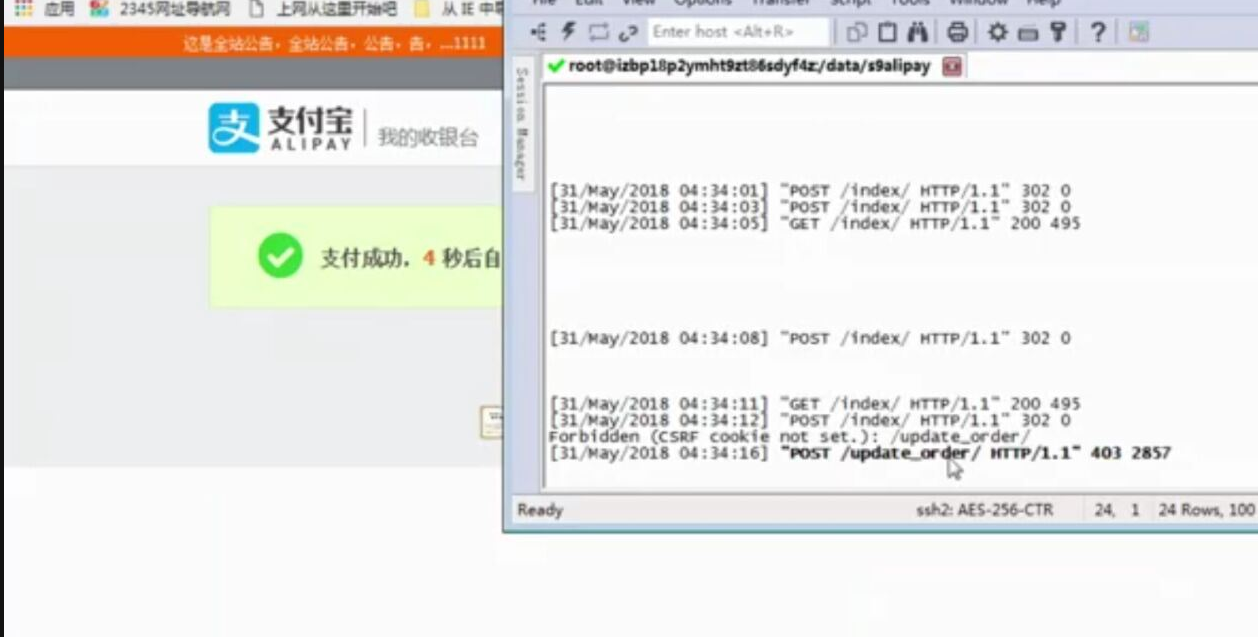
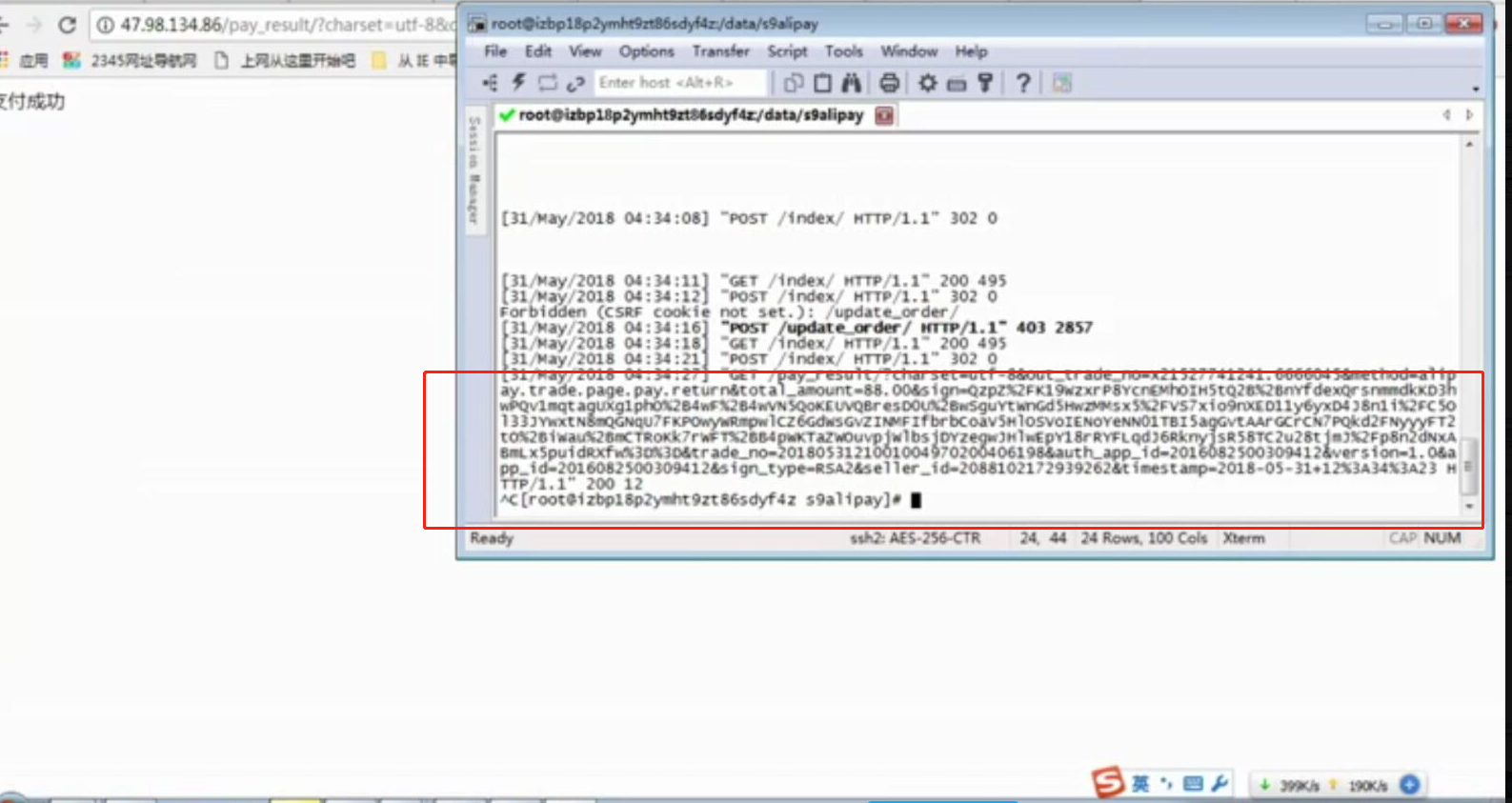
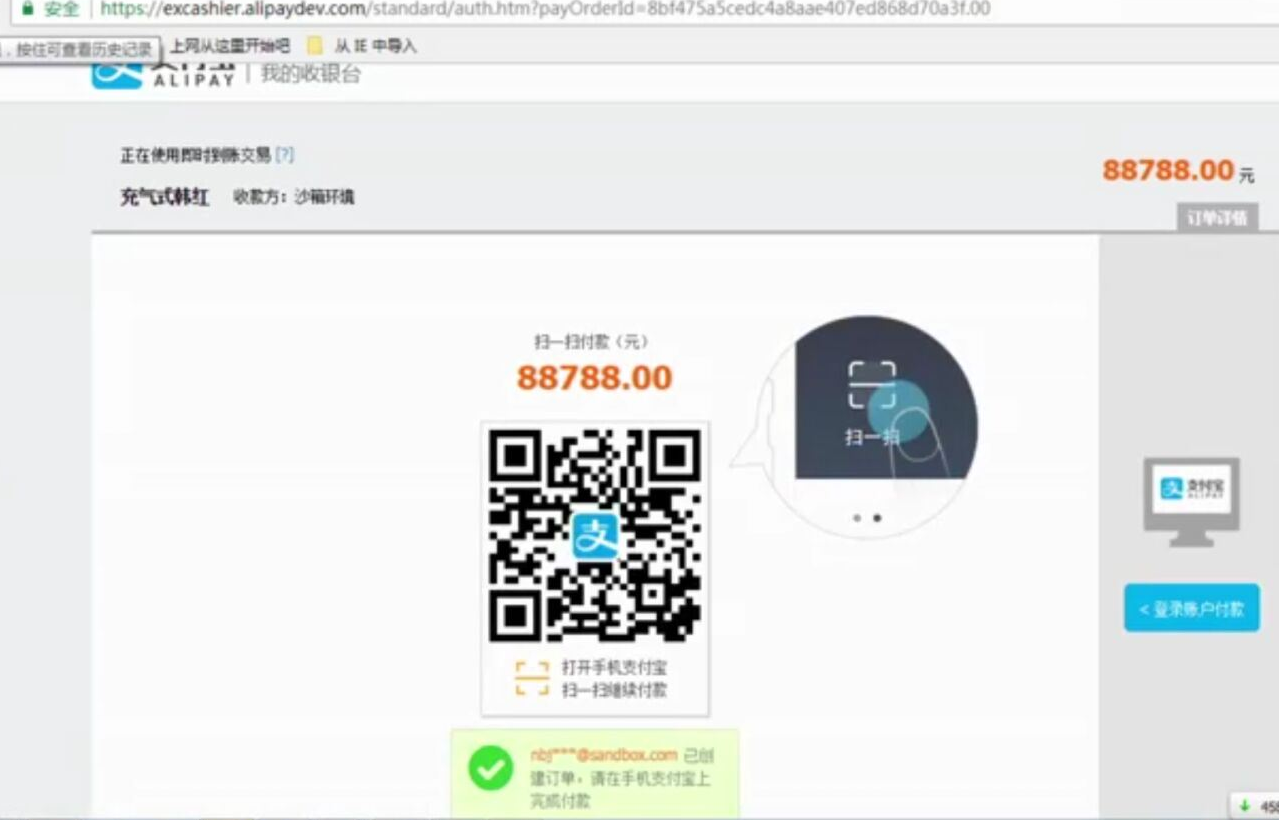
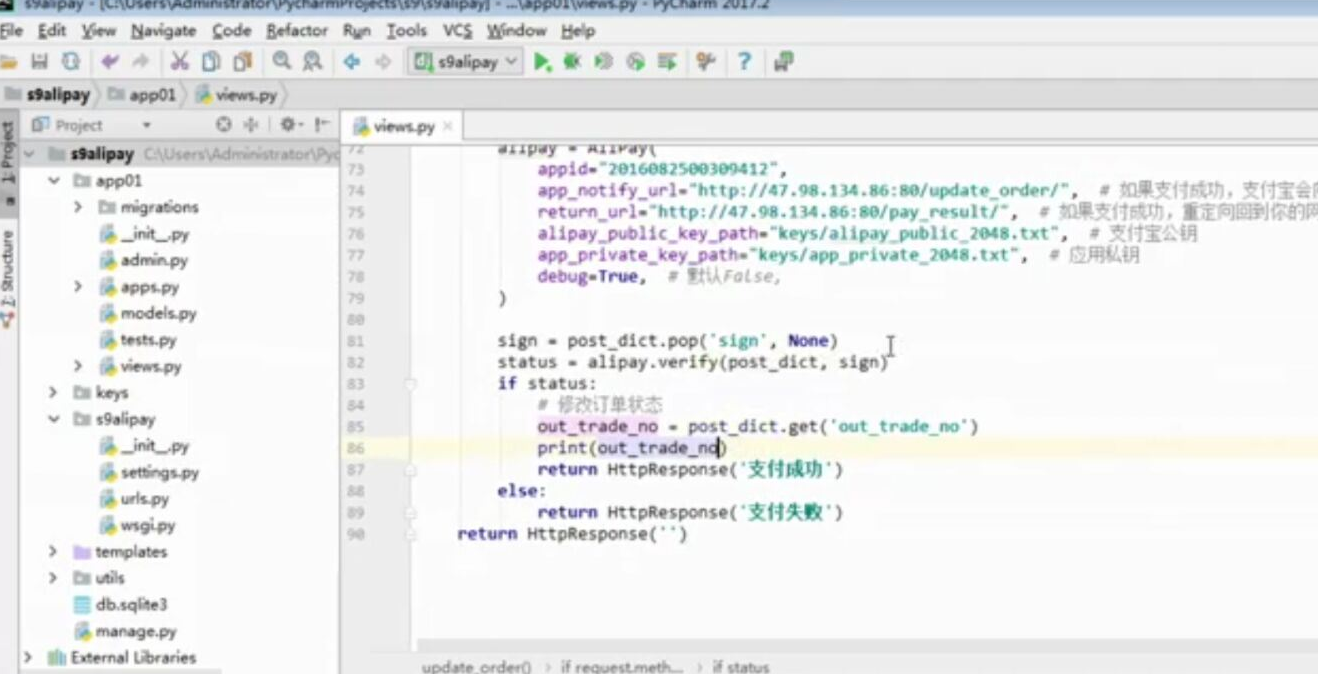
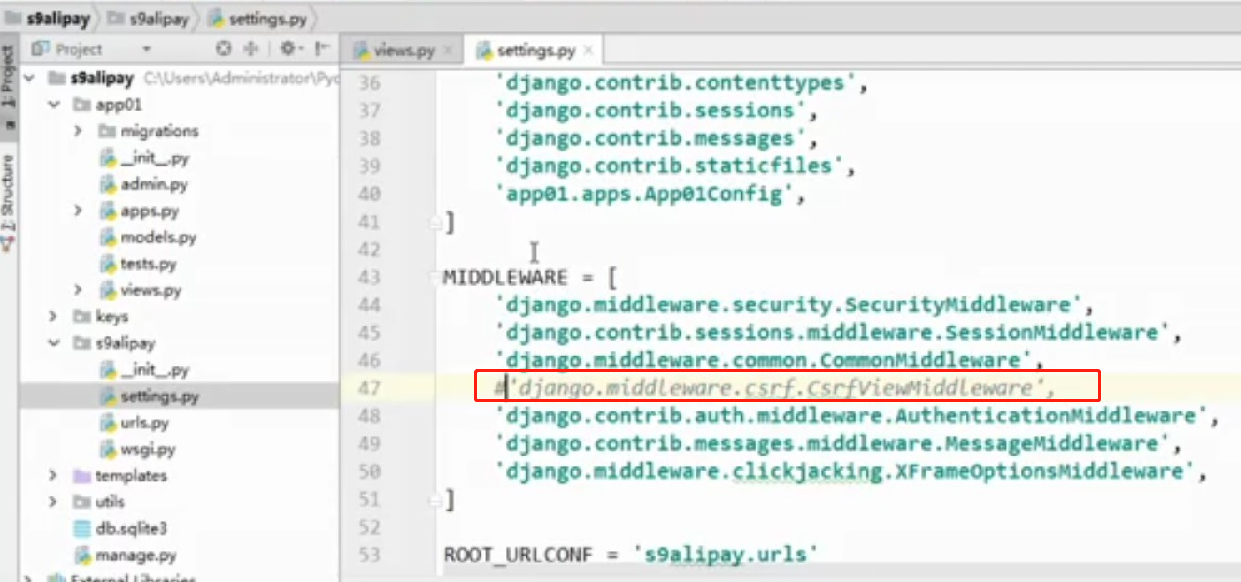
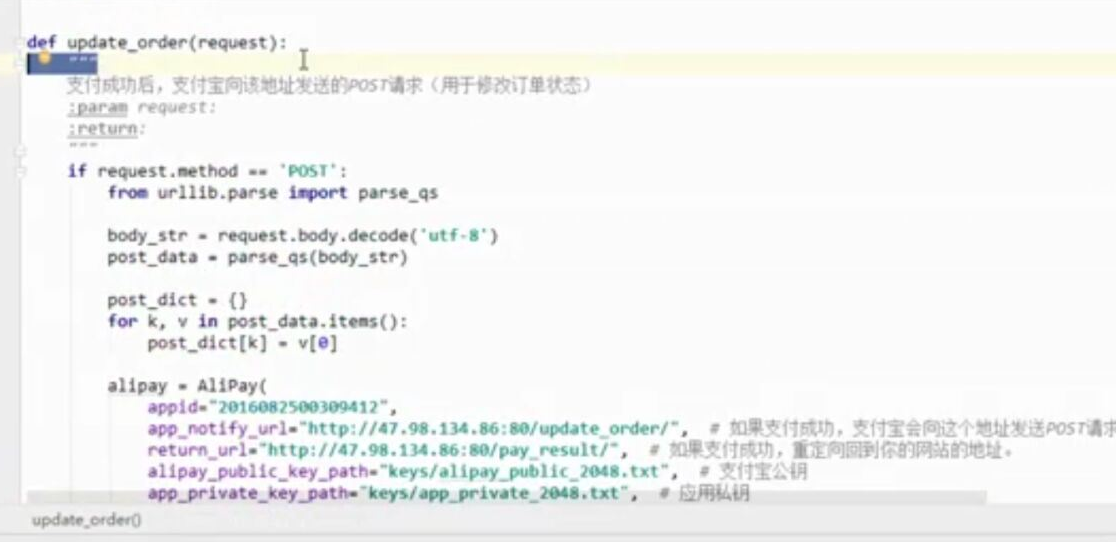
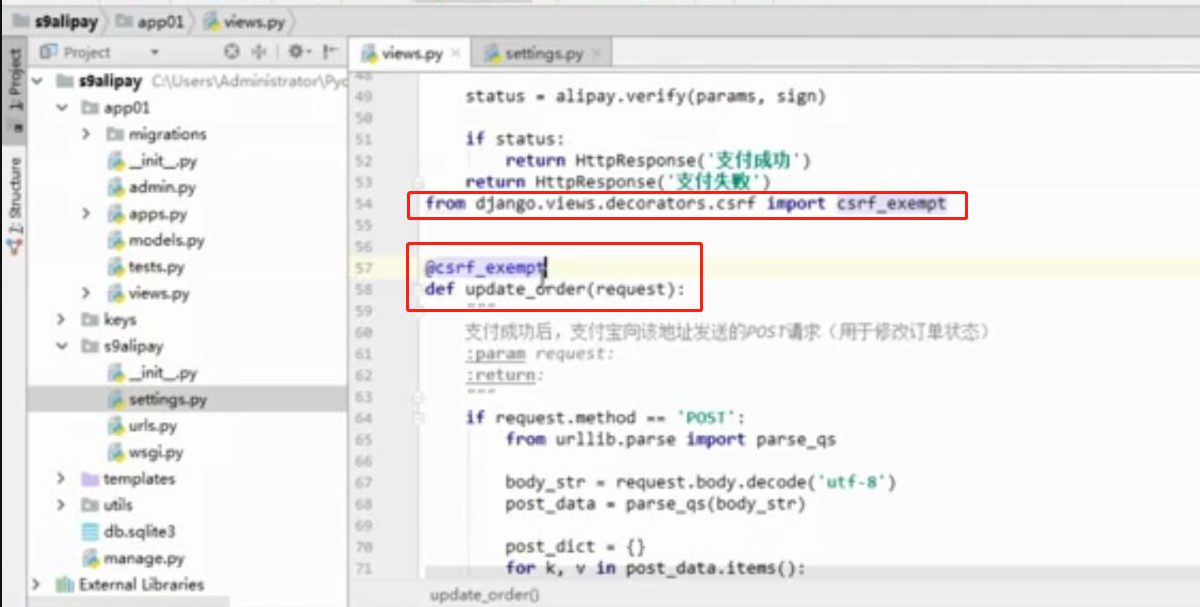
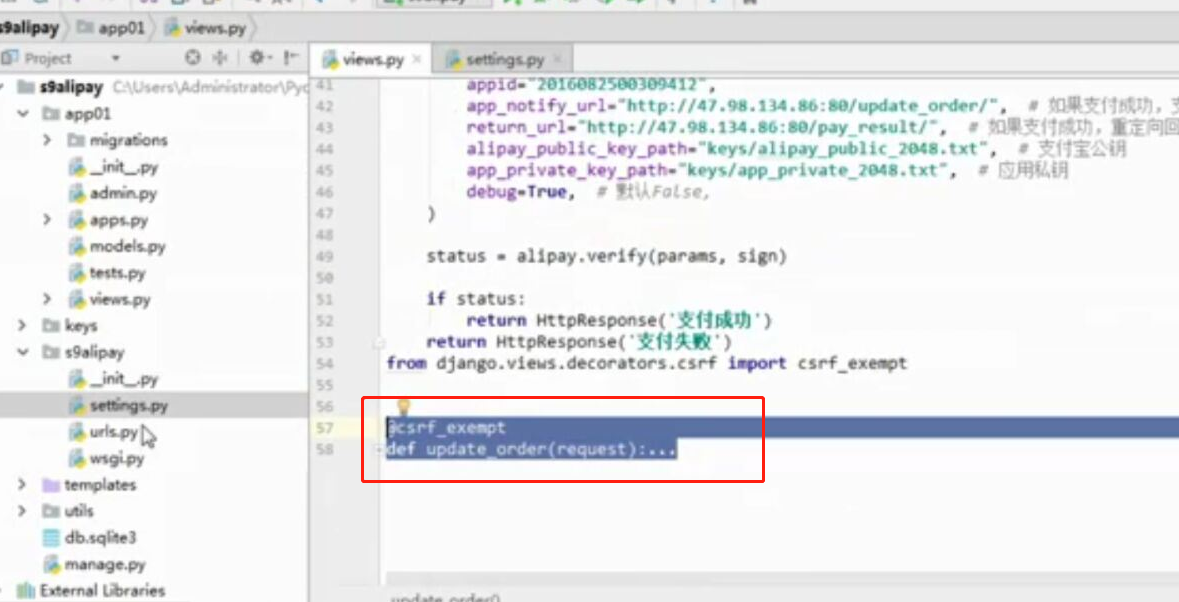
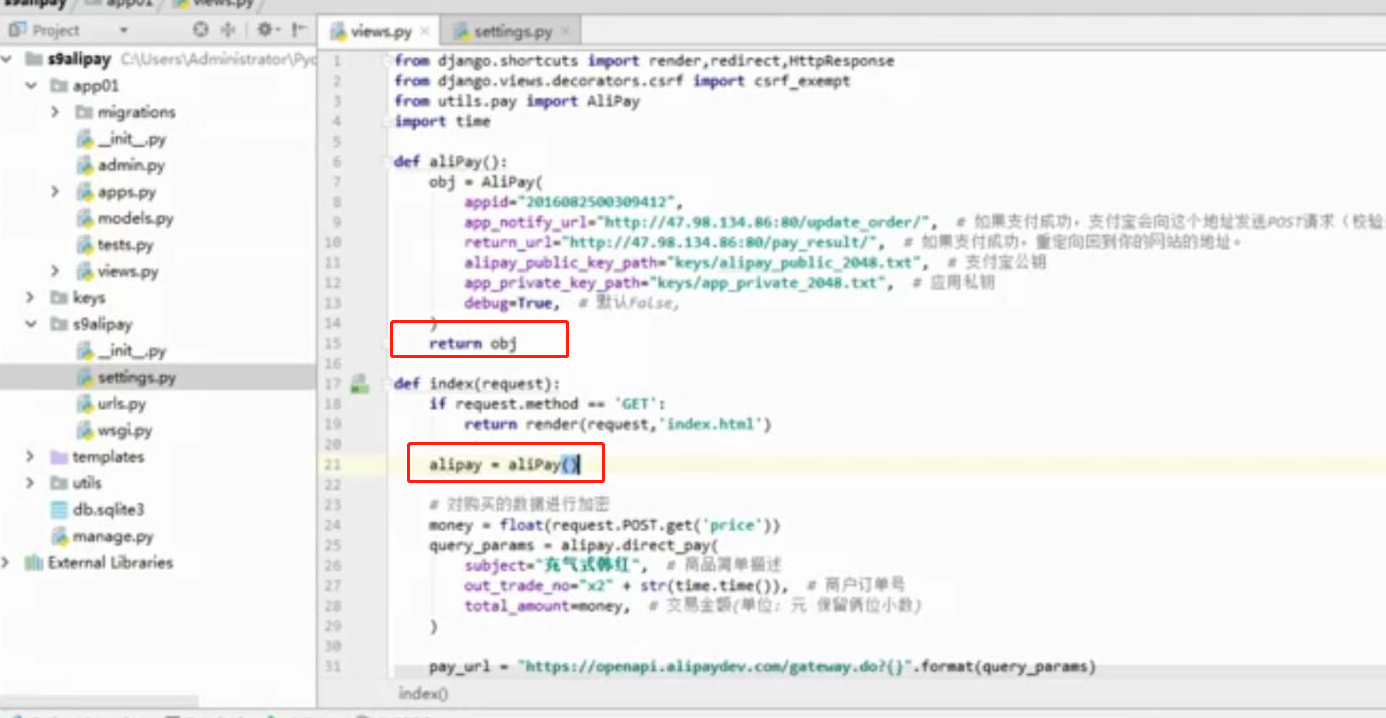
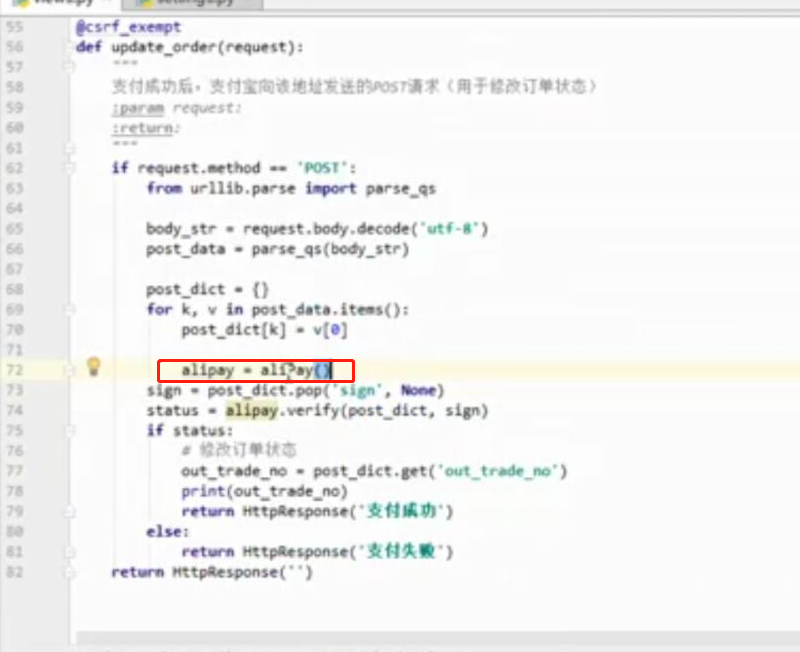
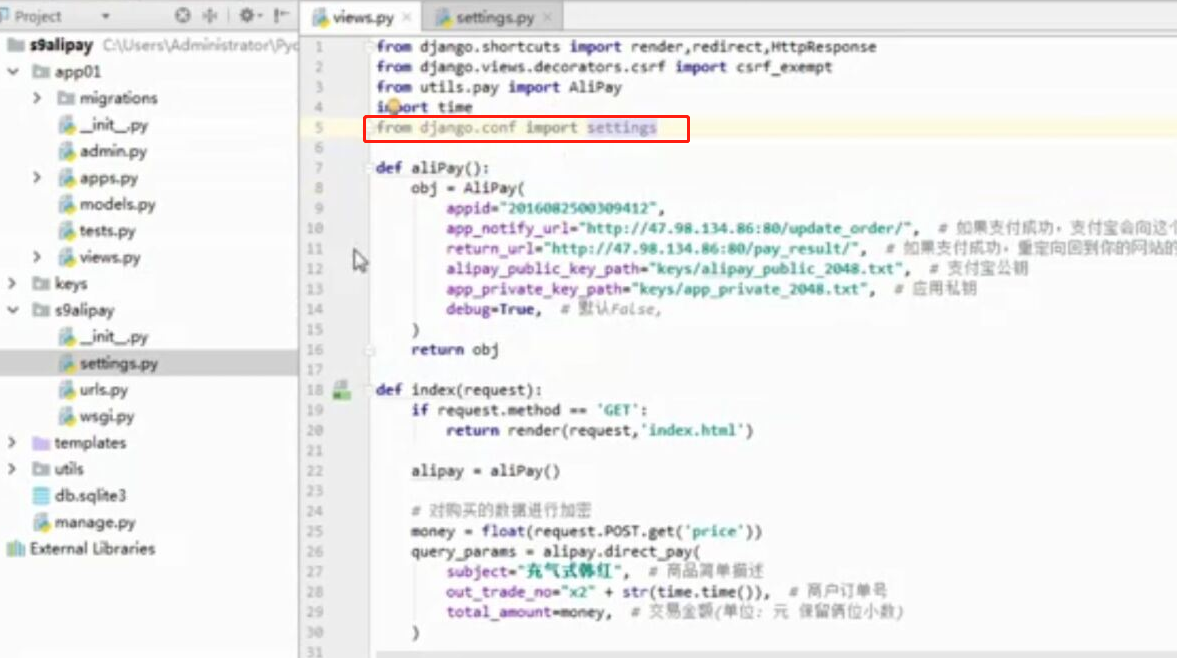
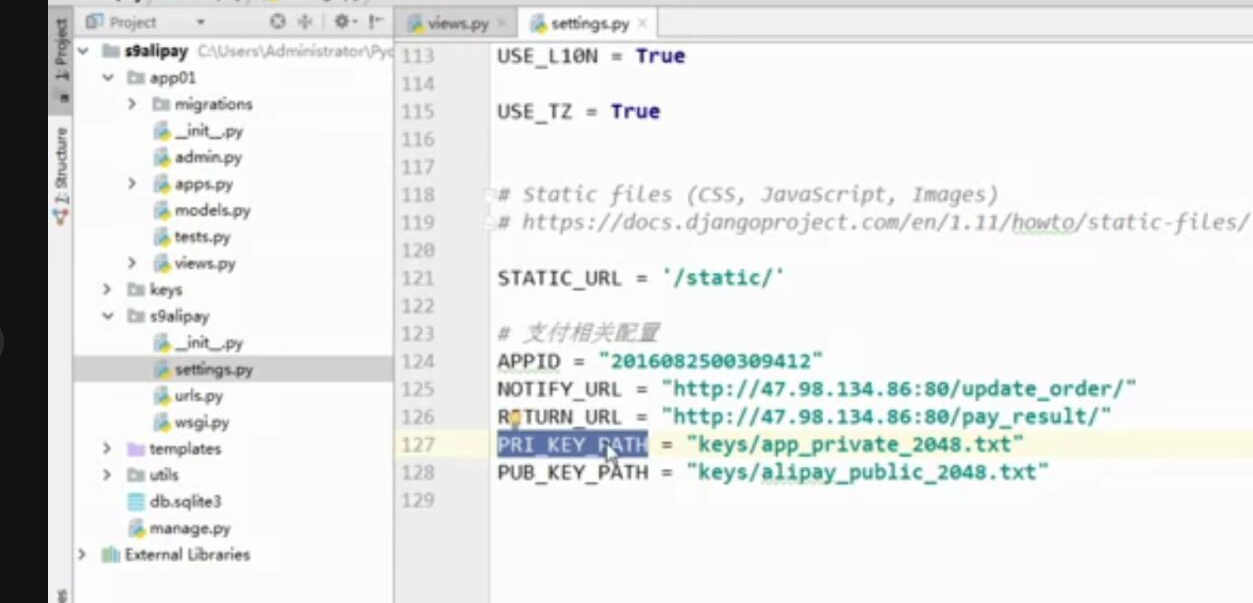
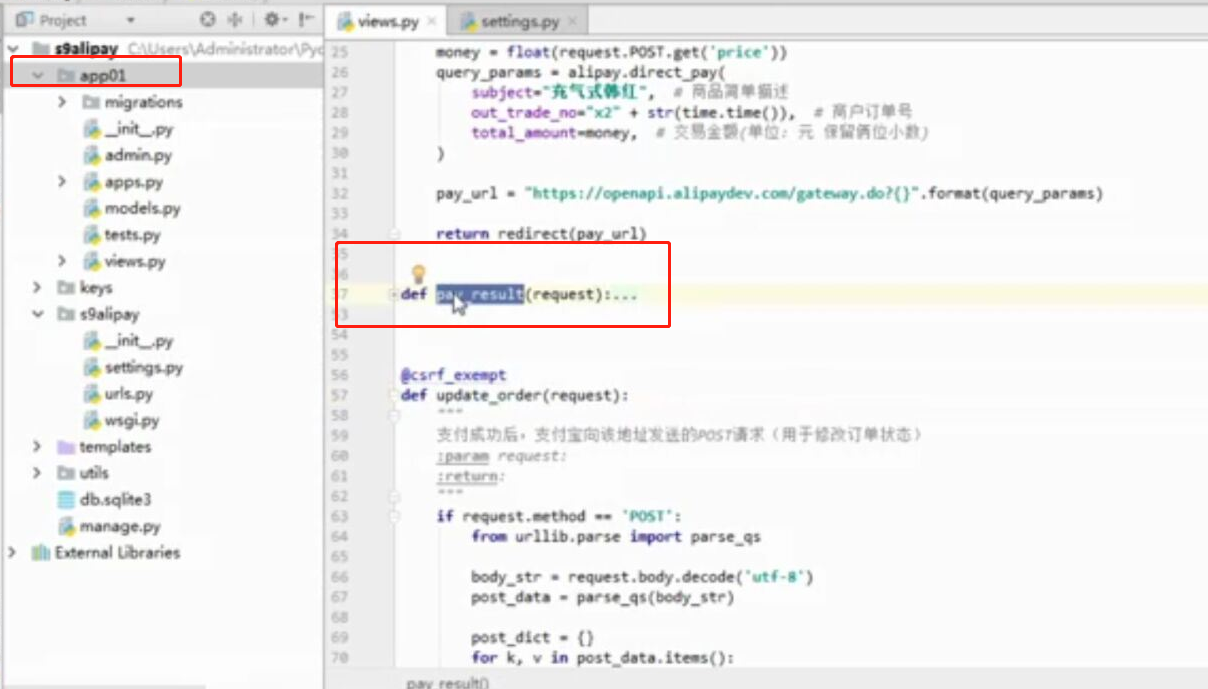
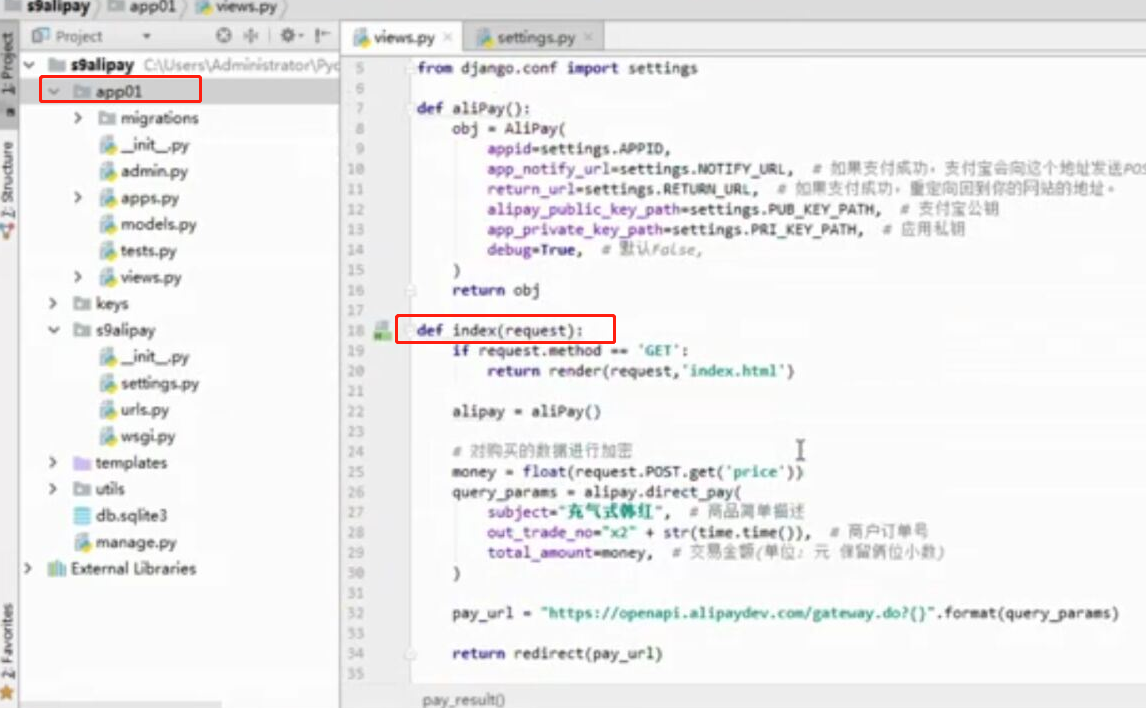
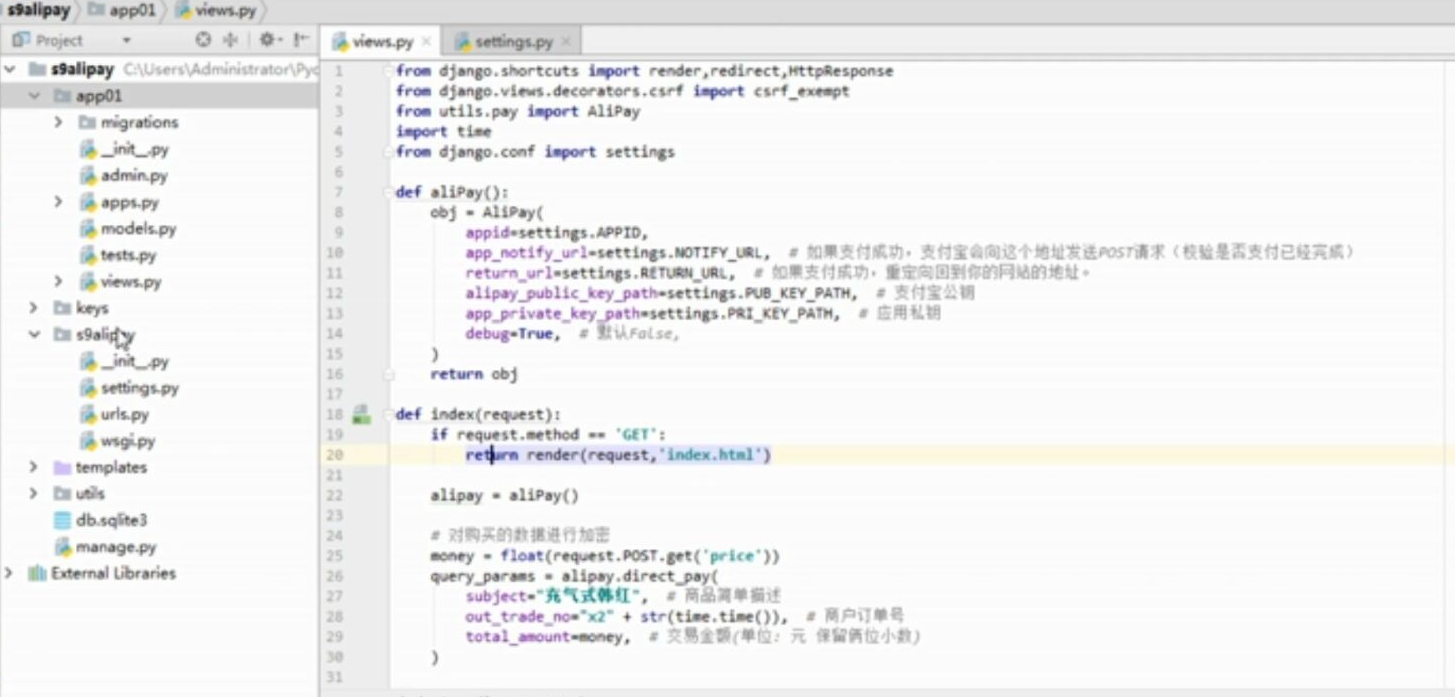
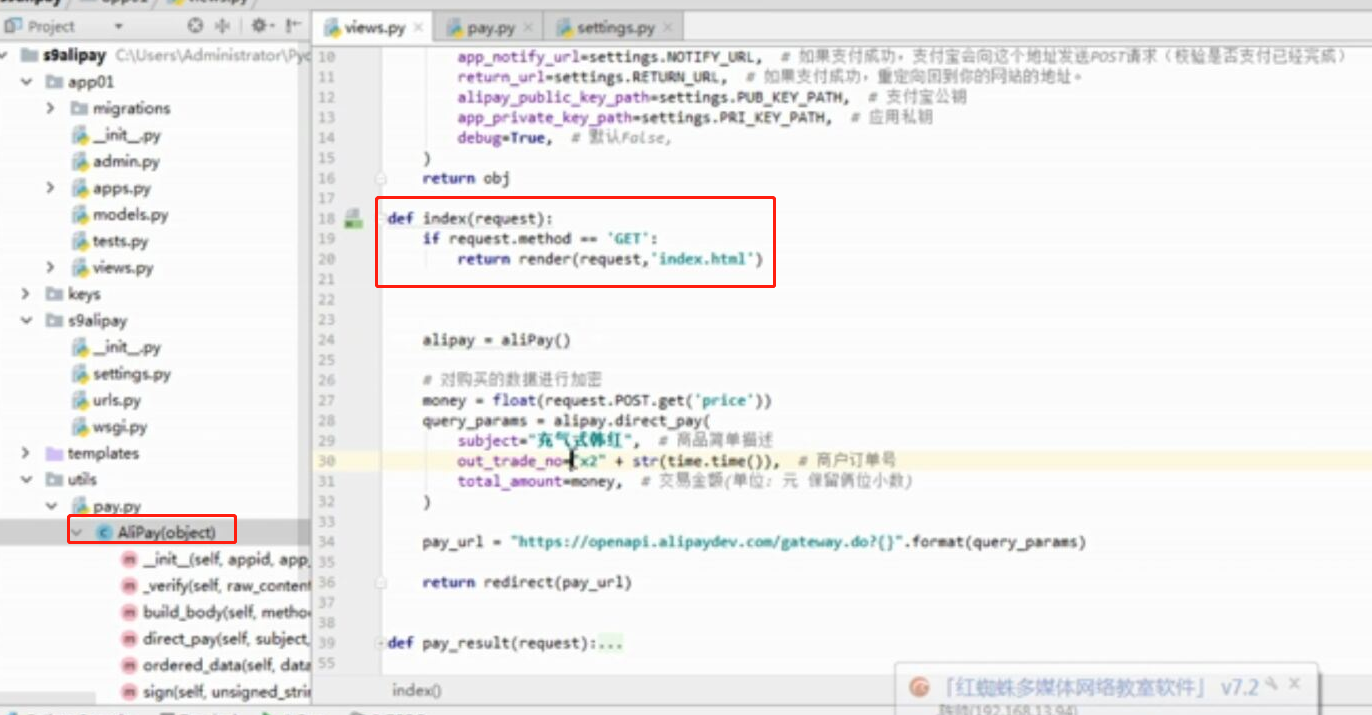
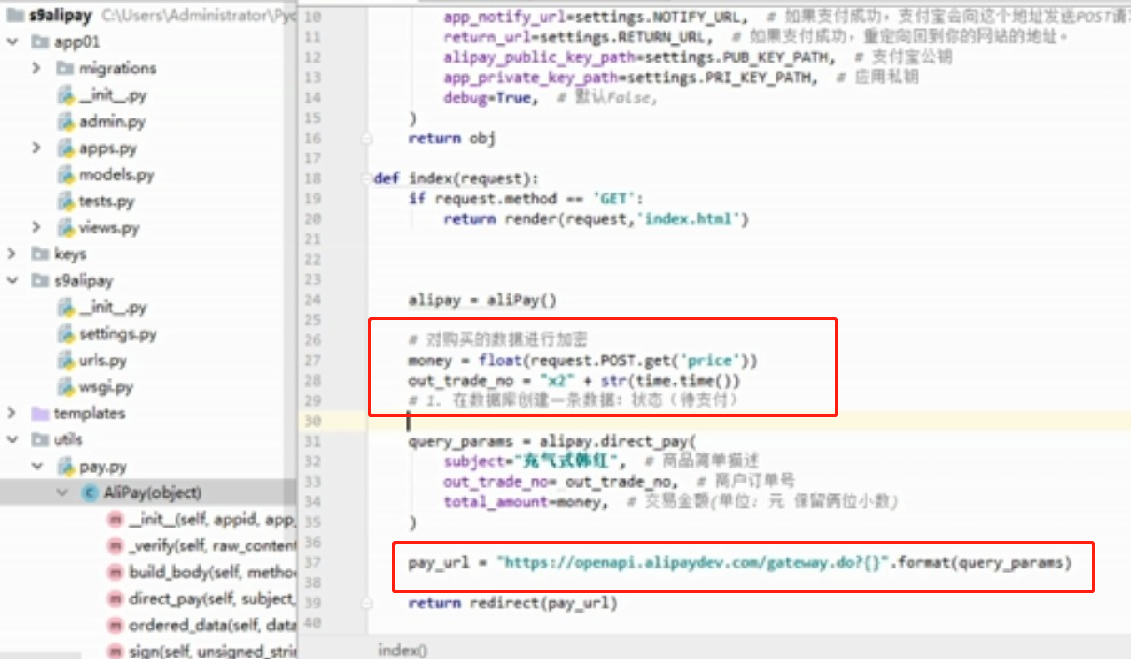
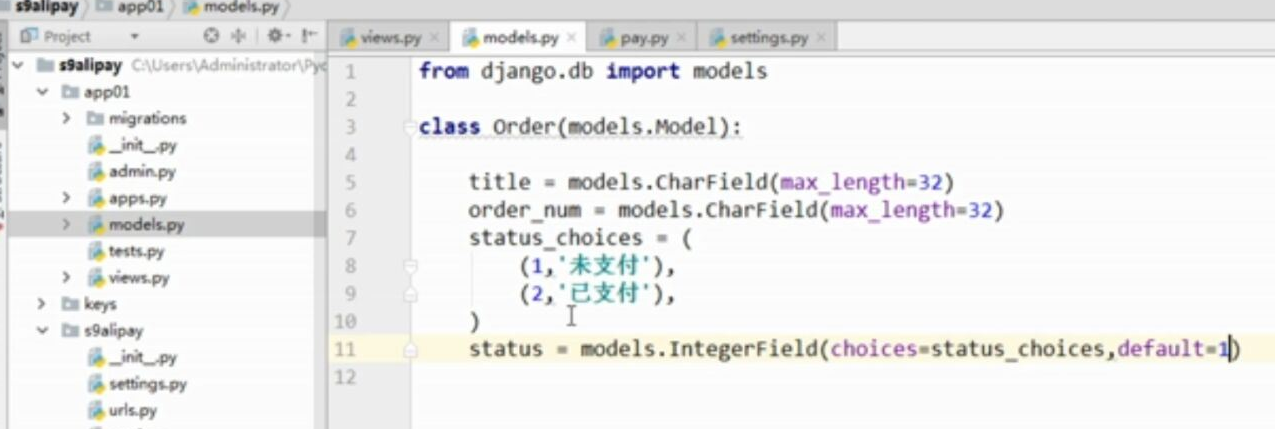
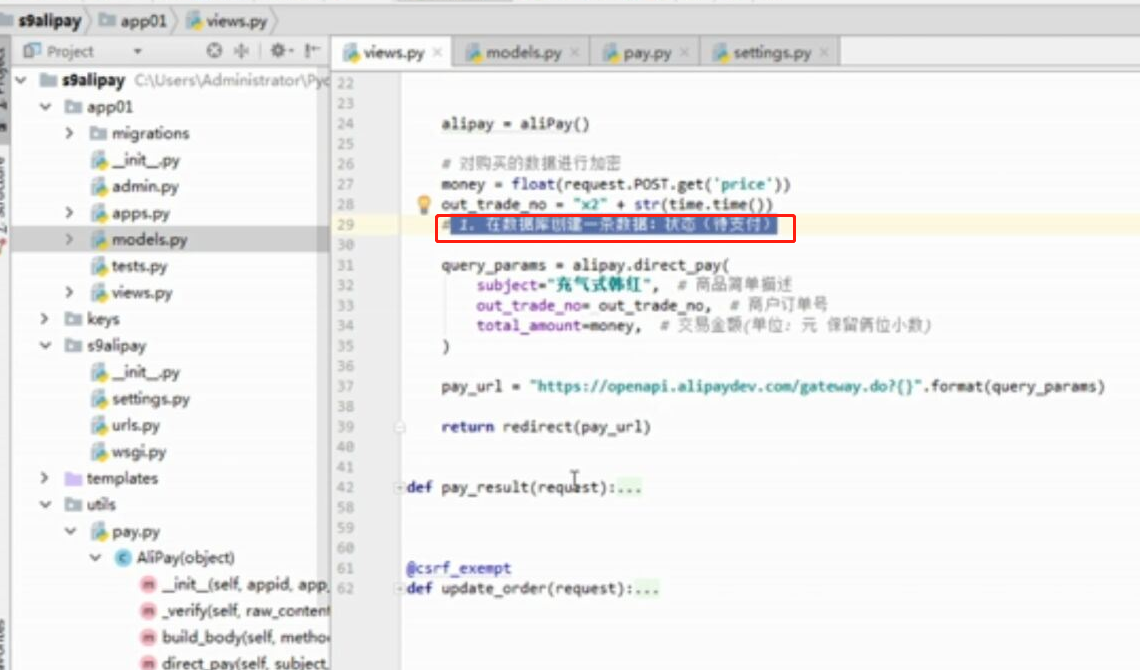
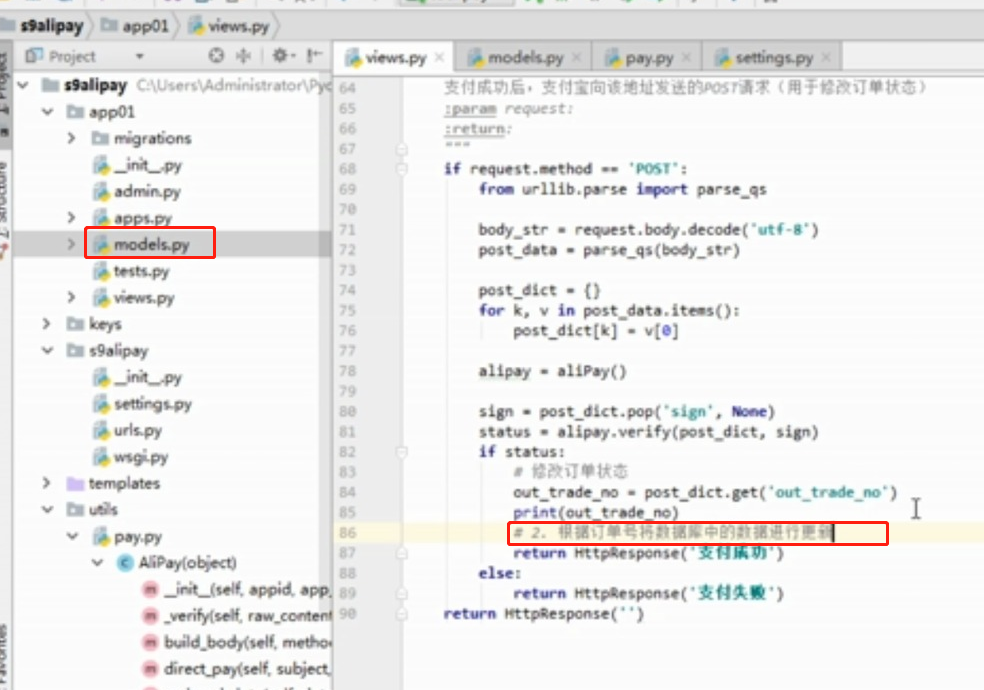
- 基于python-django框架的支付宝支付案例
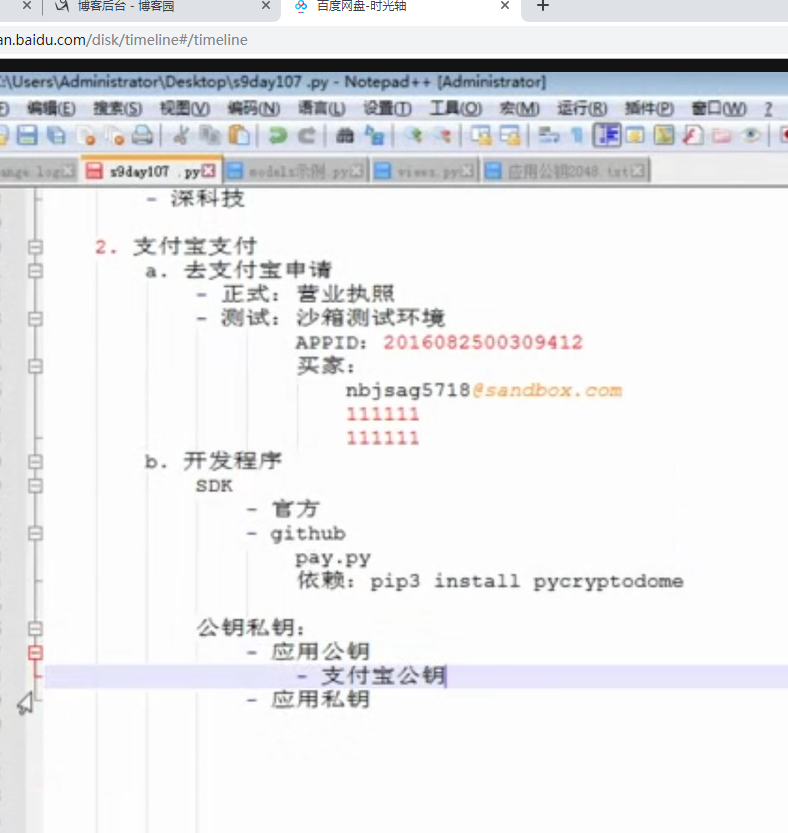
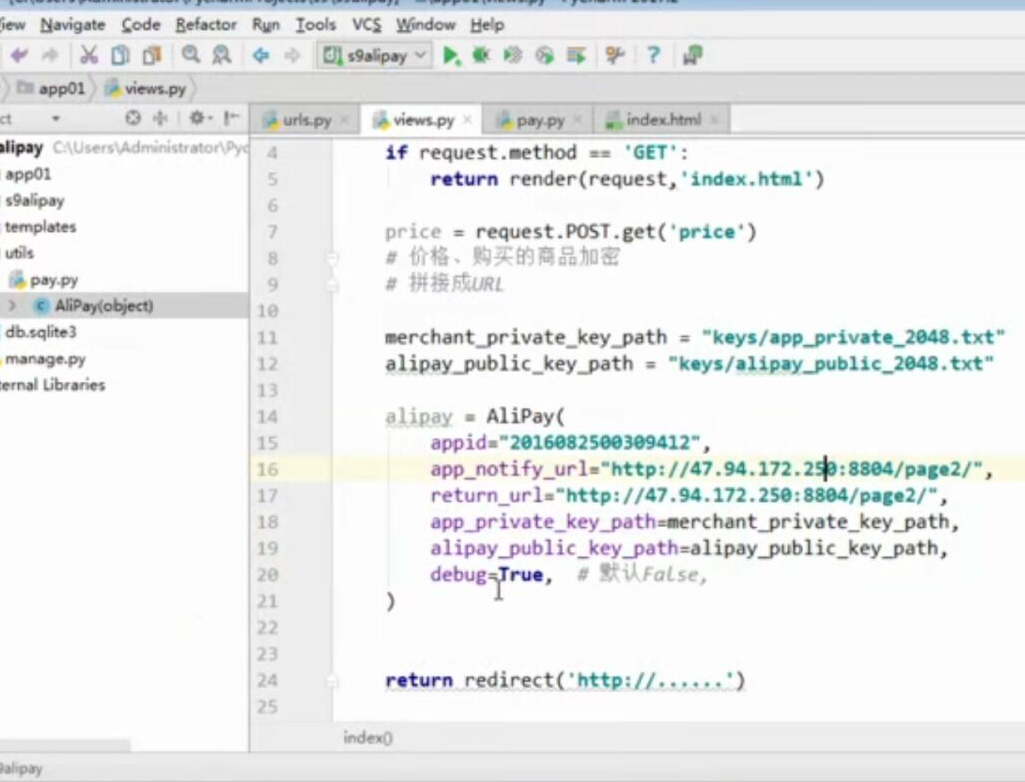
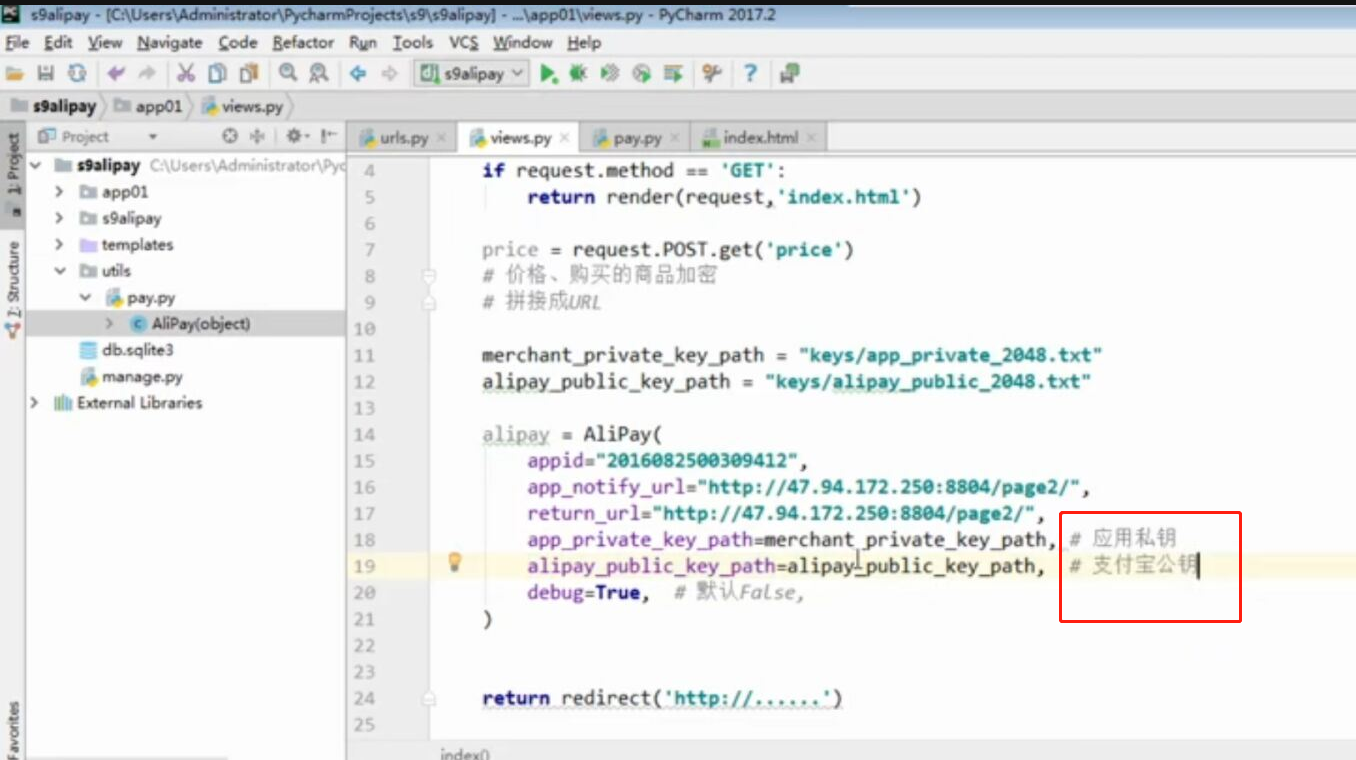
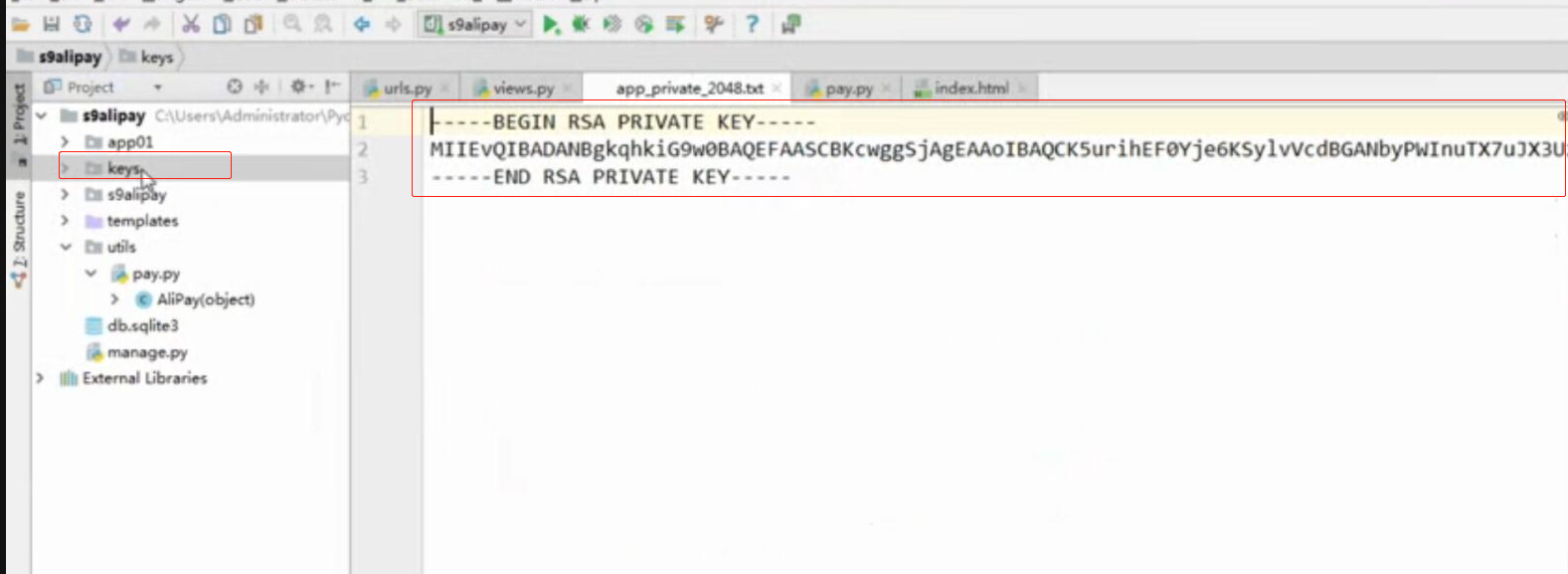
目录 @ 一. 开发前的准备 1. 必须了解的知识 SDK:软件开发工具包,可以为开发者提供快速开发的工具 沙箱环境:也就是测试环境 支付宝支付金额的精度:小数点后两位(面试) 支付宝用的什么加密方式 ...
- IOS开发--支付宝支付
前言:继上次<IOS开发--微信支付>以来,一直没有太多时间,更新总结详细支付这样的长篇大论,很抱歉.今天,推出支付宝支付的详细流程. 1.开始下载和查看支付宝支付的Demo. 我们直接进 ...
- thinkphp5.0 微信公众号接入支付宝支付
---恢复内容开始--- 真是无力吐槽这个需求了,想骂客户,好端端的非要在微信公众号接入支付宝,都知道微信公众号是拒绝支付宝的,屏蔽了支付宝,所以在微信公众号接入支付宝的话就必须手动复制链接跳出微信内 ...
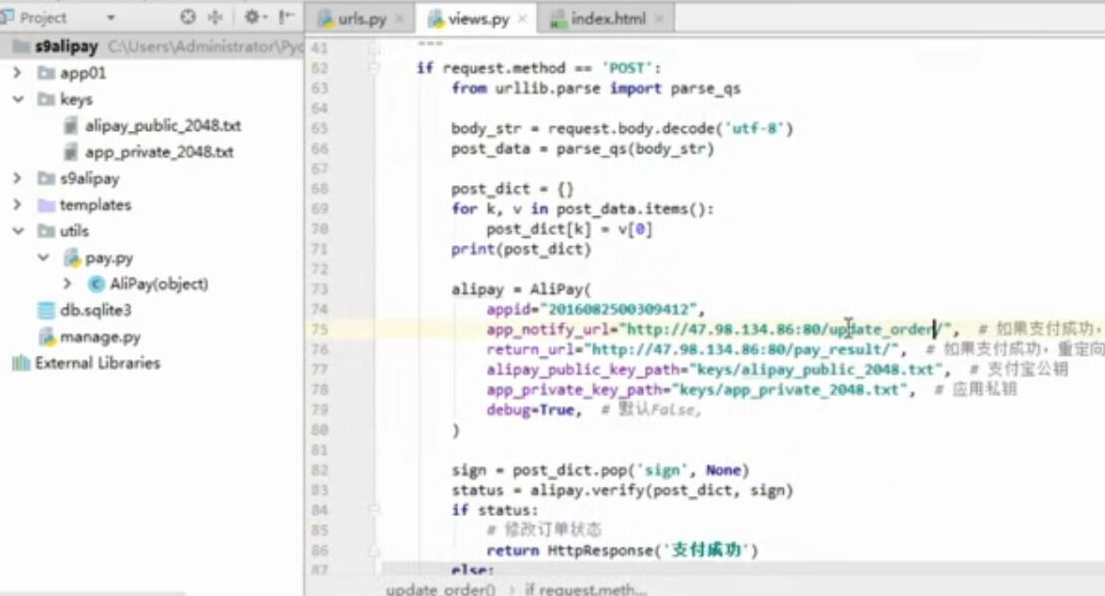
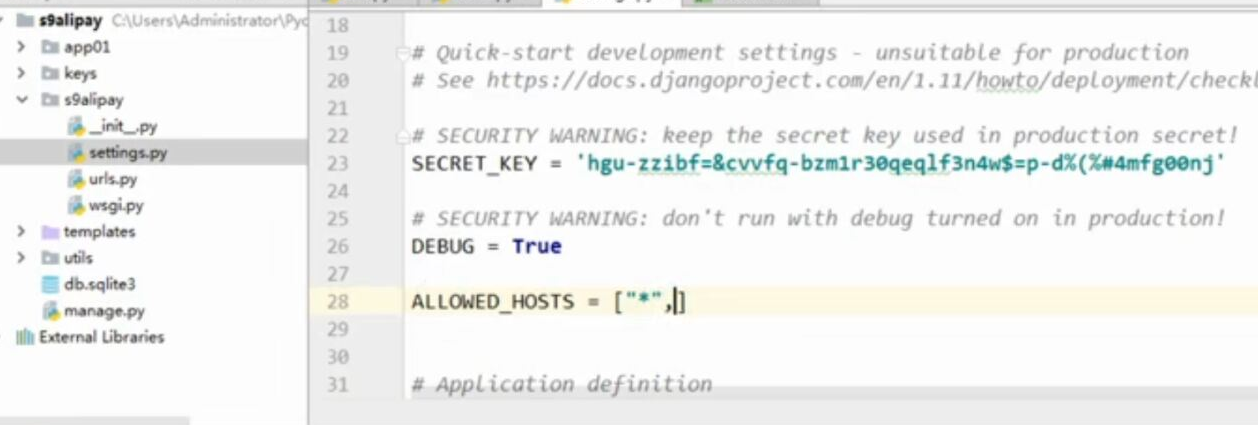
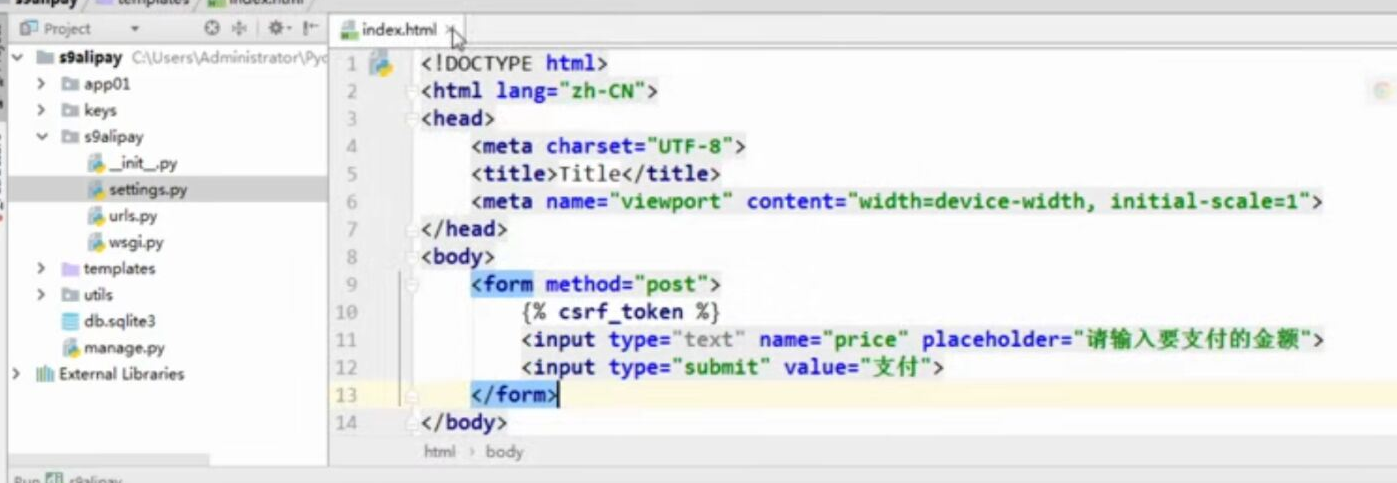
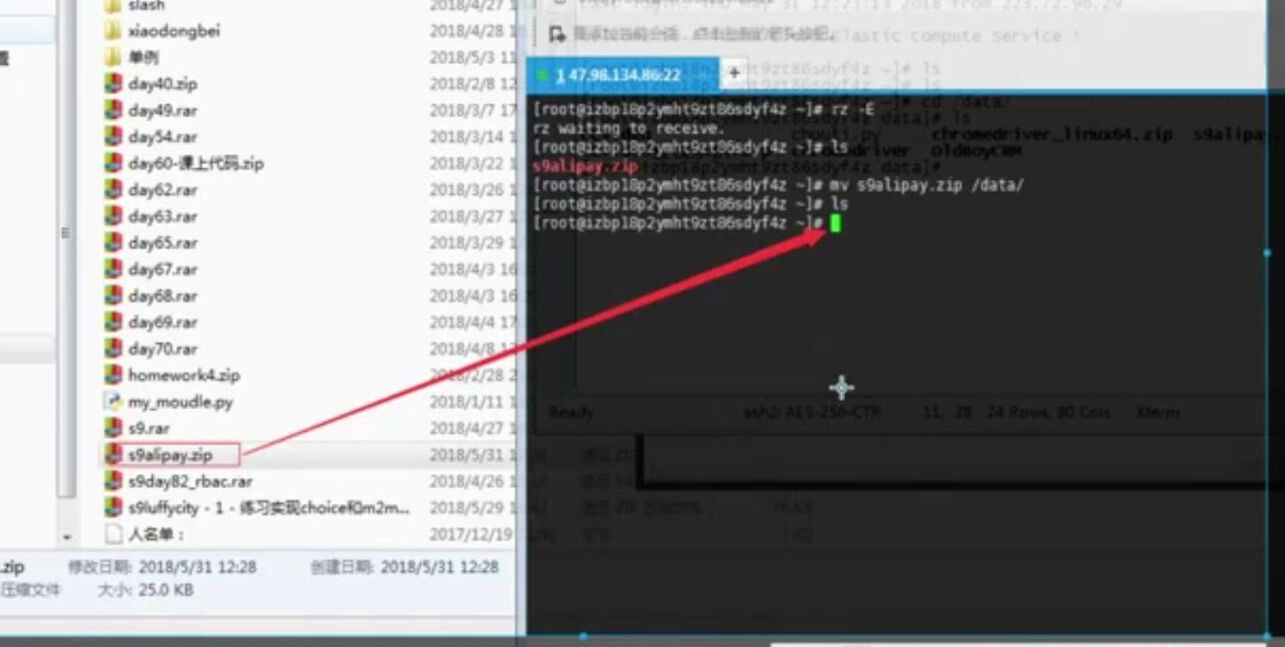
- Django 对接 支付宝支付, 回调
平台 点击这里进入 蚂蚁金服开放平台 沙箱 点击这里进入 沙箱环境 初始界面 设置公钥 下载创建秘钥工具 1. 进入文档中心 这里 2. 选中 电脑网站支付 3. 进入后选中 API 列表 中的 统 ...
- 使用Tornado异步接入第三方(支付宝)支付
目前国内比较流行的第三方支付主要有支付宝和微信支付,博主最近研究了下如何用Python接入支付宝支付,这里我以Tornado作为web框架,接入支付宝构造支付接口. 使用Tornado异步接入支付宝支 ...
- 支付宝支付之App支付
与微信支付对比,支付宝支付就没有那么多坑了,毕竟支付宝开放平台的文档还是描述的很详细的. 支付宝开放平台地址:https://docs.open.alipay.com/204/105297/ 支付宝支 ...
随机推荐
- PHP 生成公钥私钥,加密解密,签名验签
test_encry.php <?php //创建私钥,公钥 //create_key(); //要加密内容 $str = "test_str"; //加密 $encrypt ...
- Bean配置
1.xml配置(摘抄自:https://www.cnblogs.com/zyx1301691180/p/7665971.html) 一.setter方法配置Bean: 1.创建一个 Spring Be ...
- EAFP vs LBYL
EAFP vs LBYL 检查数据可以让程序更健壮,用术语来说就是防御性编程.检查数据的时候,有EAFP和LBYL两种不同的编程风格,具体的意思如下: LBYL: Look Before You Le ...
- AS3动画效果常用公式
缓动公式: sprite.x += (targetX – sprite.x) * easing;//easing为缓动系数变量 sprite.y += (targetY – sprite.y) * e ...
- Vue使用指南(二)
'''1.指令 ***** 文本指令 属性指令 方法(事件)指令 表单指令 条件指令 循环指令 2.组件 *** 局部组件 全局组件 父子组件间的交互''' 文件指令 <body> < ...
- BUG:WSL 的 ssh server 无法启动
BUG 使用 sudo service ssh start 启动 ssh 服务,提示: * Restarting OpenBSD Secure Shell server sshd Could not ...
- 滤波器算法(2)-最小均方(LMS)
2018.09.09 写的版本 ①残差平方和 ②平方损失函数: ③函数的极值点为偏导数为0的点:(将问题变成一个求极值的问题) ④求解得: matlab代码: ① y=ax+b+e方程 functio ...
- C#操作Windows控制面板
先介绍一下Windows控制面板的一些操作,再介绍如何用C#语言来操作控制面板. 1.如何快速打开控制面板中的项目: 运行输入(大小写不敏感) control system 打开系统信息 contro ...
- 【转】Java基础——面试题汇总
1.JDK 和 JRE 有什么区别? JDK:Java Development Kit 的简称,java 开发工具包,提供了 java 的开发环境和运行环境. JRE:Java Runtime Env ...
- jq的ajax方法
相较与js异步对象的繁琐,jq的ajax对象结构更加清晰 一:ajax对象简述 ajax(Asynchronous JavaScript and XML),异步的xml和js对象,主要用于在不刷新全局 ...
