【XSY3306】alpha - 线段树+分治NTT

题目来源：noi2019模拟测试赛（一）

题意：

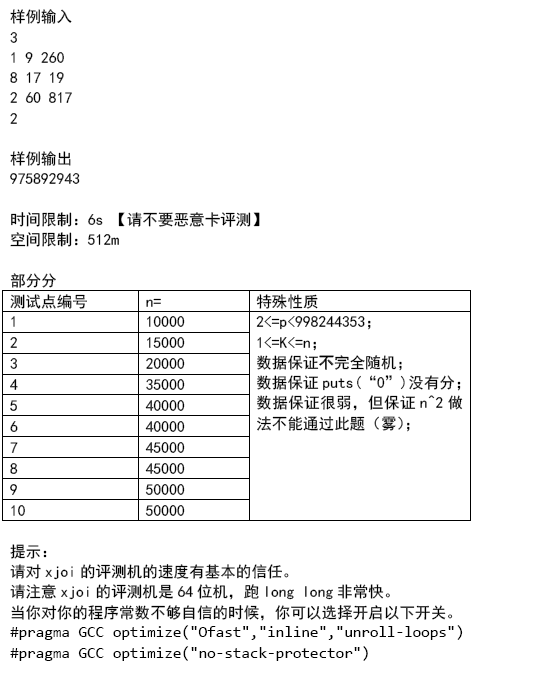
题解：

这场三道神仙概率期望题……orzzzy

这题暴力$O(n^2)$有30分，但貌似比正解更难想……（其实正解挺好想的）

注意到一次操作实际上就是在一段区间里乘上了一个形如$px+(1-p)$的多项式，设把所有多项式合并得到一个多项式$F(x)$，那么我们要求的答案实际上就是：

$$[x^k]F(x)$$

那么可以先离散化坐标，然后开一棵线段树，用vector维护每个点（即最小不可再分的区间）上要乘的多项式，最后dfs一遍线段树，用分治NTT合并每个点自身的多项式，再合并子树的多项式即可。

时间复杂度$O(nlog^3n)$

口胡起来很简单但是写起来很恶心……

代码：

NTT写的挫，人傻自带大常数，跑了4.3s

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<cmath>
 #include<queue>
 #define inf 2147483647
 #define eps 1e-9
 #define mod 998244353
 #define G 3
 using namespace std;
 typedef long long ll;
 typedef double db;
 struct task{
     int l,r,p;
 }t[];
 struct node{
     int l,r;
 }tr[];
 int n,k,cnt=,tn=,nw[],tmp[],lsh[],ans[][];
 vector<int>v[];
 namespace Poly{
     namespace NTT{
         int bit,bitnum,rev[],W[][];
         int fastpow(int x,int y){
             int ret=;
             for(;y;y>>=,x=(ll)x*x%mod){
                 if(y&)ret=(ll)ret*x%mod;
             }
             return ret;
         }
         void pre(){
             int rG=fastpow(G,mod-);
             for(int i=;i<=;i++){
                 W[<<i][]=fastpow(G,(mod-)/(<<i));
                 W[<<i][]=fastpow(rG,(mod-)/(<<i));
             }
         }
         void getr(int l){
             for(bit=,bitnum=;bit<l;bit<<=,bitnum++);
             for(int i=;i<bit;i++){
                 rev[i]=(rev[i>>]>>)|((i&)<<(bitnum-));
             }
         }
         void ntt(int *s,int op){
             for(int i=;i<bit;i++){
                 if(i<rev[i])swap(s[i],s[rev[i]]);
             }
             for(int i=;i<bit;i<<=){
                 int w=W[i<<][op==-];
                 for(int p=i<<,j=;j<bit;j+=p){
                     int wk=;
                     for(int k=j;k<i+j;k++,wk=(ll)wk*w%mod){
                         int x=s[k],y=(ll)s[k+i]*wk%mod;
                         s[k]=(x+y)%mod;
                         s[k+i]=(x-y+mod)%mod;
                     }
                 }
             }
             if(op==-){
                 int rb=fastpow(bit,mod-);
                 for(int i=;i<bit;i++){
                     s[i]=(ll)s[i]*rb%mod;
                 }
             }
         }
     }
     int A[],B[];
     void getmul(int *s,int *a,int *b,int len1,int len2){
         for(int i=;i<=len1;i++)A[i]=a[i];
         for(int i=;i<=len2;i++)B[i]=b[i];
         NTT::getr((len1+len2)*);
         for(int i=len1+;i<NTT::bit;i++)A[i]=;
         for(int i=len2+;i<NTT::bit;i++)B[i]=;
         NTT::ntt(A,);
         NTT::ntt(B,);
         for(int i=;i<NTT::bit;i++){
             s[i]=(ll)A[i]*B[i]%mod;
         }
         NTT::ntt(s,-);
     }
     void mul(int l,int r,int nw,int *s){
         if(l==r){
             s[]=(mod-v[nw][l]+);
             s[]=v[nw][l];
             return;
         }
         int mid=(l+r)/;
         mul(l,mid,nw,s);
         mul(mid+,r,nw,s+mid-l+);
         getmul(s,s,s+mid-l+,mid-l+,r-mid);
     }
 }
 void updata(int l,int r,int u,int L,int R,int p){
     if(L<=tr[l].l&&tr[r].r<=R){
         v[u].push_back(p);
         return;
     }
     int mid=(l+r)/;
     if(L<=tr[mid].r)updata(l,mid,u*,L,R,p);
     if(tr[mid+].l<=R)updata(mid+,r,u*+,L,R,p);
 }
 int dfs(int l,int r,int u,int x){
     int mid=(l+r)/,L,R,mx;
     if(l<r){
         L=dfs(l,mid,u*,x);
         R=dfs(mid+,r,u*+,x+);
         mx=max(L,R);
     }
     if(v[u].size()){
         Poly::mul(,v[u].size()-,u,tmp);
     }else tmp[]=;
     if(l==r){
         nw[]=(tr[l].r-tr[l].l+);
         Poly::getmul(ans[x],nw,tmp,,v[u].size());
         return v[u].size();
     }
     for(int i=L+;i<=mx;i++)ans[x][i]=;
     for(int i=R+;i<=mx;i++)ans[x+][i]=;
     for(int i=;i<=mx;i++){
         ans[x][i]=(ans[x][i]+ans[x+][i])%mod;
     }
     Poly::getmul(ans[x],ans[x],tmp,mx,v[u].size());
     return v[u].size()+mx;
 }
 int main(){
     scanf("%d",&n);
     Poly::NTT::pre();
     for(int i=;i<=n;i++){
         scanf("%d%d%d",&t[i].l,&t[i].r,&t[i].p);
         lsh[++cnt]=t[i].l;
         lsh[++cnt]=t[i].r+;
     }
     scanf("%d",&k);
     lsh[++cnt]=;
     lsh[++cnt]=;
     sort(lsh+,lsh+cnt+);
     cnt=unique(lsh+,lsh+cnt+)-lsh-;
     for(int i=;i<=cnt;i++){
         tr[++tn].l=lsh[i-];
         tr[tn].r=lsh[i]-;
     }
     for(int i=;i<=n;i++){
         updata(,tn,,t[i].l,t[i].r,t[i].p);
     }
     dfs(,tn,,);
     printf("%d",ans[][k]);
     return ;
 }