js确认框confirm()用法实例详解
先为大家介绍javascript确认框的三种使用方法,具体内容如下
第一种方法:挺好用的,确认以后才能打开下载地址页面。原理也比较清晰。主要用于删除单条信息确认。
|
1
2
3
4
5
6
7
8
9
10
|
<SCRIPT LANGUAGE=javascript> function del() { var msg = "您真的确定要删除吗?\n\n请确认!"; if (confirm(msg)==true){ return true; }else{ return false; } } </SCRIPT> |
调用方法:
|
1
|
<a href="del.php?id=123" onclick="javascript:return del()">删 除</a> |
第二种方法:原理跟上面的一样。JavaScript删除确认框
|
1
|
<a href="javascript:if(confirm('确实要删除吗?'))location='jb51.php?id='">删除</a> |
第三种方法:主要用于批量删除的确认提示
|
1
2
3
4
5
6
7
8
9
10
11
|
<input name="Submit" type="submit" class="inputedit" value="删除" onclick="{if(confirm('确定纪录吗?')){ this.document.formname.submit(); return true;}return false; }"> <input name="按钮" type="button" ID="ok" onclick="{if(confirm('确定删除吗?')){ window.location='Action.asp?Action=Del& TableName=Item& ID=<%=ID%>'; return true;}return false;}" value="删除栏目" /> |
再为大家分享一个实例:js的确认框confirm()代码实例
效果图:
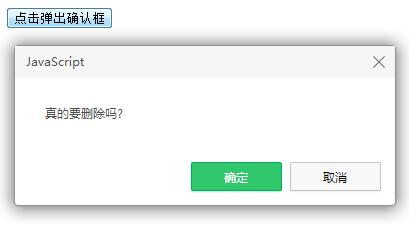
confirm()确认框在网页中比较常用,当然有些美观度要求比较高的网页可能需要自定义这样的功能,下面就来介绍一下window对象的confirm()函数的用法,下面县看一段代码实例,因为没有什么再比这个更直观了。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
<!DOCTYPE html> <html> <head> <meta charset="gb2312"> <title>confirm()代码实例</title> <script type="text/javascript"> window.onload=function(){ var bt=document.getElementById("bt"); bt.onclick=function(){ if(confirm("真的要删除吗?")){ alert("点击了确认按钮"); } else{ alert("点击了取消按钮"); } }}</script> </head> <body> <input type="button" id="bt" value="点击弹出确认框" /></body> </html> |
以上代码是一个confirm的简单实例,可以很清晰的演示confirm()的作用,下面做一些总结:
1.confirm()函数中的参数是确认框的提示语。
2.此函数返回值是布尔型的,点击确定,返回值为true,点击取消返回值为false。
以上就是关于js确认框confirm()用法的实例,内容很丰富,希望大家喜欢。
js确认框confirm()用法实例详解的更多相关文章
- python中argparse模块用法实例详解
python中argparse模块用法实例详解 这篇文章主要介绍了python中argparse模块用法,以实例形式较为详细的分析了argparse模块解析命令行参数的使用技巧,需要的朋友可以参考下 ...
- JS JSOP跨域请求实例详解
JSONP(JSON with Padding)是JSON的一种“使用模式”,可用于解决主流浏览器的跨域数据访问的问题.这篇文章主要介绍了JS JSOP跨域请求实例详解的相关资料,需要的朋友可以参考下 ...
- 【python库模块】Python subprocess模块功能与常见用法实例详解
前言 这篇文章主要介绍了Python subprocess模块功能与常见用法,结合实例形式详细分析了subprocess模块功能.常用函数相关使用技巧. 参考 1. Python subprocess ...
- PHP中__get()和__set()的用法实例详解
php面向对象_get(),_set()的用法 一般来说,总是把类的属性定义为private,这更符合现实的逻辑.但是,对属性的读取和赋值操作是非常频繁的,因此在PHP5中,预定义了两个函数“__ge ...
- jQuery中on()方法用法实例详解
这篇文章主要介绍了jQuery中on()方法用法,实例分析了on()方法的功能及各种常见的使用技巧,并对比分析了与bind(),live(),delegate()等方法的区别,需要的朋友可以参考下 本 ...
- js事件监听器用法实例详解
这篇文章主要介绍了js事件监听器用法,以实例形式较为详细的分析了javascript事件监听器使用注意事项与相关技巧,需要的朋友可以参考下本文实例讲述了js事件监听器用法.分享给大家供大家参考.具体分 ...
- js事件监听器用法实例详解-注册与注销监听封装
本文实例讲述了js事件监听器用法.分享给大家供大家参考.具体分析如下: 1.当同一个对象使用.onclick的写法触发多个方法的时候,后一个方法会把前一个方法覆盖掉,也就是说,在对象的onclick事 ...
- jquery中attr()与prop()函数用法实例详解(附用法区别)
本文实例讲述了jQuery中attr()与prop()函数用法.分享给大家供大家参考,具体如下: 一.jQuery的attr()方法 jquery中用attr()方法来获取和设置元素属性,attr是a ...
- Python回调函数用法实例详解
本文实例讲述了Python回调函数用法.分享给大家供大家参考.具体分析如下: 一.百度百科上对回调函数的解释: 回调函数就是一个通过函数指针调用的函数.如果你把函数的指针(地址)作为参数传递给另一个函 ...
随机推荐
- [雅礼NOIP2018集训 day3]
考试的时候刚了T1两个小时线段树写了三个子任务结果发现看错了题目,于是接下来一个半小时我自闭了 result=历史新低 这告诉我们,打暴力要端正态度,尤其是在发现自己之前出锅的情况下要保持心态的平和, ...
- Django(part2)
admin site:django自带了admin site,我们需要创建能访问site的用户 #以交互的方式创建超级用户 manage.py createsuperuser 如果要把model加到a ...
- (转载) android快速搭建项目积累
android快速搭建项目积累 2016-04-05 20:07 519人阅读 评论(0) 收藏 举报 分类: android优化(8) Rx技术(5) 版权声明:本文为博主原创文章,未经博主 ...
- 接口测试工具篇--jmeter
jmeter的安装及使用在这里不进行讲解了,网上有很多资料 下面开始讲解如何使用jmeter做http接口测试 在jmeter中添加一个http请求,添加方式:测试计划上邮件添加线程组,线程组上邮件选 ...
- Uncaught TypeError: Cannot read property 'offsetTop' of undefined at VueComponent.handleScroll
mounted() { window.addEventListener("scroll", this.handleScroll); }, beforeDestroy() { win ...
- How Javascript works (Javascript工作原理) (二) 引擎,运行时,如何在 V8 引擎中书写最优代码的 5 条小技巧
个人总结: 一个Javascript引擎由一个标准解释程序,或者即时编译器来实现. 解释器(Interpreter): 解释一行,执行一行. 编译器(Compiler): 全部编译成机器码,统一执行. ...
- 【BZOJ4383】[POI2015]pustynia
题意: 建议Alt+F4百度一下 题解: 差分约束+线段树优化建图,直接按照拓扑序跑就行了 代码: #include<iostream> #include<cstring> # ...
- myssql数据库表名转驼峰 - PLAY - ITeye博客
原文:myssql数据库表名转驼峰 - PLAY - ITeye博客
- Java基础学习总结(46)——JAVA注解快速入门
各位开发童鞋,注解这个东西我们肯定每天都能看见,也许有时候看的太多了到是会忽略注解这东西具体是如何工作的.今天在这里用最短的篇幅快速讲解下注解的原理,对这块记的不太清楚的同学也可以再次看看,下次有人详 ...
- [terry笔记]11gR2_dataguard_主备库切换
主备库切换 Switchover 一般SWITCHOVER切换都是计划中的切换,特点是在切换后,不会丢失任何的数据,而且这个过程是可逆的,整个DATA GUARD环境不会被破坏,原来DATA GU ...
