php实现记忆化递归--以斐波那契数列为例（还是以边学边做为主，注重练习）

php实现记忆化递归--以斐波那契数列为例（还是以边学边做为主，注重练习）

一、总结

1、递归不优化的话，30层开外就有点吃力了

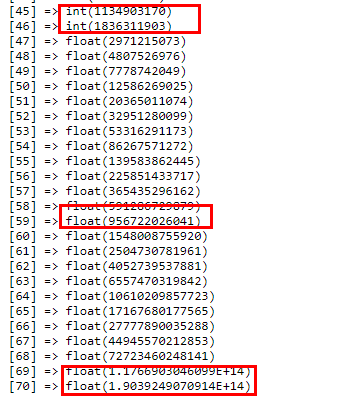
2、php因为定义变量的时候不用定义变量类型，所以数组里面的类型也是php自动选择，这就会有下面的情况：

当int不够的时候自动转化为float，float不够的时候自动转化为科学计数法

二、php实现记忆化递归--以斐波那契数列为例

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。

三、代码

代码一

 <?php

 $arr = array(0,1,1);
 for($i=3;$i<=100;$i++){$arr[$i]=-1;}
 function Fibonacci($n)
 {
     global $arr;
     if($arr[$n]!=-1) return $arr[$n]; //1、边界情况都可以结合 记忆化递归数组判断，对比一下下面的代码就知道简便之处了
     else{
         $arr[$n-1]=$arr[$n-1]!=-1?$arr[$n-1]:Fibonacci($n-1);
         $arr[$n-2]=$arr[$n-2]!=-1?$arr[$n-2]:Fibonacci($n-2);
         return $arr[$n]=$arr[$n-1]+$arr[$n-2];
     }
 }

代码二

 <?php
 namespace app\index\controller;

 use app\index\controller\Base;

 class Exercise extends Base
 {
     public function index()
     {
         $this->FibonacciDemo();
     }

     //斐波那契数列
     private $arr = array();//记忆化递归数组
     public function Fibonacci($n)
     {
         global $arr;
         if($n==0) return 0;
         else if($n==1||$n==2) return 1; //1、php中的逻辑连接符：和java一样,例如|表示位运算符，||表示逻辑运算符
         else{
             $arr[$n-1]=$arr[$n-1]!=-1?$arr[$n-1]:$this->Fibonacci($n-1);
             $arr[$n-2]=$arr[$n-2]!=-1?$arr[$n-2]:$this->Fibonacci($n-2);
             return $arr[$n]=$arr[$n-1]+$arr[$n-2]; //2、支持这样的返回方式，这应该是先赋值再返回  3、把求出的值给记录下数组，刚刚忘记记录$arr[$n]了
         }
     }
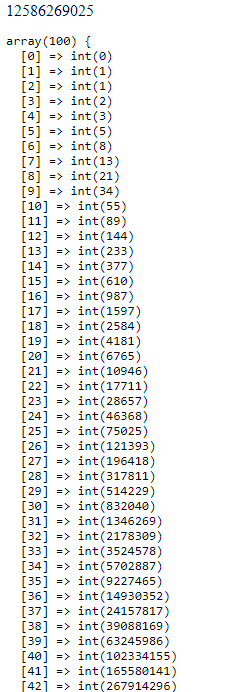
     public function FibonacciDemo(){
         global $arr;
         for ($i=0; $i <100 ; $i++) {
             $arr[$i]=-1;
         }
         $arr[0]=0;
         $arr[1]=1;
         $arr[2]=1;
         echo($this->Fibonacci(50));
         dump($arr);die;
     }

 }

截图：