NOIP模拟赛-旅行者问题 解题报告

旅行者问题

【问题描述】

lahub是一个旅行者的粉丝，他想成为一个真正的旅行者，所以他计划开始一段旅行。lahub想去参观n个目的地（都在一条直道上）。lahub在起点开始他的旅行。第i个目的地和起点的距离为ai千米（ai为非负整数）。不存在两个目的地和起点的距离相同。

从第i个目的地走到第j个目的地所走的路程为 |ai-aj|千米。我们把参观n个目的地的顺序称作一次“旅行”。lahub可以参观他想要参观的任意顺序，但是每个目的地有且只能被参观一次（参观顺序为n的排列）。

lahub把所有可能的“旅行”都写在一张纸上，并且记下每个“旅行”所要走的路程。他对所有“旅行”的路程之和的平均值感兴趣。但是他觉得计算太枯燥了，所以就向你寻求帮助。

【输入格式】

第一行一个正整数n。

第二行n个非负整数a1,a2,....,an（1≤ai≤10^7）。

【输出格式】

两个整数，答案用最简分数形式输出，第一个为分子，第二个为分母。

【输入样例】

3

2 3 5

【输出样例】

22 3

【样例提示】

样例有6种可能的旅行：

[2, 3, 5]: 该“旅行”的路程：|2 – 0| + |3 – 2| + |5 – 3| = 5;

[2, 5, 3]: |2 – 0| + |5 – 2| + |3 – 5| = 7;

[3, 2, 5]: |3 – 0| + |2 – 3| + |5 – 2| = 7;

[3, 5, 2]: |3 – 0| + |5 – 3| + |2 – 5| = 8;

[5, 2, 3]: |5 – 0| + |2 – 5| + |3 – 2| = 9;

[5, 3, 2]: |5 – 0| + |3 – 5| + |2 – 3| = 8.

答案为 1/6 * （5+7+7+8+9+8）=44/6=22/3

【数据范围】

30% n<=10

50% n<=1000

100% n<=100000

分析：

这道题的不免会让人想起用DFS搜下去。打出来个全排列出来。为了全排列可能还用预处理两点之间的位置。不过。做这些事情。恩。还是给WA了。

而这道题再进一步思考呢？会让人想到。如果，只是对每条边进行一个处理呢？思考--->每条边(两个点之间的距离)对最终的答案的影响。那么如果我们走了这条边，我们接下来会有多少种路可以走呢，也就是接下来有多少种组合呢? 假设我们选择了Ai 与 Aj 这条路，接下来就会有(n-2)！种方案。那么Ai与Aj这条路就会走(n-2)!次。而这条路又有(n-1)种选择。因为我们可以选择在什么时候再走。这个时候方案数就又多了。是 (n-2)!*(n-1) ==(n-1)！。但是我们光枚举了两点之间的距离，没有枚举从起点开始的路径。而从头开始的路径的位置是固定的。假设我们从0到Ai。那么走完之后就有(n-1)!种方案。/-乘法原理-/。这样每次的情况又枚举完了。乘上权值就是我们最后的总和。

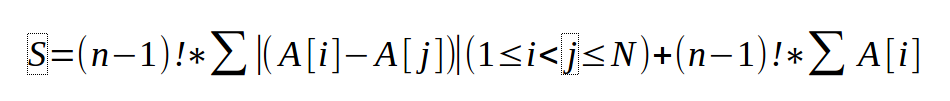
最关键的就是我们如何去枚举整个sum(abs(A[i]-A[j])；首先，我们可以确定的是。我们就只用计算从i到j 并且 (i>j)这样计算，总路程就×2就好（走过去，走回来）。

我们可以用递推来实现整个计算。我们可以发现一个规律：

假设a1 > a2 > a3 > a4，

以Ai为结尾的Ai-Aj的和为Si，

那么：

S2 = a1 - a2

S3 = a1 - a3 + a2 - a3 = (a1 - a2 + a2 - a3) + a2 - a3 = S2 + 2 *（a2 - a3）

S4 = a1 - a4 + a2 - a4 + a3 - a4 = (a1 - a3 + a3 - a4) + (a2 - a3 + a3 - a4) + (a3 - a4)

= S3 + 3 * (a3 - a4)

我们发现这里的S是可以递推的。

最后在计算结果的时候 分子是总和。而分母是总方案数n! 分数相约之后。分母就只剩一个n。那么我们就只需要计算gcd再同时除以gcd。

放出代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int line[1000001];
int n;
long long int gcd(long long int a,long long int b)
{
    return a%b==0 ? b : gcd(b,a%b);
}
int cmp(int a,int b)
{
    return a>b;
}
int main()
{
    freopen("tourist.in","r",stdin);
    freopen("tourist.out","w",stdout);
    long long int sum=0;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
    scanf("%d",&line[i]);
    sum+=line[i];
    }
    sort(line+1,line+1+n,cmp);
    long long int k=0,ans=0;
    for(int i=2;i<=n;++i)
    {
    k=k+(i-1)*(line[i-1]-line[i]);
    ans+=k;
    }
    sum+=ans*2;
    long long int c=gcd(sum,n);
    printf("%I64d %I64d",sum/c,n/c);
    fclose(stdin);
    fclose(stdout);
    return 0;
}