感知机的对偶形式——python3实现

　　运用对偶的（对应原始）感知机算法实现线性分类。

　　参考书目：《统计学习方法》(李航)

　　算法原理：

　　代码实现：

　　环境：win7 32bit + Anaconda3 +spyder

　　和原始算法的实现基本框架是类似的，只是判断和权值的更新算法有点变化。

 # -*- coding: utf-8 -*-
 """
 Created on Fri Nov 18 01:29:35 2016

 @author: Administrator
 """

 import numpy as np
 from matplotlib import pyplot as plt

 # train matrix
 def get_train_data():
     M1 = np.random.random((100,2))
     # 将label加到最后，方便后面操作
     M11 = np.column_stack((M1,np.ones(100)))

     M2 = np.random.random((100,2)) - 0.7
     M22 = np.column_stack((M2,np.ones(100)*(-1)))
     # 合并两类，并将位置索引加到最后
     MA = np.vstack((M11,M22))
     MA = np.column_stack((MA,range(0,200)))

     # 作图操作
     plt.plot(M1[:,0],M1[:,1], 'ro')
     plt.plot(M2[:,0],M2[:,1], 'go')
     # 为了美观，根据数据点限制之后分类线的范围
     min_x = np.min(M2)
     max_x = np.max(M1)
     # 分隔x,方便作图
     x = np.linspace(min_x, max_x, 100)
     # 此处返回 x 是为了之后作图方便
     return MA,x

 # GRAM计算
 def get_gram(MA):
     GRAM = np.empty(shape=(200,200))
     for i in range(len(MA)):
         for j in range(len(MA)):
             GRAM[i,j] = np.dot(MA[i,][:2], MA[j,][:2])
     return GRAM

 # 方便在train函数中识别误分类点
 def func(alpha,b,xi,yi,yN,index,GRAM):
     pa1 = alpha*yN
     pa2 = GRAM[:,index]
     num = yi*(np.dot(pa1,pa2)+b)
     return num

 # 训练training data
 def train(MA, alpha, b, GRAM, yN):
     # M 存储每次处理后依旧处于误分类的原始数据
     M = []
     for sample in MA:
         xi = sample[0:2]
         yi = sample[-2]
         index = int(sample[-1])
         # 如果为误分类，改变alpha,b
         # n 为学习率
         if func(alpha,b,xi,yi,yN,index,GRAM) <= 0:
             alpha[index] += n
             b += n*yi
             M.append(sample)
     if len(M) > 0:
         # print('迭代...')
         train(M,  alpha, b, GRAM, yN)
     return alpha,b

 # 作出分类线的图
 def plot_classify(w,b,x, rate0):
     y = (w[0]*x+b)/((-1)*w[1])
     plt.plot(x,y)
     plt.title('Accuracy = '+str(rate0))

 # 随机生成testing data 并作图
 def get_test_data():
     M = np.random.random((50,2))
     plt.plot(M[:,0],M[:,1],'*y')
     return M
 # 对传入的testing data 的单个样本进行分类
 def classify(w,b,test_i):
     if np.sign(np.dot(w,test_i)+b) == 1:
         return 1
     else:
         return 0

 # 测试数据，返回正确率
 def test(w,b,test_data):
     right_count = 0
     for test_i in test_data:
         classx = classify(w,b,test_i)
         if classx == 1:
             right_count += 1
     rate  = right_count/len(test_data)
     return rate

 if __name__=="__main__":
     MA,x= get_train_data()
     test_data = get_test_data()
     GRAM = get_gram(MA)
     yN = MA[:,2]
     xN = MA[:,0:2]
     # 定义初始值
     alpha = [0]*200
     b = 0
     n = 1
     # 初始化最优的正确率
     rate0 = 0

 #    print(alpha,b)
 #    循环不同的学习率n,寻求最优的学习率，即最终的rate0
 #    w0,b0为对应的最优参数
     for i in np.linspace(0.01,1,100):
         n = i
         alpha,b = train(MA, alpha, b, GRAM, yN)
         alphap = np.column_stack((alpha*yN,alpha*yN))
         w = sum(alphap*xN)
         rate = test(w,b,test_data)
         # print(w,b)
         rate = test(w,b,test_data)
         if rate > rate0:
             rate0 = rate
             w0 = w
             b0 = b
             print('Until now, the best result of the accuracy on test data is '+str(rate))
             print('with w='+str(w0)+' b='+str(b0))
             print('---------------------------------------------')
 #     在选定最优的学习率后，作图
     plot_classify(w0,b0,x,rate0)
     plt.show()

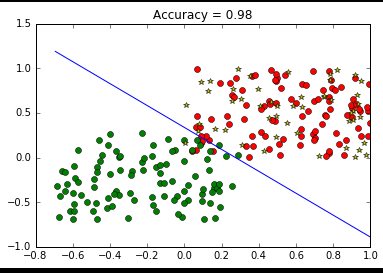
　　输出：