运输问题的+Leapms模型

运输问题的+Leapms模型

运输问题是本科教课书中的一个经典章节。运输问题的线性规划模型非常简单，而且求解难度极小。

问题

一个公司生产并销售一种产品。该公司有m个产地、n个销地。产地 i 的供给量不大于p[i]，销地 j 的需求量不小于d[i]，从 i 到 j 的运输费用为 c[i][j]。要求规划产地到销地之间的调运量，使得调用总费用最小。

数据

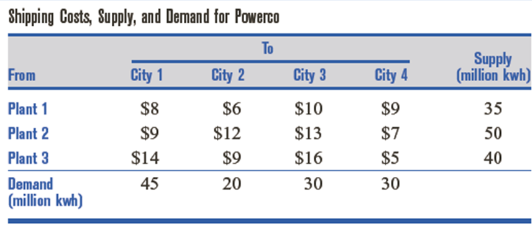
以下是教课书[1，2]中的一个运输问题的数据表：

+Leapms模型语言常识

1、sub-index： 在大多数计算机语言中，如c语言、python语言中，用[ ]表示脚标， [ ] 被读作 sub-index （脚标）。例如x[i][j] 就相当于$x_{ij}$, 被读成 x sub-index i,j 。+Leapms建模语言也不例外。

2、of: 在大多数计算机语言中， () 一般有两个用途—— （1） 表示算式的优先等级、（2）表示函数，例如sin(a)；当 ( )表示函数时，读做of, 例如sina(a)读做 sine of a。+Leapms使用这种习惯。

3、花括号{ } : +Leapms中的花括号有两个用法，（1）表示数据区里的数据集合、（2）表示累加或累乘中局部变量的变化范围。 例如 $\sum_{i=1}^m\sum_{i=1}^nx_{ij}c_{ij}$在+Leapm中就被写成 sum{i=1,...,m; j=1,...,n} x[i][j]c[i][j]。

4、注释：+Leapms的注释符号是//，从//开始到行结束都被当作注释忽略

运输问题的建模

设x[i][j]为从产地 i 到销地 j 的调运量，则调运总费用是 sum{i=1,...,m;j=1,...,n} x[i][j]c[i][j]，于是模型的目标为

minimize sum{i=1,..,m;j=1,..,n}c[i][j]x[i][j]   //（1）

产量约束

sum{j=1,...,n}x[i][j] <= s[i] | i=1,...,m //（2）

销量约束
      sum{i=1,...,m}x[i][j] >= d[j] | j=1,...,n //（3）

于是运输问题模型的主要部分即：

minimize sum{i=1,..,m;j=1,..,n}c[i][j]x[i][j]   //（1）
subject to
    sum{j=1,...,n}x[i][j] <= s[i] | i=1,...,m   //（2）
    sum{i=1,...,m}x[i][j] >= d[j] | j=1,...,n   //（3）

+Leapms要求对所有出现在模型中的符号进行说明：

where
    m,n are integers
    c[i][j] is a number|i=1,...,m;j=1,...,n
    d,s are sets
    x[i][j] is a variable of nonnegative number|-->
               i=1,...,m;j=1,...,n

为了使得模型能够被解析和求解，必须给出数据：

data
    m=3
    n=4
    c={
        8  6 10 9
        9 12 13 7
       14  9 16 5
    }
    d={45 20 30 30}
    s={35 50 40}

模型的解析和求解

+Leapms模型使用纯文本表达。

在+Leapms环境中用Load命令即可调入模型并对模型进行解析。解析完毕后会报告模型的变量数和约束数。

然后使用solve命令求解。（如果有整形或者0-1变量，则需使用mip命令求解，否则只进行松弛求解）。

cplex命令或gurobi命令可以调用cplex或gurobi软件对模型进行求解。

+Leapms>load
 Current directory is "ROOT".
 .........
        transportation.leap
 .........
please input the filename:transportation
================================================================
1:  minimize sum{i=1,..,m;j=1,..,n}c[i][j]x[i][j]   //（1）
2:  subject to
3:      sum{j=1,...,n}x[i][j] <= s[i] | i=1,...,m   //（2）
4:      sum{i=1,...,m}x[i][j] >= d[j] | j=1,...,n   //（3）
5:  where
6:      m,n are integers
7:      c[i][j] is a number|i=1,...,m;j=1,...,n
8:      d,s are sets
9:      x[i][j] is a variable of nonnegative number|-->
10:                 i=1,...,m;j=1,...,n
11:  data
12:      m=3
13:      n=4
14:      c={
15:          8  6 10 9
16:          9 12 13 7
17:         14  9 16 5
18:      }
19:      d={45 20 30 30}
20:      s={35 50 40}
21:
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=12
number of constraints=7
..................................
+Leapms>solve
The LP is solved to optimal.
找到线性规划最优解.非零变量值和最优目标值如下：
    .........
    x1_2*=10
    x1_3*=25
    x2_1*=45
    x2_3*=5
    x3_2*=10
    x3_4*=30
    .........
    Objective*=1020
    .........
+Leapms>

上面的求解结果给出非零最优决策变量和最优目标值。该题最优目标值为1020。

上面的运输模型求解难度很小，商用求解器可以在一个小时甚至更短时间内内求解到百万级变量的问题。

LaTex 模型的自动生成

在+Leapms环境中使用命令“Latex” 会自动生成 LaTex文件(.tex)，在安装有LaTex环境的系统中双击此文件能够自动生成数学形式的pdf模型。

\documentclass{article}
\usepackage{amsmath}\begin{document}
\section{LaTex code for Model ``Transportation.leap"}

\rule[0pt]{5cm}{0.05em}\\
\begin{align}
\min\quad \sum_{i=1}^{m}\sum_{j=1}^{n}c_{ij}x_{ij}\end{align}
subject to
\begin{align}
&\sum_{j=1}^{n}x_{ij}\leq s_{i},\quad i=1,...,m\\
&\sum_{i=1}^{m}x_{ij}\geq d_{j},\quad j=1,...,n\\&x_{ij}\geq 0 , \quad i=1\ldots m; j=1\ldots n
\end{align}
\\\rule[0pt]{5cm}{0.05em}\\
The above formulations are generated by +Leapms from model file ``Transportation.leap" at 11:34:24 2018-12-27.
\end{document}

由上面自动生成的LaTex代码所进一步生成的pdf数学模型：

参考文献

[1] Wayne L. Winston. Operations Research: Applications and Algorithms. Duxbury press, boston, 1997

[2] Wayne L. Winston. 运筹学(数学规划 第3版 影印版). 北京：清华大学出版社，2004