机器学习基石：14 Regularization

一、正则化的假设集合

通过从高次多项式的H退回到低次多项式的H来降低模型复杂度,

以降低过拟合的可能性,

如何退回?

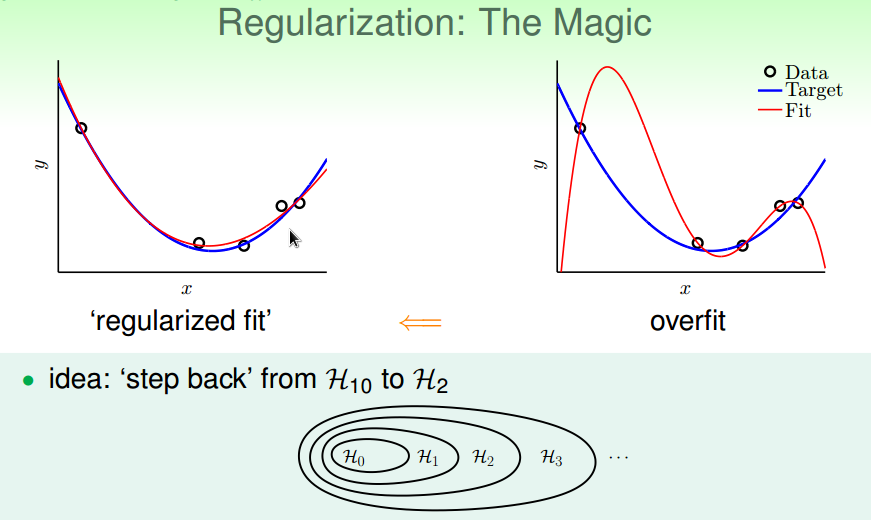
通过加约束条件：

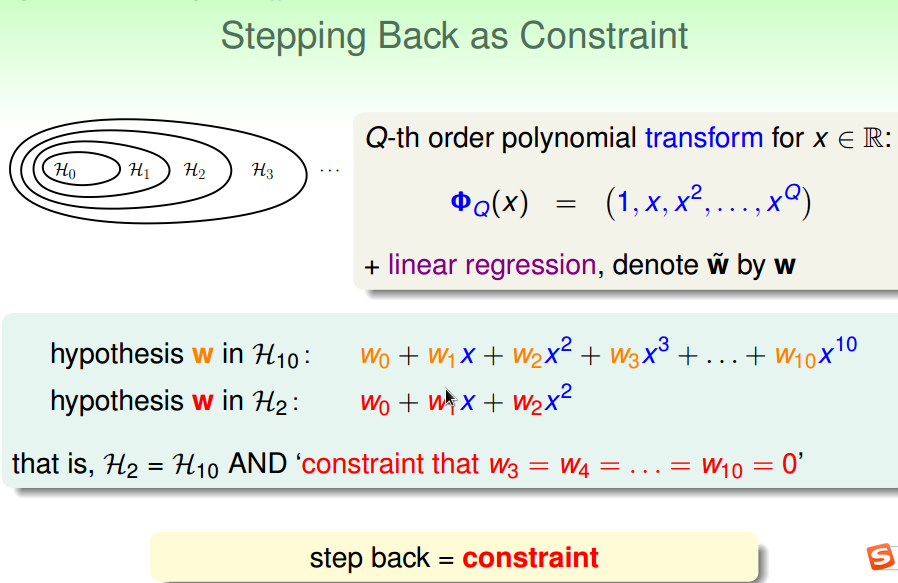
如果加了严格的约束条件,

没有必要从H₁₀退回到H₂,

直接使用H₂就可以了。

加上松弛点的约束条件,

使得模型比H₂复杂,

但到不了H₁₀那么复杂。

二、权重衰减正则化

通过拉格朗日乘子法处理带约束的优化问题,

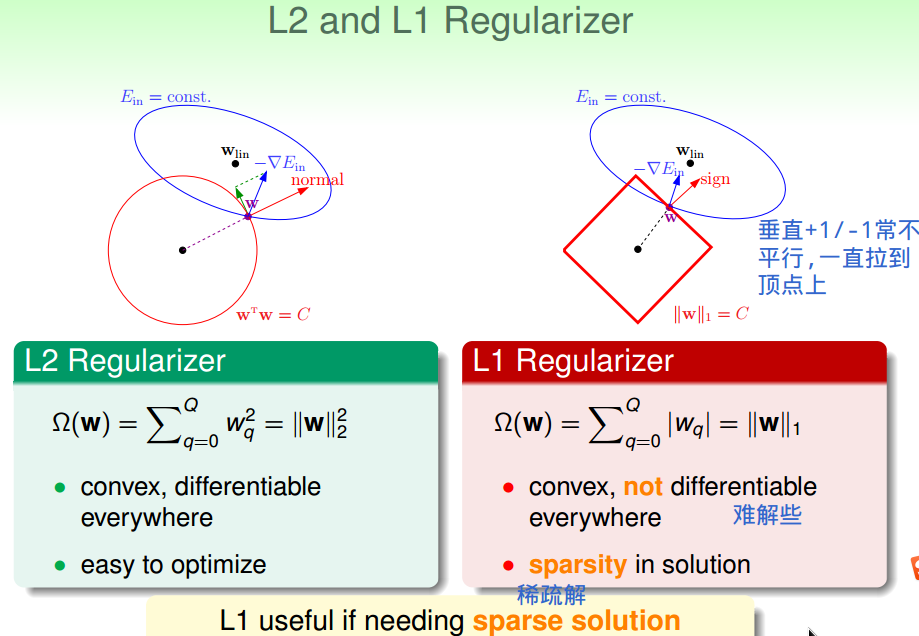
只看谷的话,需沿着梯度反方向下降到谷底;

只看超球面的话,需沿着垂直于法向量的方向滚;

判断当前W是否是最优解就看它能否在超球面上的同时还能向更接近谷底的方向滚,

数学上,可理解为梯度反方向在法向量方向上投影不为0,

否则,即梯度反方向平行于当前法向量,此时已经是最优解。

------可视化解释。

也可以通过求导证到相同结论。

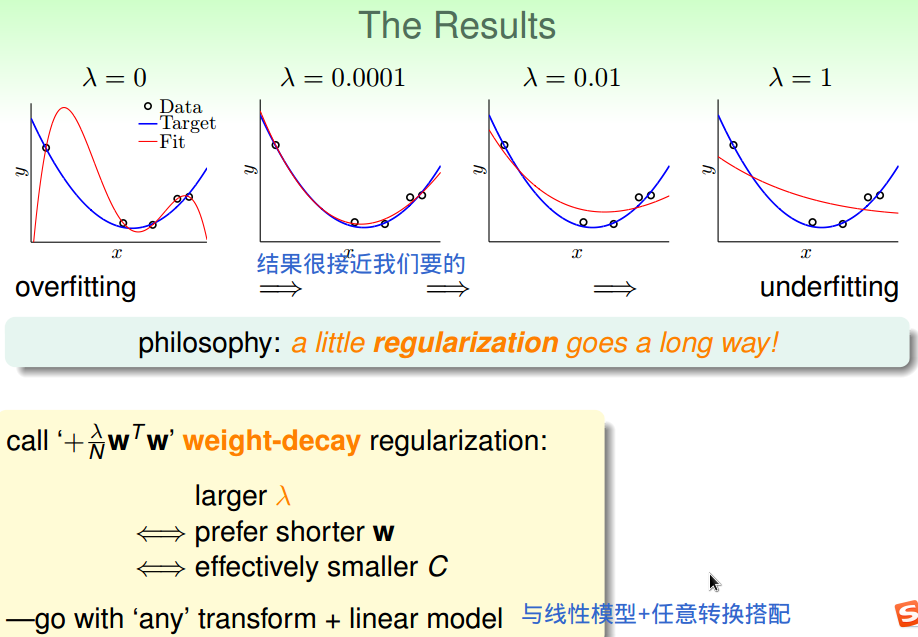
权重衰减正则项------权重大小受到限制。

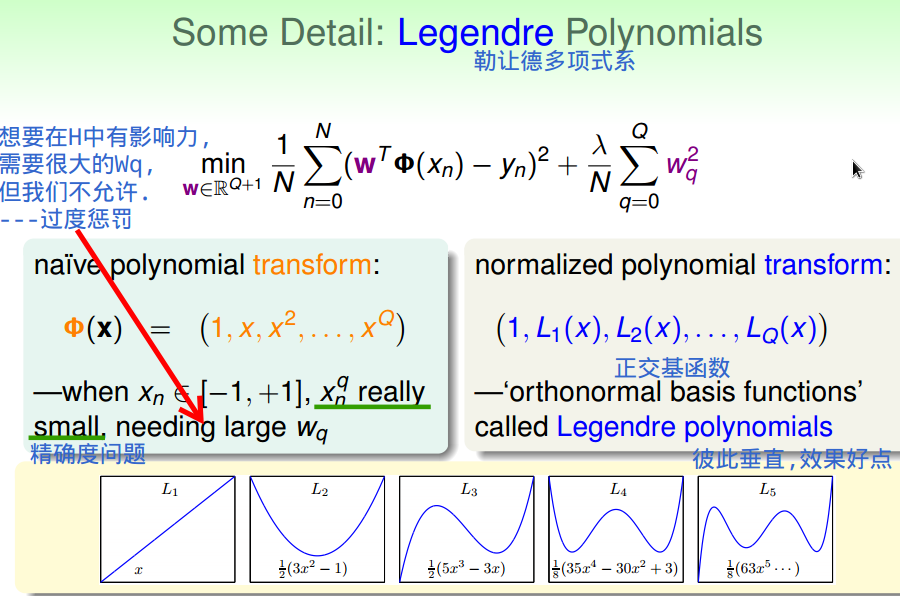
三、正则化和VC理论

正则化后,

有效VC维变小。

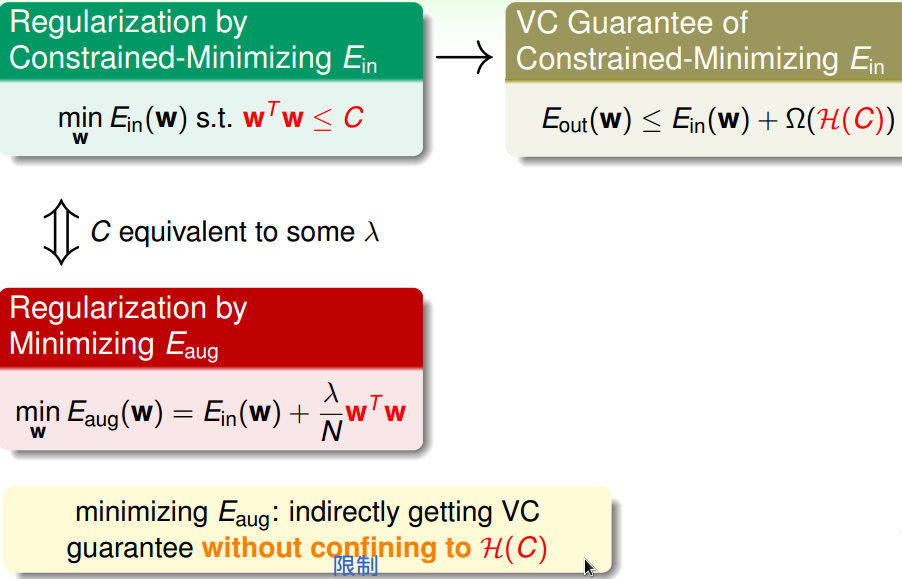
四、通用正则项

通用正则项选择:

基于目标的,情理上说得通的,便于求解的。

与代价函数选择类似。

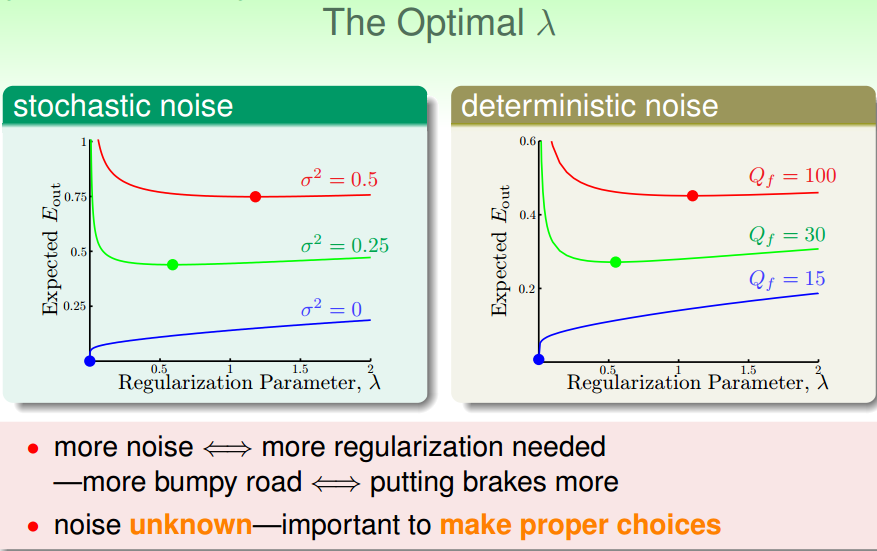
注:

namuta=lambda.