【自适应辛普森积分】hdu1724 Ellipse

Ellipse

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2502    Accepted Submission(s): 1126

Problem Description

Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..
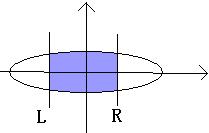
Look this sample picture:

A
ellipses in the plane and center in point O. the L,R lines will be
vertical through the X-axis. The problem is calculating the blue
intersection area. But calculating the intersection area is dull, so I
have turn to you, a talent of programmer. Your task is tell me the
result of calculations.(defined PI=3.14159265 , The area of an ellipse
A=PI*a*b )

 

Input

Input
may contain multiple test cases. The first line is a positive integer
N, denoting the number of test cases below. One case One line. The line
will consist of a pair of integers a and b, denoting the ellipse
equation 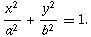, A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).

 

Output

For
each case, output one line containing a float, the area of the
intersection, accurate to three decimals after the decimal point.

 

Sample Input

2

2 1 -2 2

2 1 0 2

 

Sample Output

6.283

3.142

 

Author

威士忌

题意

给定椭圆的a，b，求椭圆在[L,R]范围内的面积，多组数据

题解

自适应辛普森积分裸题

直接对某个区间进行辛普森积分的话公式为（r - l ）*（f（l ）+4 * f（（ l + r ）/ 2）+f（ r ））/ 6

然后如果直接拆分所求区间的话，如果遇到鬼畜的函数就会使误差变大

所以就有了自适应辛普森积分

就是说我们求这个区间的辛普森积分和左右部分的辛普森积分

如果相差小于eps的话，就直接返回答案

否则递归计算左右区间

就酱

代码

#include<cstdio>
#include<iostream>
#include<cmath>
#define db double
using namespace std;

db a,b,l,r;
int t;

db f(db x)
{
    return sqrt(b*b*(1.0-x*x/a/a));
}

db xin(db l,db r)
{
    db mid=(l+r)/;
    return (r-l)*(f(l)+*f(mid)+f(r))/6.0;
}

db getans(db x,db y,db eps,db val)
{
    db mid=(x+y)/;
    db aa=xin(x,mid),bb=xin(mid,y);
    if(fabs(val-aa-bb)<=eps*15.0) return aa+bb+(aa+bb-val)/15.0;
    return getans(x,mid,eps/2.0,aa)+getans(mid,y,eps/2.0,bb);
}

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lf%lf%lf%lf",&a,&b,&l,&r);
        printf("%.3lf\n",2.0*getans(l,r,0.00005,xin(l,r)));
    }
    return ;
}