K-means算法性能评估及其优化

1、 SSE误差平方和(Sum of Square due to Error)：

聚类情况：

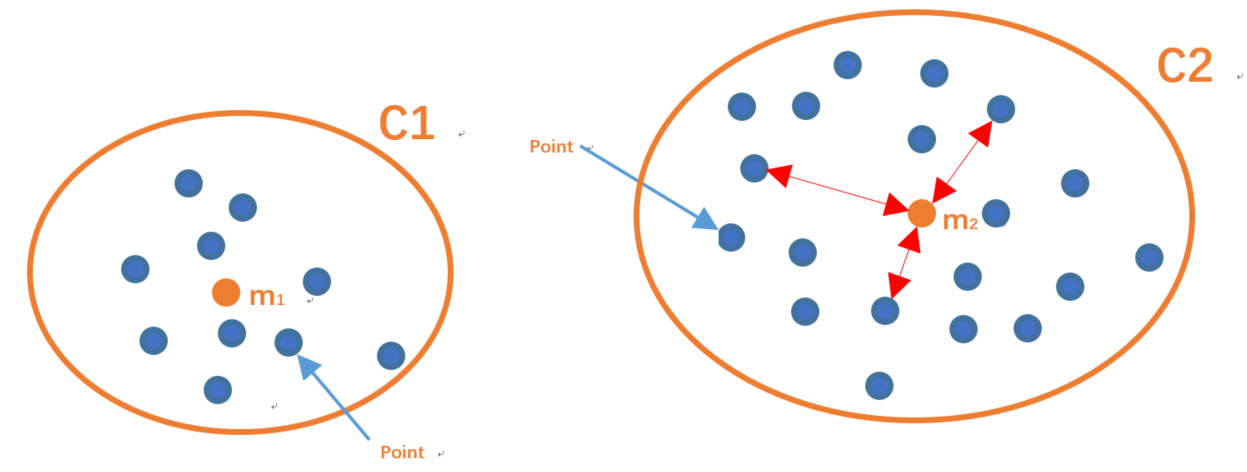
计算公式：

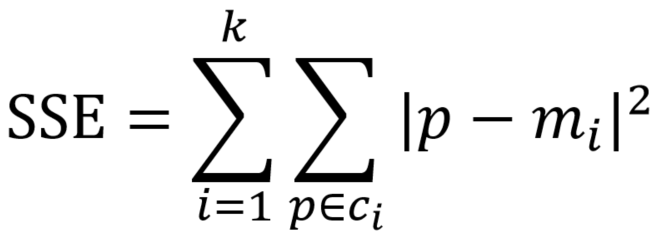
注：SSE参数计算的内容为当前迭代得到的中心位置到各自中心点簇的欧式距离总和，这个值越小表示当前的分类效果越好！

参数描述：

• P表示点位置(x,y)。
• Mi为中心点的位置。
• SSE表示了，当前的分类情况的中心点到自身分类簇的点的位置的总和。

使用方法：

在聚类算法迭代的过程中，我们通过计算当前得到的中心点情况下的SSE值来评估现在的分类效果，如果SSE值在某次迭代之后大大减小就说明聚类过程基本完成，不需要太多次的迭代了，

Code：

 # K-means Algorithm processing the point
 Point_Total = 100 # 某一种类型的总点数
 Error_Threshold = 0.1

 Point_A = (4, 3) # 高斯二维分布中心点
 Point_S_A = (np.random.normal(Point_A[0], 1, Point_Total),np.random.normal(Point_A[1], 1, Point_Total)) # 构造高斯二维分布散点

 Point_B = (-3,2) # 高斯二维分布中心点
 Point_S_B = (np.random.normal(Point_B[0], 1, Point_Total),np.random.normal(Point_B[1], 1, Point_Total)) # 构造高斯二维分布散点

 Point_O = np.hstack((Point_S_A,Point_S_B)) # 所有的点合并在一起

 Origin_A = [Point_O[0][0],Point_O[1][0]]   # 取得K-means算法的起始分类点
 Origin_B = [Point_O[0][20],Point_O[1][20]] # 设置K-means算法的起始分类点

 plt.figure("实时分类") # 创建新得显示窗口
 plt.ion() # 持续刷新当前窗口的内容，不需要使用plt.show()函数
 plt.scatter(Point_O[0],Point_O[1],c='k') # 所有的初始数据显示为黑色
 plt.scatter(Origin_A[0],Origin_A[1],c='b',marker='D') # 显示第一类分类点的位置
 plt.scatter(Origin_B[0],Origin_B[1],c='r',marker='*') # 显示第二类分类点的位置

 Status_A = False # 设置A类别分类未完成False
 Status_B = False # 设置B类别分类未完成False

 CiSum_List = []
 while not Status_A and not Status_B: # 开始分类
         Class_A = [] # 分类结果保存空间
         Class_B = [] # 分类结果保存空间
         print("Seperating the point...")
         CASum = 0
         CBSum = 0
         for i in range(Point_Total*2): # 开始计算分类点到所有点的欧式距离(注意只需要使用平方和即可，不需要sqrt浪费时间)
                 d_A = np.power(Origin_A[0]-Point_O[0][i], 2) + np.power(Origin_A[1]-Point_O[1][i], 2) # 计算距离
                 d_B = np.power(Origin_B[0]-Point_O[0][i], 2) + np.power(Origin_B[1]-Point_O[1][i], 2) # 计算距离
                 if d_A > d_B:
                         Class_B.append((Point_O[0][i],Point_O[1][i])) # 将距离当前点较近的数据点包含在自己的空间中
                         plt.scatter(Point_O[0][i],Point_O[1][i],c='r') # 更新新的点的颜色
                         CBSum += d_B
                 else:
                         Class_A.append((Point_O[0][i],Point_O[1][i])) # 将距离当前点较近的数据点包含在自己的空间中
                         plt.scatter(Point_O[0][i],Point_O[1][i],c='b') # 更新新的点的颜色
                         CASum =+ d_A
                 plt.pause(0.08) # 显示暂停0.08s

         CiSum = CASum + CBSum
         CiSum_List.append(CiSum) # 统计计算SSE的值

         A_Shape = np.shape(Class_A)[0] # 取得当前分类为A集合的点的总数
         B_Shape = np.shape(Class_B)[0] # 取得当前分类为B集合的点的总数
         Temp_x = 0
         Temp_y = 0
         for p in Class_A: # 计算A集合的质心
                 Temp_x += p[0]
                 Temp_y += p[1]
         error_x = np.abs(Origin_A[0] - Temp_x/A_Shape) # 求平均得到重心-质心
         error_y = np.abs(Origin_A[1] - Temp_y/A_Shape)
         print("The error Of A:(",error_x,",",error_y,")") # 显示当前位置和质心的误差
         if error_x < Error_Threshold and error_y < Error_Threshold:
                 Status_A = True # 误差满足设定的误差阈值范围，将A集合的状态设置为OK-True
         else:
                 Origin_A[0] = Temp_x/A_Shape # 求平均得到重心-质心
                 Origin_A[1] = Temp_y/A_Shape
                 plt.scatter(Origin_A[0],Origin_A[1],c='g',marker='*') # the Map-A
                 print("Get New Center Of A:(",Origin_A[0],",",Origin_A[1],")") # 显示中心坐标点

         Temp_x = 0
         Temp_y = 0
         for p in Class_B: # 计算B集合的质心
                 Temp_x += p[0]
                 Temp_y += p[1]
         error_x = np.abs(Origin_B[0] - Temp_x/B_Shape) # 求平均得到重心-质心
         error_y = np.abs(Origin_B[1] - Temp_y/B_Shape)
         print("The error Of B:(",error_x,",",error_y,")")
         if error_x < Error_Threshold and error_y < Error_Threshold:
                 Status_B = True # 误差满足设定的误差阈值范围，将B集合的状态设置为OK-True
         else:
                 Origin_B[0] = Temp_x/B_Shape # 求平均得到重心-质心
                 Origin_B[1] = Temp_y/B_Shape
                 plt.scatter(Origin_B[0],Origin_B[1],c='y',marker='x') # the Map-B
                 print("Get New Center Of B:(",Origin_B[0],",",Origin_B[1],")") # 显示中心坐标点

 print("Finished the divide!")
 print(CiSum_List) # 统计结果
 plt.figure("真实分类")
 plt.scatter(Point_S_A[0],Point_S_A[1]) # The Map-A
 plt.scatter(Point_S_B[0],Point_S_B[1]) # The Map-A
 plt.show()

 plt.figure("SSE Res")
 plt.plot(CiSum_List) # 绘制SSE结果图

 plt.pause(15)
 plt.show()

结果：

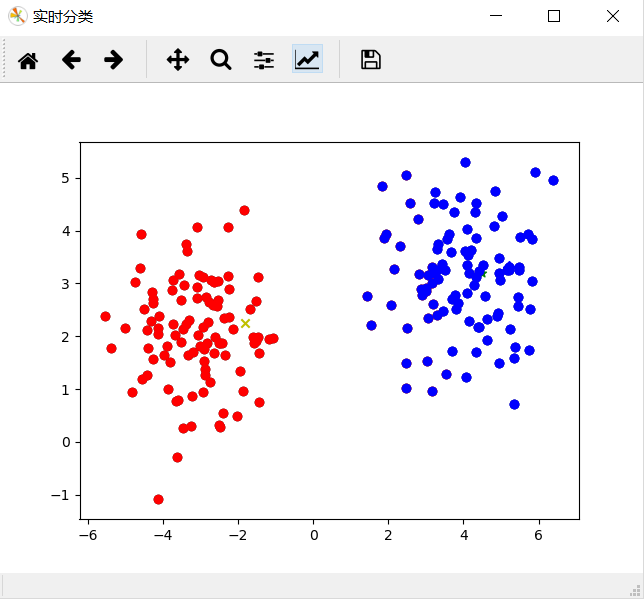
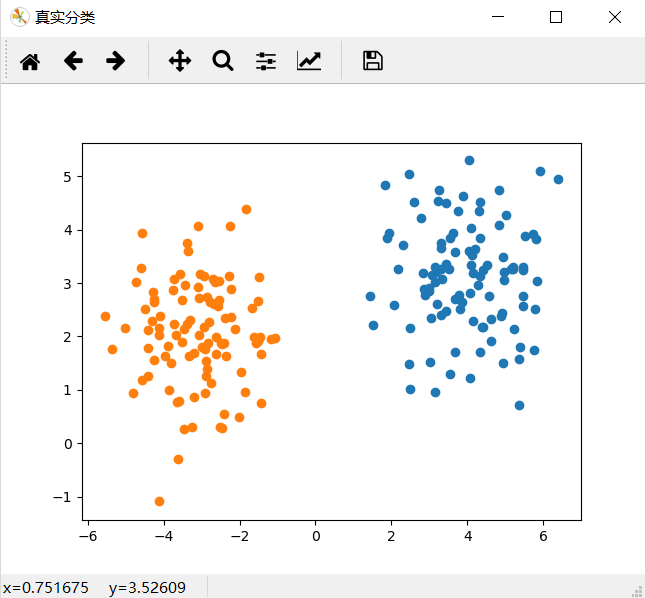
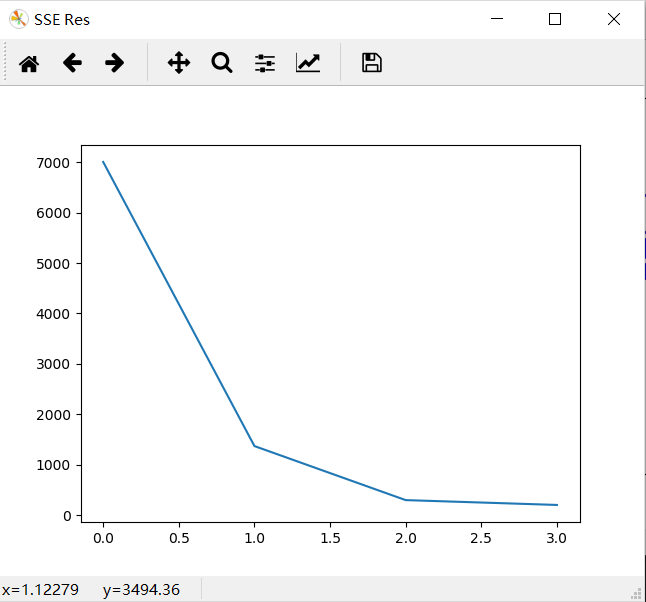
2、 SC系数(Silhouette Cofficient)轮廓系数法：

评估标准描述：结合了聚类的凝聚度(Cohesion)和分离度(Separation),用于评估聚类算法的效果。

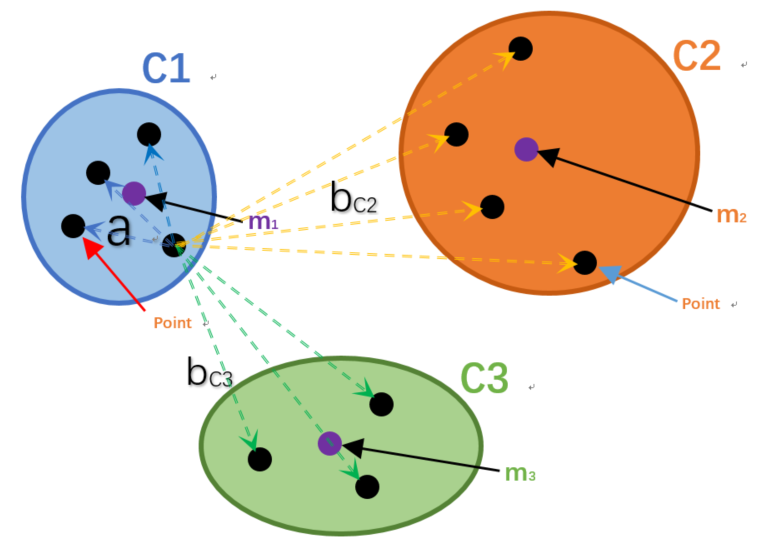
参数描述：

• a表示C1簇中的某一个样本点X_i到自身簇中其他样本点的距离总和的平均值。
• b_C2表示样本点X_i 到C2簇中所有样本点的距离总和的平均值。
• b_C3表示样本点X_i 到C3簇中所有样本点的距离总和的平均值。
• 我们定义b = min(b_C2 ,b_C3)

计算公式：

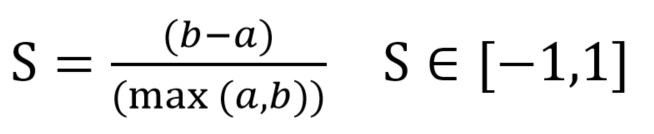
• a：样本Xi到同一簇内其他点不相似程度的平均值
• b：样本Xi到其他簇的平均不相似程度的最小值

使用方法：

每次聚类之后，每一个样本点都会得到一个轮廓系数，当S的取值越靠近1，当前点与周围簇距离较远，结果非常好。

当S的取值为0，说明当前点可能处在两个簇的边界上。

当S的取值为负数时，可能这个点呗误分了。

求出所有样本点的轮廓系数之后再求平均值就得到了平均轮廓系数，平均轮廓系数越大，簇内样本距离越近，簇间样本距离越远，聚类效果越好。

Code：

3、CH系数(Calinski Harabasz Index)轮廓系数法：

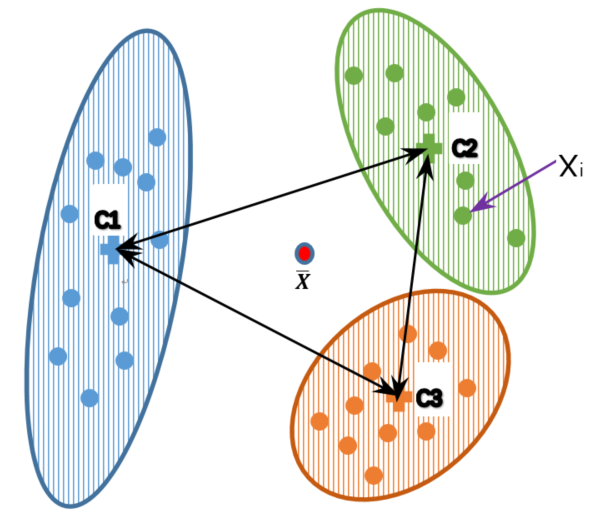
参数描述：

• C1：簇1的中心位置
• C2：簇2的中心位置
• C3：簇3的中心位置
• Xi：簇当中的某一个样本点
• X平均：所有簇当中的样本点的中心位置

计算公式：

 

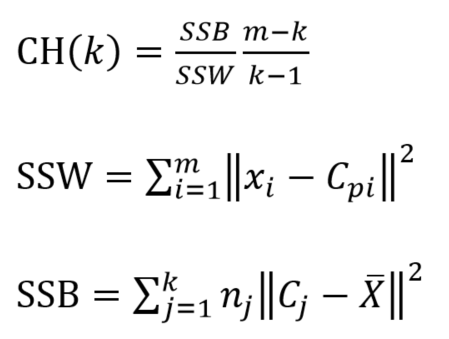
使用方法：

Code：

4、总结：

在我们考量当前的聚类算法的K值选择的问题是，我们会总和汇总上述三种衡量系数来共同确定K值的选择，使得我们选择最好的K值。

如下实例过程，我们来选择合适的K值：

Code：

Result：

分析：