B-Tree与B+Tree简明扼要的区别

原文：https://blog.csdn.net/zhuanzhe117/article/details/78039692

看了很多讲B树和B+树的文章，大多都是围绕各自的特性讲的，第一，树中每个结点最多含有m个孩子（m>=2）；第二，……我也是从这些文章里弄懂了各种树的联系与区别，要真写，我可能还不如人家写得好。所以就在这里简明扼要的用几张图记录一下主要区别吧。

为了便于说明，我们先定义一条数据记录为一个二元组[key,data]，key为记录的键值，key唯一；data为数据记录除key外的数据。

B树

每个节点都存储key和data，所有节点组成这棵树，并且叶子节点指针为null。

B+树

只有叶子节点存储data，叶子节点包含了这棵树的所有键值，叶子节点不存储指针。

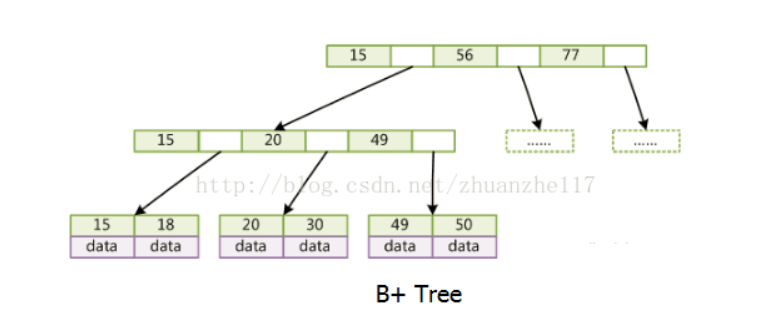
后来，在B+树上增加了顺序访问指针，也就是每个叶子节点增加一个指向相邻叶子节点的指针，这样一棵树成了数据库系统实现索引的首选数据结构。

原因有很多，最主要的是这棵树矮胖，呵呵。一般来说，索引很大，往往以索引文件的形式存储的磁盘上，索引查找时产生磁盘I/O消耗，相对于内存存取，I/O存取的消耗要高几个数量级，所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的时间复杂度。树高度越小，I/O次数越少。

那为什么是B+树而不是B树呢，因为它内节点不存储data，这样一个节点就可以存储更多的key。

在MySQL中，最常用的两个存储引擎是MyISAM和InnoDB，它们对索引的实现方式是不同的。

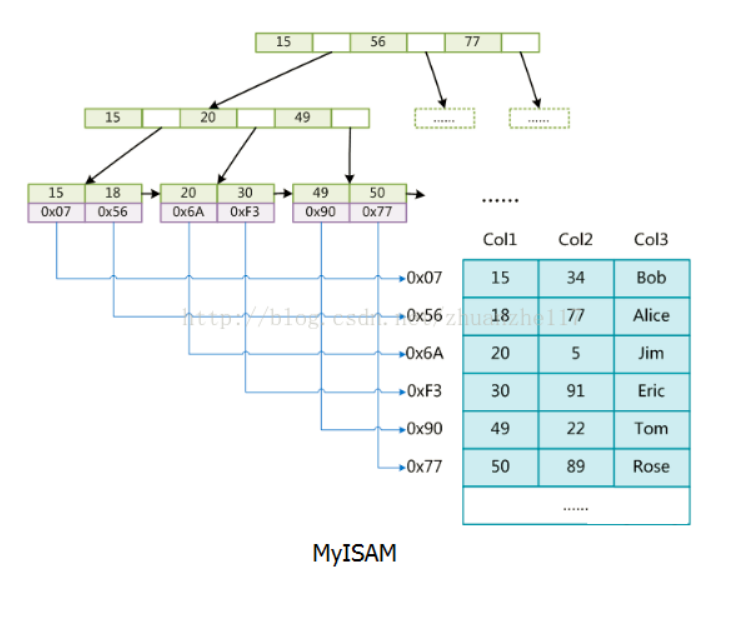
MyISAM

data存的是数据地址。索引是索引，数据是数据。索引放在XX.MYI文件中，数据放在XX.MYD文件中，所以也叫非聚集索引。

InnoDB

data存的是数据本身。索引也是数据。数据和索引存在一个XX.IDB文件中，所以也叫聚集索引。

了解了数据结构再看索引，一切都不费解了，只是顺着逻辑推而已。另加两种存储引擎的区别：

1、MyISAM是非事务安全的，而InnoDB是事务安全的

2、MyISAM锁的粒度是表级的，而InnoDB支持行级锁

3、MyISAM支持全文类型索引，而InnoDB不支持全文索引

4、MyISAM相对简单，效率上要优于InnoDB，小型应用可以考虑使用MyISAM

5、MyISAM表保存成文件形式，跨平台使用更加方便

6、MyISAM管理非事务表，提供高速存储和检索以及全文搜索能力，如果在应用中执行大量select操作可选择

7、InnoDB用于事务处理，具有ACID事务支持等特性，如果在应用中执行大量insert和update操作，可选择。