[2022-2-18] OICLASS提高组模拟赛2 A·整数分解为2的幂

题目链接

问题 A: 整数分解为 2 的幂
题目描述
任何正整数都能分解成 2 的幂，给定整数 N，求 N 的此类划分方法的数量！由于方案数量较大，输出 Mod 1000000007 的结果。
比如 N = 7 时，共有 6 种划分方法。
7=1+1+1+1+1+1+1
=1+1+1+1+1+2
=1+1+1+2+2
=1+2+2+2
=1+1+1+4
=1+2+4

输入
输入一个数 N（1≤N≤10^6)

输出
输出划分方法的数量 Mod 1000000007

样例输入
7
样例输出
6

先放结论:

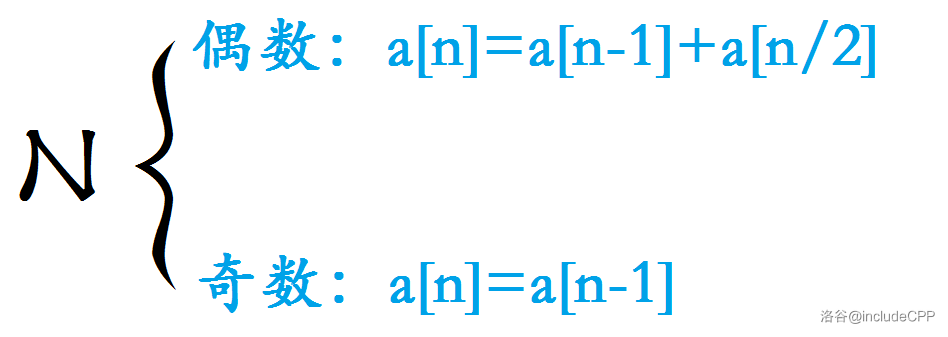
为什么是这样呢？

首先来看 \(N\) 为奇数的情况：

举个例子，6的拆分方法为：

1 1 1 1 1 1
1 1 1 1 2
1 1 2 2
1 1 4
2 2 2
2 4

共6种分解方法。

7的拆分方法呢？

1 1 1 1 1 1 1
1 1 1 1 1 2
1 1 1 2 2
1 1 1 4
1 2 2 2
1 2 4

我们发现，7的拆分在6的拆分的基础上最大的区别即在每组拆分的开头都加上了一个 \(1\) 。

这个多出来的 \(1\) 理论上是可以和其它的 \(1\) 合并的，然并卵，我们发现，当：

1 1 1 1 1 1 1

合并一次后得到

1 1 1 1 1 2

时，本质上与原来的

1 1 1 1 1 2

没有任何区别。那么，我们就得到了第一条结论：

\[当N为奇数时，a[n]=a[n-1]
\]

我们再来看偶数

举个例子，还是6的分解方法：

1 1 1 1 1 1
1 1 1 1 2
1 1 2 2
1 1 4
2 2 2
2 4

我们把它分为有 \(1\) 的拆分部分和没有 \(1\) 的拆分部分

先看有 \(1\) 的拆分部分：

1 1 1 1 1 1
1 1 1 1 2
1 1 2 2
1 1 4

我们发现，把每一种拆分的第一个 \(1\) 盖住之后，我们会发现这与5的拆分方式没有本质上的区别，和奇数一样，我们得到了第一个部分：

\[a[n]=a[n-1]
\]

再看没有1的部分，

2 2 2
2 4

因为拆分的全都是2的次幂，当1即 \(2^0\) 没有后，我们把拆分的每一项的每一个数除以2得：

1 1 1
1 2

我们发现，这本质上就是3的拆分，那么，我们就得到了第二个结论：

\[a[n]=a[n/2]
\]

把两个部分加起来，就得到了偶数的个数公式：

\[a[n]=a[n-1]+a[n/2]
\]

那么看下代码：

#include<iostream>
using namespace std;
long long a[1000010];
int main(){
    long long n;
    a[1]=1;
    for(long long i=2;i<=1000005;i++){
        if(i%2==1){
            a[i]=a[i-1]%1000000007;
        }
        else{
            a[i]=(a[i-1]+a[i/2])%1000000007;
        }
    }
    cin>>n;
    cout<<a[n];
    return 0;
}

The End.

[发布编辑时间]2022/2/18 20:52