2021夏季学期华清大学EE数算OJ1：算数问题

第一次写博客，有点紧张。。。

也许格式也没有特别丑吧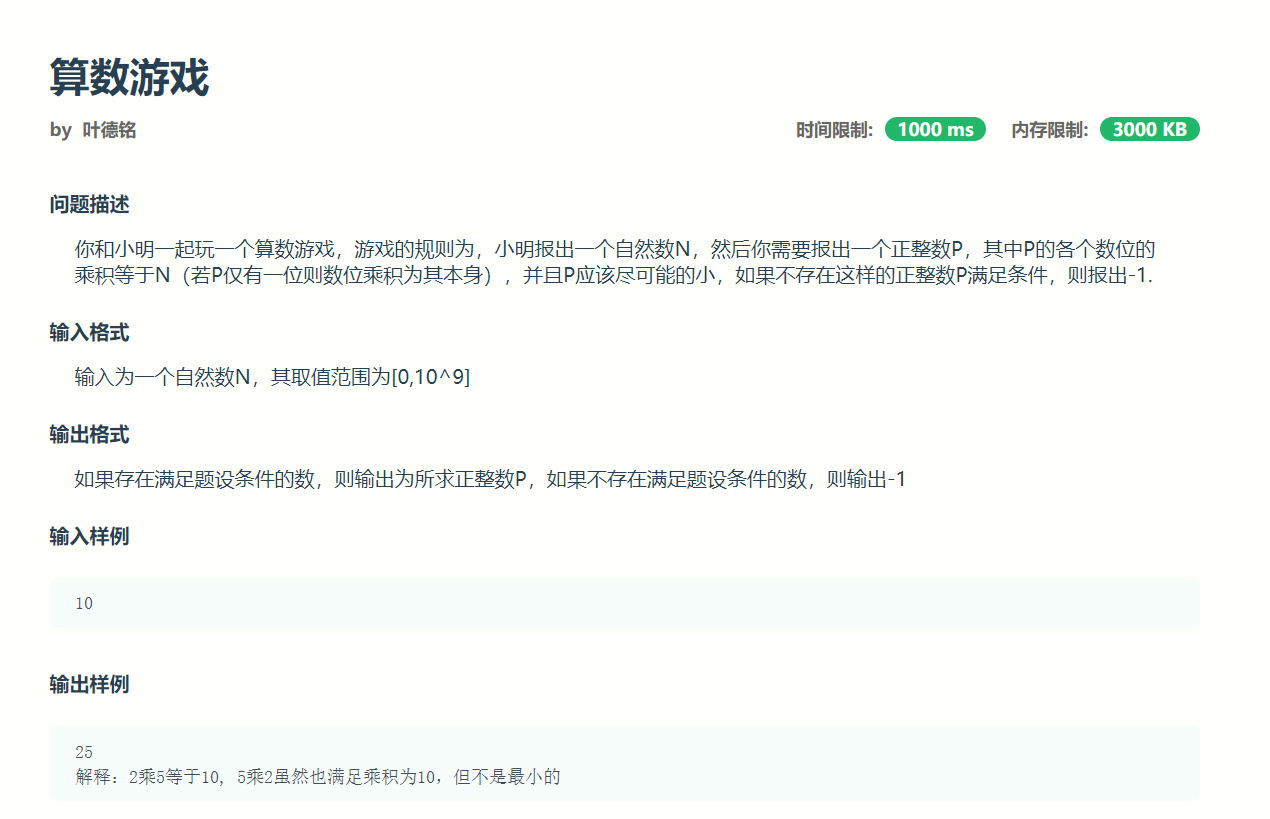

先看原题（

此题做法众多，这里仅仅介绍蒟蒻的一种很复杂的思路（但最后还是喜提0ms的好成绩）

读完这道题，不难发现，此题不过是一个质因数分解+一堆特判

1.质因数分解

作为无系的优秀学子，我们很自然的联想到《程序设计基础》中曾经多次出现的质因数分解。毕竟，本题要求我们输出的各个数位都是原数的因数，那么求解因数的方法在我们的思维中首先就是分解质因数啦。

此外，如果我们愿意多花一小段时间分析，我们也不难看出，如果输入的数字分解质因数后存在11或者更大的质因数，那么一定是不满足题目要求的！直接输出-1即可。

那么，对于其他的数字，其分解质因数的结果只能有：2,3,5,7；

比如，对于数字100，有质因数分解数列：2 2 5 5

因此，2255是满足题目条件的一个数。

2.合并质因数，减少数位

为了让数字最小，我们自然要让数位越小越好。对于2和3，有2*2*2=8,3*3=9,2*3=6，得到的仍然是一位数。那么，如果我们把原质因数列中的2和3合并起来，是不是就达到减少数位的目的了呢？

比如上述的2255，如果我们把2*2合并成4，得到455，其实就达到了减少数位的目的。

对于其他的乘法，自然也是一样的。

但是，对于众多的2和3，我们有很多合并的方式，但我们分析得出：当合并出的因数最大时，对我们减小数字是最有利的。

比如：72=2*2*2*3*3，我们最好的方法是89，而非其他的方案。

此处应用到简单的数学知识，自然难不倒作为无系dalao的你吧。

3.对数列进行排序，取得最小数

在进行第二步之前，由于我们在质因数分解时得到的数列是有序的，我们得到的数满足是“当前数位组成下的最小的数”。但是，合并数位后，我们得到的数字也许不再是有序的。

我采用的办法是，多开了一个数组，在合并质因数的时候直接在原数组中删去因数，在新数组中得到积，这样省去了繁琐的数组坐标移动过程。

然后再把两个数组拼接起来，用sort函数进行排序，就得到符合题意的最小数啦。

4.彩蛋

当我们兴致勃勃的开始评测的时候：

好似！开香槟喽！

结果：

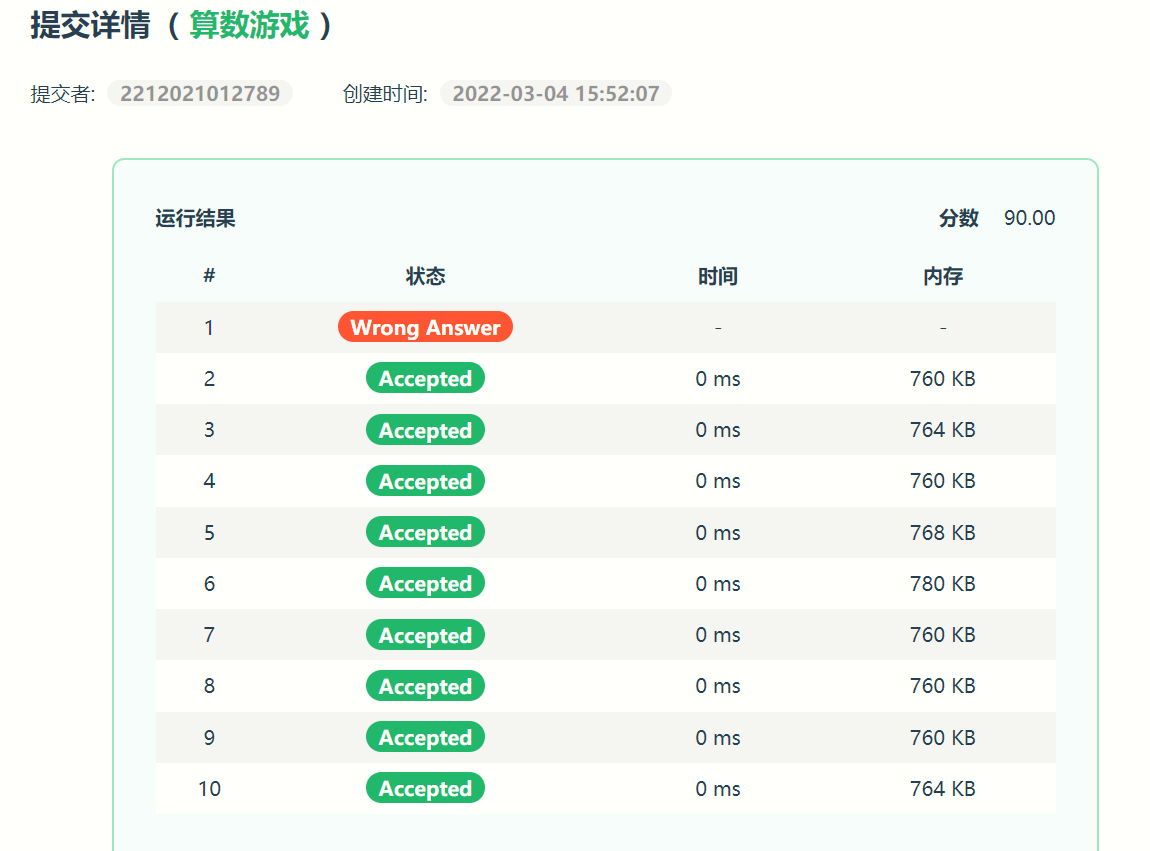
作为无系oj的第一题，本题为大家准备了意外惊喜

我们从小就学过，自然数=正整数+0，那么再去阅读题干，聪明的你一定发现了出题人的深意吧！

附：AC代码

#include<cstdio>
#include<algorithm>
using namespace std;
int a[100],b[100];
int main(){
    int n;
    scanf("%d",&n);
    if(!n){printf("10");return 0;}
    if(n<10){printf("%d",n);return 0;}
    int i,t=1;
    for(int i=2;i*i<=n;i++){
        while(!(n%i)){
            a[t++]=i;n/=i;
        }
    }
    if(n>1)a[t++]=n;
    int l2=0,r2=0,r3=0,l3=0,q=1,bq=0;
    for(int i=1;i<t;i++){
        if(a[i]==2&&(!l2))l2=i;
        if(a[i]==2&&a[i+1]!=2)r2=i;
        if(a[i]==3&&(!l3))l3=i;
        if(a[i]==3&&a[i+1]!=3)r3=i;
        if(a[i]>3&&(!bq)){q=i;bq=1;}
        if(a[i]>9){printf("-1");return 0;}
    }
    int num2=0,num3=0,bnum=1;
    for(int i=l3;i<=r3&&r3>0;i++){
        num3++;
        if(num3==2){
            b[bnum++]=9;
            num3=0;
        }
    }
    for(int i=l2;i<=r2&&r2>0;i++){
        num2++;
        if(num2==3){
            b[bnum++]=8;
            num2=0;
        }
    }
    if(num2&&num3){b[bnum++]=6;num2--;num3--;}
    if(num2==2){b[bnum++]=4;num2-=2;}
    if(num3){b[bnum++]=3;num3--;}
    if(num2){b[bnum++]=2;num2--;}
    for(int i=t;i<t+bnum-1;i++)a[i]=b[i-t+1];
    sort(a+q,a+bnum+t-1);
    for(int i=q;i<t+bnum-1;i++)printf("%d",a[i]);
}

下次会好好调整格式的