python牛顿法求一元多次函数极值

现在用牛顿法来实现一元函数求极值问题

首先给出这样一个问题，如果有这么一个函数$f(x) = x^6+x$，那么如何求这个函数的极值点

先在jupyter上简单画个图形

%matplotlib inline
import numpy as np
x = np.linspace(-1.3,1.3,1000)
plt.scatter(x,x**6+x)
plt.show()

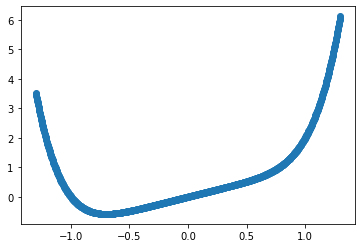
用牛顿法求极值的话，那就要用到泰勒展开

$f(x) \approx f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2}f''(x_0){(x-x_0)}^2$

注意，这里的$x_0$是一个起始点，我们要求$x$，而极值点必须要$f'(x)=0$，而不是这里面的$f'(x_0)=0$，所以这里我们左右两边进行求导，得到

$f'(x)=f'(x_0)+f''(x_0)(x-x_0)$

这里令$f'(x)=0$，则$f'(x_0)+f''(x_0)(x-x_0)=0$，那么即可得到$x = x_0-\frac{f'(x_0)}{f''(x_0)}$，一直迭代则得到

$x_{n+1} = x_n-\frac{f'(x_n)}{f''(x_n)}$

那么我们可以设置一个精度，如果在精度范围内，即可停止迭代

# 牛顿法求极值
# 函数为x**6+x
# orgin函数是初始函数
def func_origin(x):
    result = x**6+x
    return result

# first是一阶导函数
def func_first(x):
    result = 6*x**5+1
    return result

# second是二阶导函数
def func_second(x):
    result = 30*x**4
    return result

# 迭代，传入精度和初始给定值
def newton(accuracy,x):
    count = 1
    new_x = x
    acc = accuracy + 1
    while acc > accuracy:
        print("final %d round is %.6f"%(count,new_x))
        acc = abs(func_first(new_x))
#         print("acc",acc)
        x_origin = func_origin(new_x)
        x_first = func_first(new_x)
        x_second = func_second(new_x)
        new_x = new_x - x_first/x_second
        count += 1

newton(1e-06,10)

final 1 round is 10.000000
final 2 round is 7.999997
...
final 35 round is -0.698860
final 36 round is -0.698827

同时，因为二阶导可能为0，又或者其他原因，实际上我们可能不去计算二阶导，而把二阶导设置为定值(本例不太适用，可尝试更改一下看看结果)

尝试另外一例，函数为：$f(x) = -x^2+4x$，那么其一阶导为$-2x+4$，其二阶导为$-2$

# 牛顿法求极值
# 函数为-x**2+4*x
# orgin函数是初始函数
def func_origin(x):
    result = -x**2+4*x
    return result

# first是一阶导函数
def func_first(x):
    result = -2*x+4
    return result

# second是二阶导函数
def func_second(x):
    return -2

# 迭代，传入精度和初始给定值
def newton(accuracy,x):
    count = 1
    new_x = x
    acc = accuracy + 1
    while acc > accuracy:
        print("final %d round is %.6f"%(count,new_x))
        acc = abs(func_first(new_x))
#         print("acc",acc)
        x_origin = func_origin(new_x)
        x_first = func_first(new_x)
        x_second = func_second(new_x)
        new_x = new_x - x_first/x_second
        count += 1

在这里我们发现不论初始值设为多少，都是两步到达终点，究其原因，一元二次函数太过简单，非常容易求，比如修改一元二次函数为$f(x) = -4x^2+4x$

# 牛顿法求极值
# 函数为-x**2+4*x
# orgin函数是初始函数
def func_origin(x):
    result = -4*x**2+4*x
    return result

# first是一阶导函数
def func_first(x):
    result = -8*x+4
    return result

# second是二阶导函数
def func_second(x):
    return -8

# 迭代，传入精度和初始给定值
def newton(accuracy,x):
    count = 1
    new_x = x
    acc = accuracy + 1
    while acc > accuracy:
        print("final %d round is %.6f"%(count,new_x))
        acc = abs(func_first(new_x))
#         print("acc",acc)
        x_origin = func_origin(new_x)
        x_first = func_first(new_x)
        x_second = func_second(new_x)
        new_x = new_x - x_first/x_second
        count += 1

newton(1e-06,1.3)

final 1 round is 1.300000
final 2 round is 0.500000

如果还要深究的话，想要弄明白为什么前面的一元六次函数要迭代那么多次，而一元二次函数总是只要两次

就需要弄明白泰勒展开，因为一开始我们的一元六次对应的泰勒展开，是近似的，实际上展开的三次及以上被我们抛弃了

而这些三次项，在我们后面的一元二次函数中，是高阶无穷小，舍去对结果无影响，自然只需要两次即可

牛顿法在西瓜书上公式3.29中就有应用，就是用的当前点减去二阶导分之一阶导