正睿十一A班模拟赛day1

估分：25+0+60=85

实际：25+0+60=85

T1：

　　就只会25的暴力

　　分治，到一个区间[l,r]，cnt[i]表示i这个颜色在区间内的出现次数，从两头同时扫描，扫描到第一个cnt[i]小于f[r-l+1]后往下走，先继续搜较大的区间，再搜索小区间，返回时把cnt清空，因为已经搜过了就没必要搜了

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6
 7 const int N = 1000010;
 8
 9 int n;
10 int c[N], f[N], cnt[N];
11
12 int ans;
13
14 void dfs(int l, int r)
15 {
16     for (int i = l, j = r; i <= j; i++, j--)
17     {
18         if (cnt[c[i]] < f[r - l + 1])
19         {
20             for (int k = l; k <= i; k++) cnt[c[k]]--;
21             dfs(i + 1, r);
22             for (int k = l; k < i; k++) cnt[c[k]]++;
23             dfs(l, i - 1);
24             return;
25         }
26         if (cnt[c[j]] < f[r - l + 1])
27         {
28             for (int k = r; k >= j; k--) cnt[c[k]]--;
29             dfs(l, j - 1);
30             for (int k = r; k > j; k--) cnt[c[k]]++;
31             dfs(j + 1, r);
32             return;
33         }
34     }
35
36     ans = max(ans, r - l + 1);
37     for (int i = l; i <= r; i++) cnt[c[i]]--;
38 }
39
40 int main()
41 {
42     scanf("%d", &n);
43     for (int i = 1; i <= n; i++) scanf("%d", &c[i]), cnt[c[i]]++;
44     for (int i = 1; i <= n; i++) scanf("%d", &f[i]);
45     dfs(1, n);
46     printf("%d", ans);
47 }

T2：

　　可能有个10分的暴力，但没写完

T3：

　　因为有一个k的宽容，经过简单的推理过程就能得出答案至少为n-1，60分就到手了，若n=9,构造就这样

　　0 1 2 3 4 5 6 7 8

　　8 7 6 5 4 2 1 0 3

　　a正序，b逆序，把b[n/2+1]挪到最后

　　正解：

　　当n=4k+2或n=4k+3时就是上面的构造方法，不存在答案为n的构造，证明如下：
　　

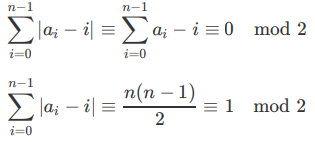
　　当n=4k时，设构造出的排序为a，我们把a_i和i连边，就会得到下面这样的环：

　　

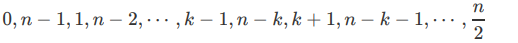
　　当n=4k+1时，可以得到这样的环：

　　

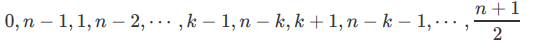
　　可以看出a_i,和b_i的差值都是不同的

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6
 7 const int N = 1000010;
 8
 9 int n, k;
10 int t1, t2, p[N], sz;
11 char c[10];
12
13 void write(int x)
14 {
15     if (x < 0) putchar('-'), x = -x;
16     if (x / 10) write(x / 10);
17     putchar(x % 10 + '0');
18 }
19
20 int main()
21 {
22     scanf("%d%d", &n, &k);
23     t1 = 1, t2 = n;
24
25     if ((n & 3) > 1)
26     {
27         for (int i = 1; i <= (n >> 1); ++i)
28         {
29             p[t1] = t2;
30             p[t2] = t1 + 1;
31             t1++, t2--;
32         }
33         p[t1] = 1;
34     }
35     else
36     {
37         for (int i = 1; t1 < t2; ++i)
38         {
39             p[t1] = t2;
40             if (t1 == (n >> 2)) p[t1 + 1] = t1 + 1, ++t1;
41             p[t2] = t1 + 1, ++t1, --t2;
42         }
43         p[t1] = 1;
44     }
45     for (int i = 1; i <= n; ++i) write(i - 1), putchar(' ');
46     puts("");
47     for (int i = 1; i <= n; ++i) write(p[i] - 1), putchar(' ');
48 }