为C量身定制的Matrix库

Matrix库的诞生让矩阵操作在C中也可以玩的很溜！

项目地址：https://github.com/SJ2050SJ/Matrix

文章目录

• Matrix的设计框架
• Matrix的上手简历

Matrix的设计框架

---

Matrix库中，矩阵的存储结构采用的是链表和数组结合的形式，矩阵的每一行串成一个链表，而每一行的数据则采用的数组进行存储，最终的结果是平均了链表和数组的优缺点。Matrix库中采用的是二维double类型的矩阵（未来可能会根据需求拓展到高维矩阵上去），支持矩阵的加减、乘、转置、换行、数乘、累加、求逆、求行列式、解线性方程组等基本操作，总之，这个库我认为很棒！

Matrix的上手简历

这里将给一段使用Matrix库求解一组线性方程的例子：

#include <stdio.h>
#include <stdlib.h>
#include "matrix.h"

int main()
{
	/*求解一下线性方程组：
		| 2x1 - x2 - x3 + x4 = 2,
		| x1 + x2 - 2x3 + x4 = 4,
		< 4x1 - 6x2 + 2x3 - 2x4 = 4,
		| 3x1 + 6x2 - 9x3 + 7x4 = 9.*/
	double A[4][4] = {
		{2,-1,-1,1},
		{1,1,-2,1},
		{4,-6,2,-2},
		{3,6,-9,7}
	};	// 系数矩阵A的数据
	double b[4][1] = {
		{2},
		{4},
		{4},
		{9}
	};	// 右边常数项矩阵b的数据

	pMatrixRow *matrixRowsOfA, *matrixRowsOfb;	//	矩阵的每行
	pMatrix matrixA, matrixb, resultx;	// A、b矩阵以及结果的x向量

	matrixRowsOfA = (pMatrixRow*)malloc(sizeof(pMatrixRow) * 4);
	matrixRowsOfb = (pMatrixRow*)malloc(sizeof(pMatrixRow) * 4);

	// 矩阵每行初始化
	for (int i = 0; i < 4; i++) {
		matrixRowsOfA[i] = (pMatrixRow)malloc(sizeof(MatrixRow));
		matrixRowsOfA[i]->row = A[i];

		matrixRowsOfb[i] = (pMatrixRow)malloc(sizeof(MatrixRow));
		matrixRowsOfb[i]->row = b[i];
	}

	// A，b矩阵初始化
	matrixA = MatrixInit(matrixRowsOfA, 4, 4, true);
	matrixb = MatrixInit(matrixRowsOfb, 4, 1, true);
	// 线性方程组求解
	resultx = SolveLinearEquations(matrixA, matrixb);

	printf("|2x1 - x2 - x3 + x4 = 2,\n\
| x1 + x2 - 2x3 + x4 = 4,\n\
< 4x1 - 6x2 + 2x3 - 2x4 = 4,\n\
| 3x1 + 6x2 - 9x3 + 7x4 = 9.\n");
	printf("上述方程的解为：\n");

	//	打印矩阵
	MatrixPrint(resultx,6);
	// 清理矩阵
	MatrixCleanAll();
	system("pause");
    return 0;
}

上面简短的代码中我们便成功求解了一个线性方程组，这里我们只需搞清楚MatrixRow和Matrix的区别（pMatrixRow和pMatrix是MatrixRow和Matrix的指针形态），前者是指矩阵的一行，后者代表整个矩阵，矩阵的初始化就是把矩阵每一行的MatrixRow传入MatrixInit函数中，其便会返回初始化后的矩阵。

       你可能对上面的MatrixCleanAll函数产生好奇，是的，这个库中实现了自动清理机制，调用该函数便会清理所有矩阵，大大降低了内存溢出的可能性。其还有个兄弟函数——MatrixClean，这个函数尽会清理重要级别为false的矩阵，这也就意味着，我们可以使用随用随销的矩阵，而不必为给每个矩阵变量起名字而苦恼。

       上述程序的运行动图如下：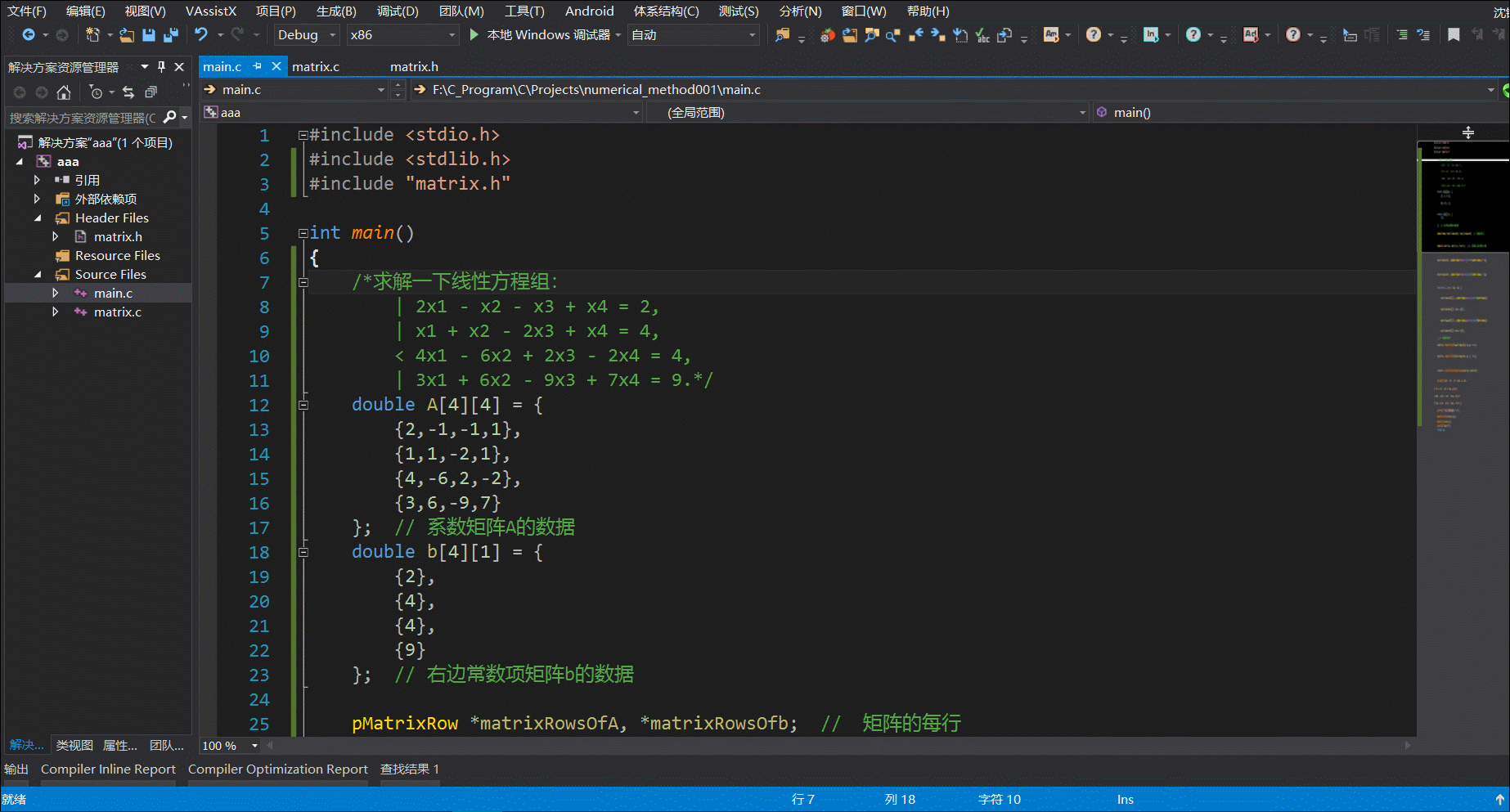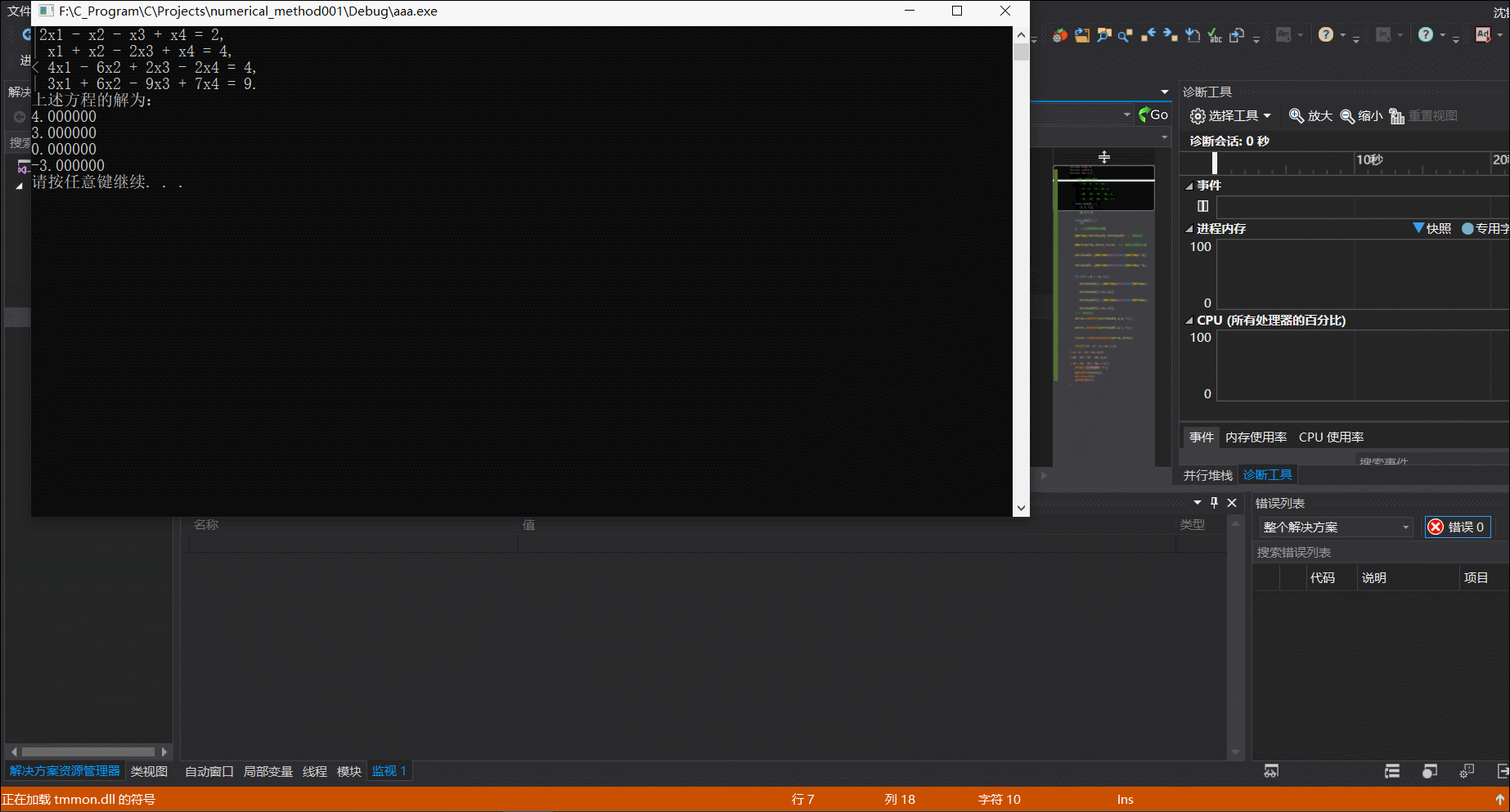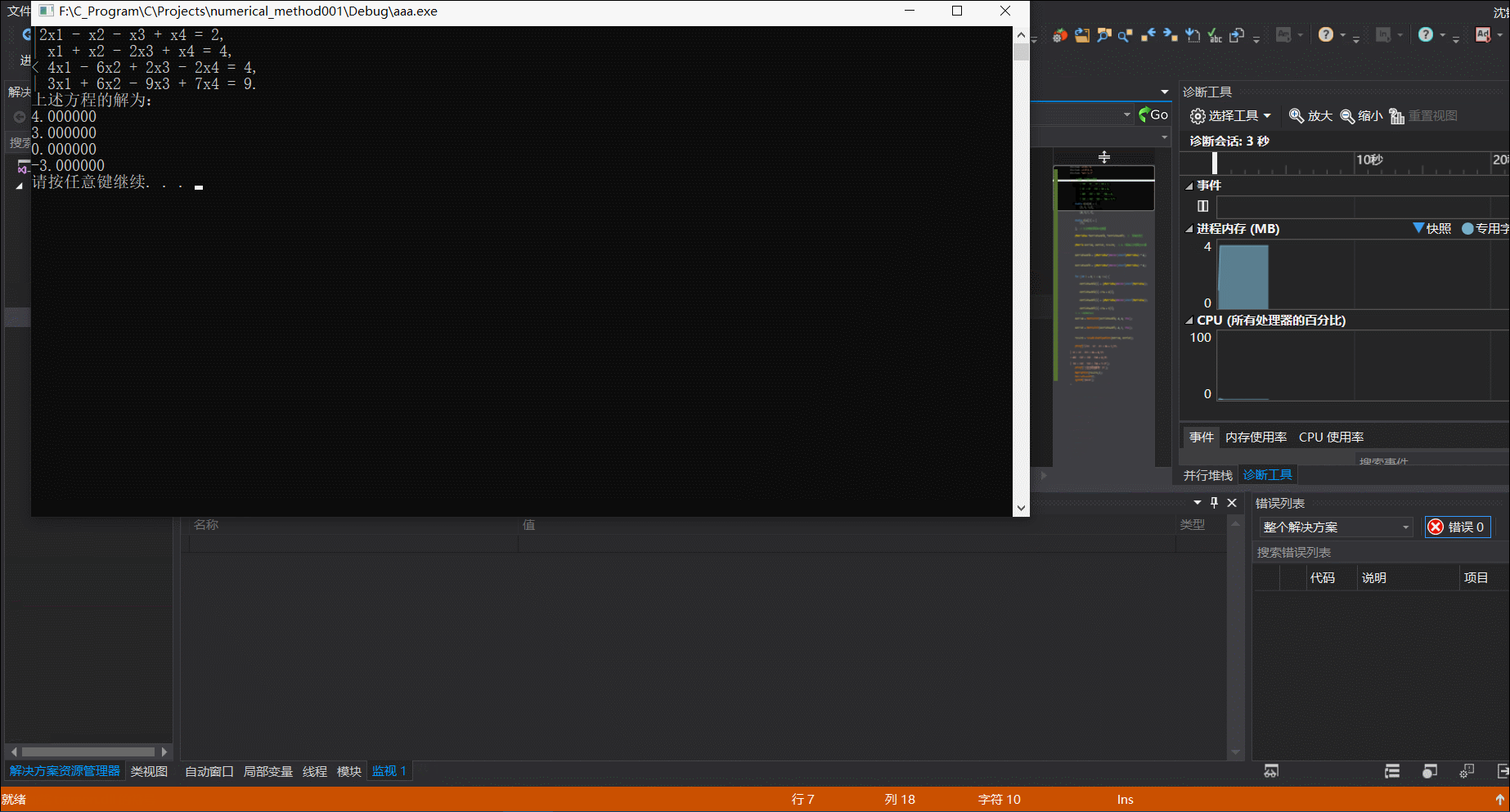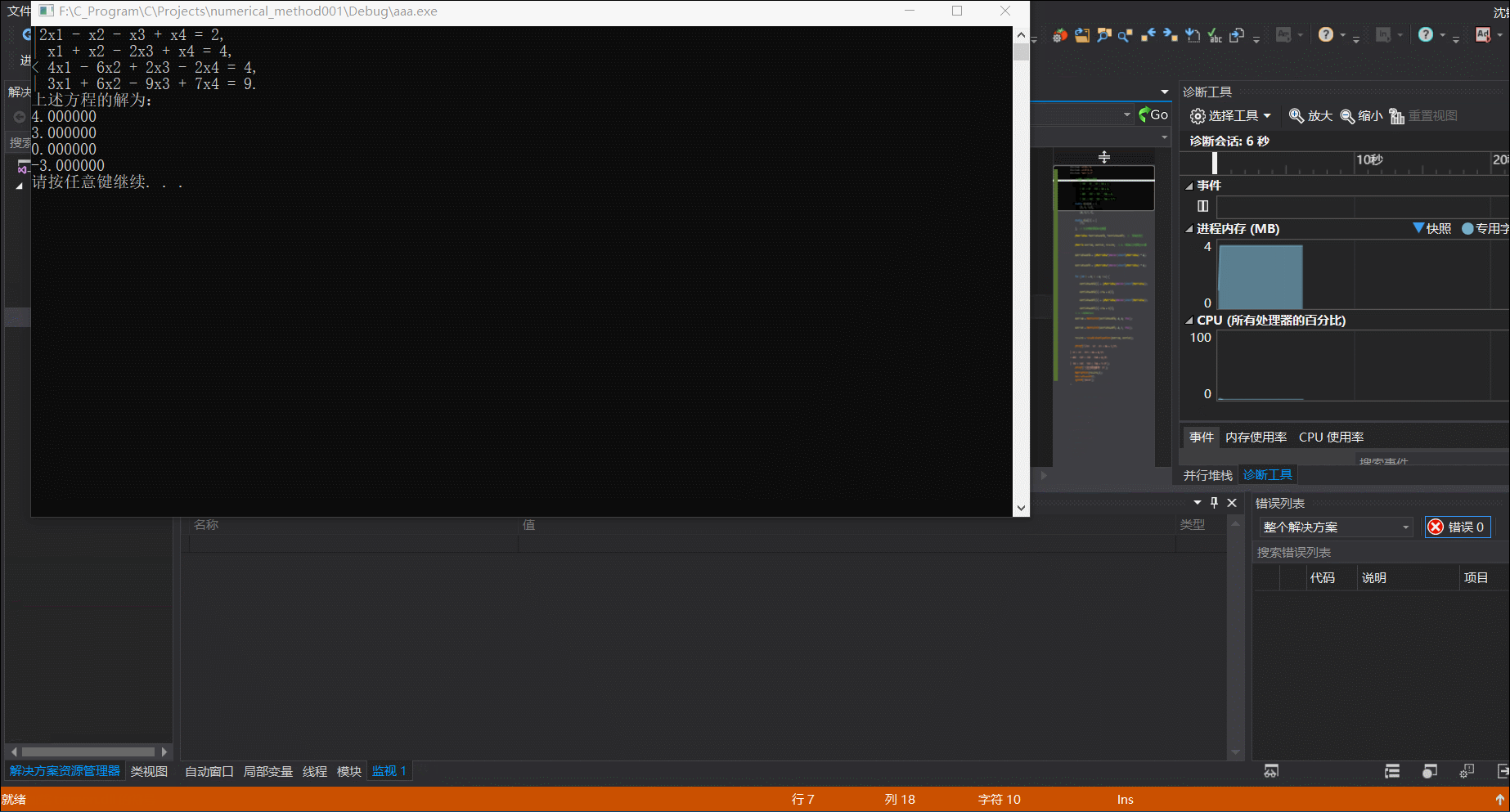

 

 

 

 

 

 

       最后再来感受一下自动清理机制的魅力：

                                                 开启自动清理前



                                                 开启自动清理后