Boltzmann Machine 玻尔兹曼机入门

Generative Models

生成模型帮助我们生成新的item，而不只是存储和提取之前的item。Boltzmann Machine就是Generative Models的一种。

Boltzmann Machine

Boltzmann Machine和Hopfield Network对比

• Energy Function是相同的
• 神经元\(x_i\)的取值在0和1之间，而不是Hopfield Network中的-1和1。
• 使用Boltzmann Machine来产生新的状态，而不是提取存储的状态。
• 更新不是确定性的，而是随机性的，使用Sigmoid函数。

Boltzmann Distribution

Boltzmann Distribution是一种在状态空间上的概率分布，公式如下：

\[p(x) = \frac{e^{\frac{-E(x)}{T}}}{Z}
\]

• \(E(x)\)：energy function
• T：是温度
• Z：partition function，用来保证\(\sum_x p(x)=1\)

通常情况下，直接计算partition function很复杂。但是我们可以利用相邻状态的相对概率通过迭代过程从分布中采样。

Gibbs Sampling

参考博客：https://www.cnblogs.com/aoru45/p/12092453.html

假设我们有一个图像x，对于所有的元素\(x_i=1\)。每一次操作，我们只将一个\(x_i\)变为0，其他的不变，从而得到一个新的图像。

我们用如下的公式来表示两个图像之间的energy function的差：

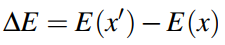
我们可以得到新图像的Boltzmann Distribution，如下：

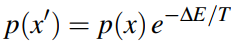
因此，对于所有固定的元素，\(x_i\)取得1或者0的概率如下所示：

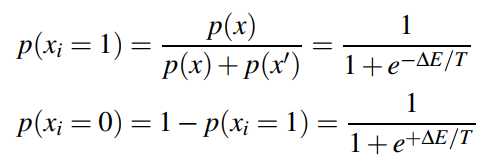
Boltzmann Machine

Boltzmann Machine的操作和Hopfield Network很像，只是再更新神经元的步骤上又差别！Boltzmann Machine在神经元更新的时候有随机性。

在Hopfield Network中， \(x_i\)的变化使得energy function永远不会增大。但是在Boltzmann Machine中，我们用一个概率来令\(x_i=1\)：

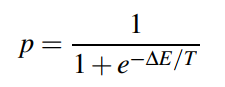
换句话说，这个概率有可能让energy function的值变大。所以：

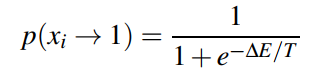
• 如果这个过程重复迭代很多次，我们最终将会获得一个Boltzmann Distribution中的样本

• 当\(T\rightarrow \infty\)，\(\space p(x_i\rightarrow1)=1/2\)并且\(\space p(x_i\rightarrow0)=1/2\)

• 当\(T\rightarrow 0\)，这个行为将会变得很像Hopfield Network，永远不会让Energy Function增大。\(\space p(x_i\rightarrow1)=0\)

• 温度T可能是一个固定值，或者它一开始很大，然后逐渐的减小（模拟退火，Simulated Annealing）

Limitations

Boltzmann Machine的局限性在于，每个单元的概率必须是周围单元的线性可分函数。所以，我们可以考虑到的解决办法就是增加隐藏层，将可见的单元和隐藏的单元分开。类似于前馈神经网络中的输入层和隐藏层。目的就是让隐藏单元学习一些隐藏的特征或者潜在的变量，从而帮助系统去对输入进行建模。结构如下图所示：

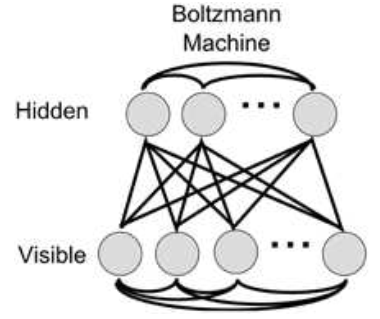
Restricted Boltzmann Machine

如果我们让所有的可见单元之间和隐藏单元之间互相存在连接，训练网络要花非常长的时间。所以，我们通常限制Boltzmannn Machine只在可见单元和隐藏单元之间存在连接，如下图所示：

这样的网络就被称作Restricted Boltzmann Machine，受限玻尔兹曼机。主要特征是：

• 输入是二元向量

• 是两层的双向神经网络

  • 可见层，v，visible layer
  • 隐藏层，h，hidden layer

• 没有vis-to-vis或者hidden-to-hidden连接

• 所有可见单元连接到所有隐藏单元，公式如下：\(E(v, h) = -(\sum_i b_i v_i + \sum_j c_j h_j + \sum_{ij} v_i w_{ij}h_j)\)

  • \(\sum_i b_i v_i\)：可见层偏差
  • \(\sum_j c_j h_j\)：隐藏层偏差
  • \(\sum_{ij} v_i w_{ij}h_j\)：可见单元和隐藏单元之间的连接

• 训练使数据的期望对数概率最大化

因为输入单位和隐藏单位是解耦的，我们可以计算h在v下的条件分布，反之亦然。

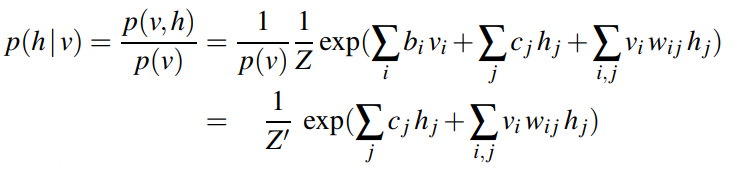
于是，

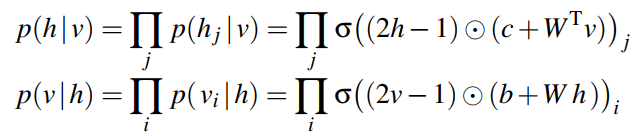
• ：component-wise multiplication
• σ(s) = 1/(1 + exp(-s)) ，是Sigmoid函数

Alternating Gibbs Sampling

在Boltzmann Machine中我们可以从Boltzmann Distribution中进行如下抽样：

• 随机选择\(v_0\)
• 从\(p(h|v_0)\)中抽样\(h_0\)
• 从\(p(v|h_0)\)中抽样\(v_1\)
• 从\(p(h|v_1)\)中抽样\(h_1\)
• ...

Training RBM

Contrastive Divergence

通过对比真实和虚假的图片进行训练，优先选择真实的图片

1. 从训练数据中选择一个或者多个positive samples { \(v^{(k)}\) }
2. 对于每一个\(v^{(k)}\)，从\(p(h|v(k))\)中抽样一个隐藏向量\(h^{(k)}\)
3. 通过alternating Gibbs sampling 生成一个fake样本{\(v'^{(k)}\)}
4. 对于每一个\(v'^{(k)}\)，从\(p(h|v'^{(k)})\)中抽样一个隐藏向量\(h'^{(k)}\)
5. 更新\({b_i}\)，\(c_j\)，\(w_{ij}\)去增大\(log\ p(v^{(k)}, h^{(k)}) - log\ p(v'^{(k)}, h'^{(k)})\)
   • \(b_i \leftarrow b_i + \eta(v_i - v'_i)\)
   • \(c_j \leftarrow c_j + \eta(h_j - h'_j)\)
   • \(w_{ij} \leftarrow w_{ij} + \eta(v_i h_j - v'_i h'_j)\)

Quick Contrastive Divergence

在2000‘s的时候，研究人员注意到，这个过程可以通过只取一个额外的样本来加速，而不是运行多次迭代。

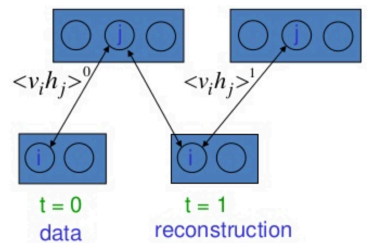
从实数开始，生成隐藏单元，生成假(重构)数字，并分别作为正样本和负样本进行训练

1. \(v_0, h_0\)： positive sample
2. \(v_1, h_1\)：negative sample

Deep Boltzmann Machine

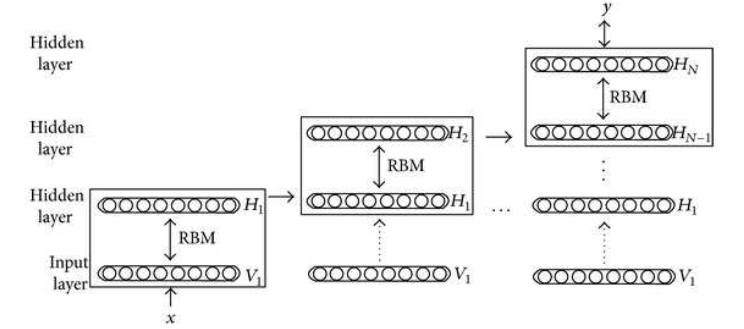
和Boltzmann Machine是相同的方法，但是可以迭代的应用于多层网络。

首先训练输入到第一层的权重。然后保持这些权重不变，继续训练第一层到第二层之间的权重，以此类推。

Greedy Layerwise Pretraining

Deep Boltzmann Machine的一个主要应用是Greedy unsupervised layerwise pretraining（贪婪无监督逐层与训练）。

连续的对每一对layers进行训练，训练成RBM。

当模型训练完成之后，权重和偏差会被储存下来，在下一次进行类似的任务时会被当做前馈神经网络的初始权重和偏差，然后再根据当前任务数据进行反向传播训练。

对于Sigmoid或者tanh激活函数，这一类的预训练能够比直接进行随机初始化权重然后训练取得更好的结果。