【算法•日更•第二期】查找算法：三分VS二分

▎前言：函数

　　如果你已经上过初二的数学课了，那么你十有八九会被函数折磨到吐血，这是一种中考压轴题类的题目，往往分类讨论到你恶心。不过没学过也不打紧，现场讲解一下：

☞『数学中的函数』

　　一般地，如果在一个变化过程中有两个变量x和y，并且对于变量x的每一个值，变量y都有唯一的值与它对应，那么我们称y是x的函数，x是自变量。（copy自八上数学BS教材）

　　表示函数的方法：列表法、关系式法和图像法。（copy自八上数学BS教材）

　　可能有些枯燥，举个例子：小明从家出发，去旅游，速度是2m/s，如果他不歇下来，那么x小时后就会走2x米，如果用y来表示路程，那么就有y=2x，那么y就是x的函数。

　　表示成图像是这样的：

　　

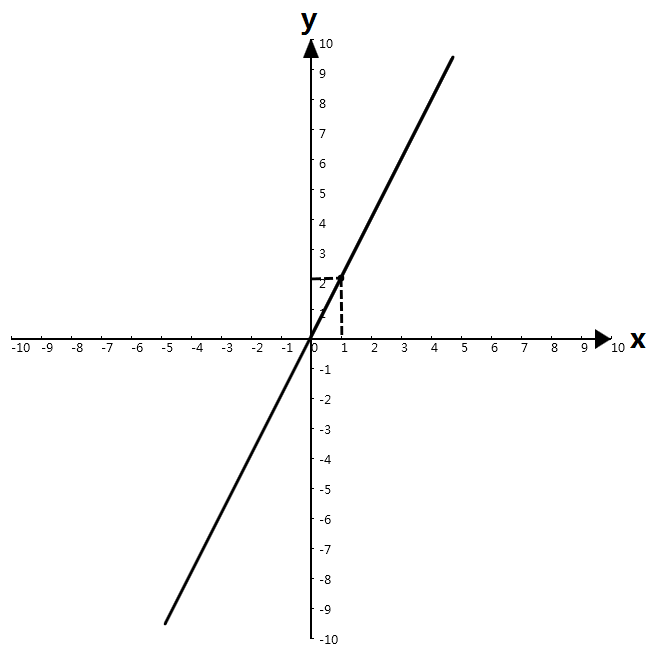
　　细细一看便会发现直线上的点y轴的值总是x轴值的2倍，这就是函数的图像。

　　还有这些：

　　

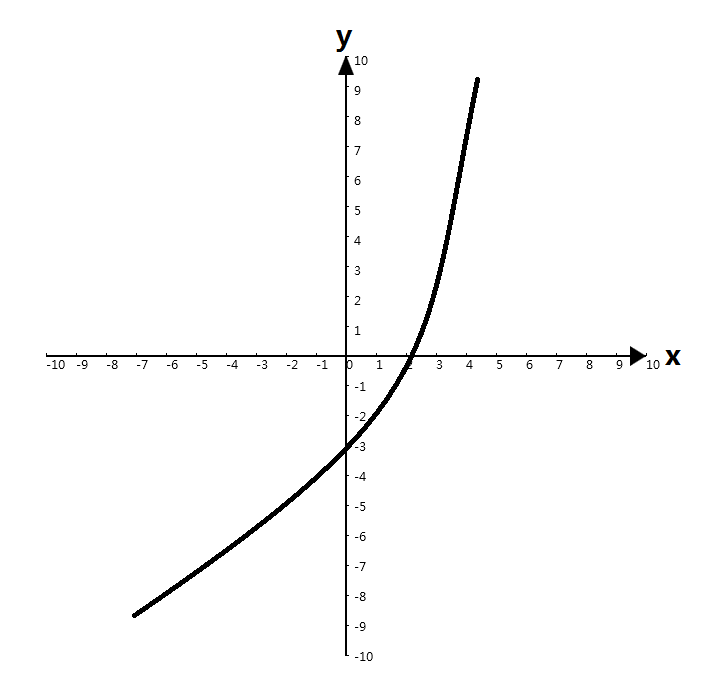
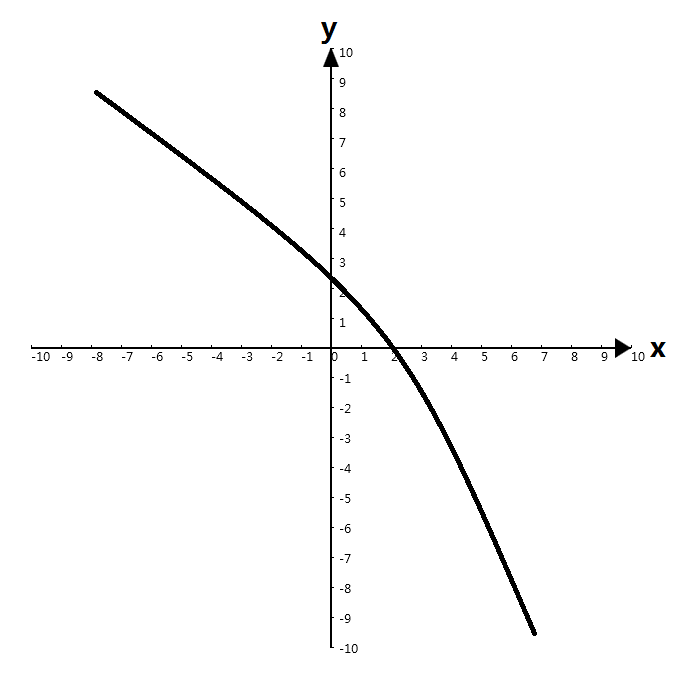
　　像这样的函数都是单调函数。

☞『单调函数』

　　一般的，不强调区间的情况下，所谓的单调函数是指， 对于整个定义域而言，函数具有单调性。而不是针对定义域的子区间而言。举个例子，反比例函数是一个具有单调性的函数，而不是一个单调函数，因为在反比例函数的定义域上，并不呈现整体的单调性。单调函数只是单调性函数中特殊的一种。区间具有单调性的函数并不一定是单调函数，而单调函数的子区间上一定具有单调性。具有单调性函数可以根据区间不同而单调性不同。（copy自百度）

　　这就是定义了，猜你也看不懂，一句话概括：函数y的值随着自变量x的增大而增大或函数y的值随着自变量x的增大而减小，不能出现随着x增大而yx却先增大后减小之类的情况。

☞『单峰函数』

　　单峰函数是在所考虑的区间中只有一个严格局部极大值(峰值)的实值函数。如果函数f(x)在区间[a, b]上只有唯一的最大值点C，而在最大值点C的左侧，函数单调增加；在点C的右侧，函数单调减少，则称这个函数为区间[a, b]上的单峰函数。（copy自百度）

　　单峰函数不太好解释，直接上图吧：

　　

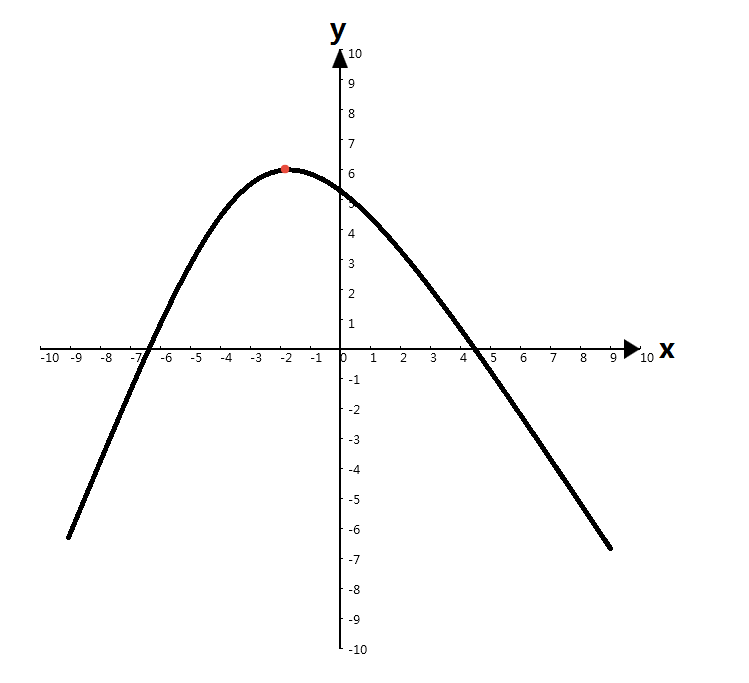
　　红点处就是这个函数的峰，就像山的峰一样，而下图却有两个峰，不属于单峰函数：

　　

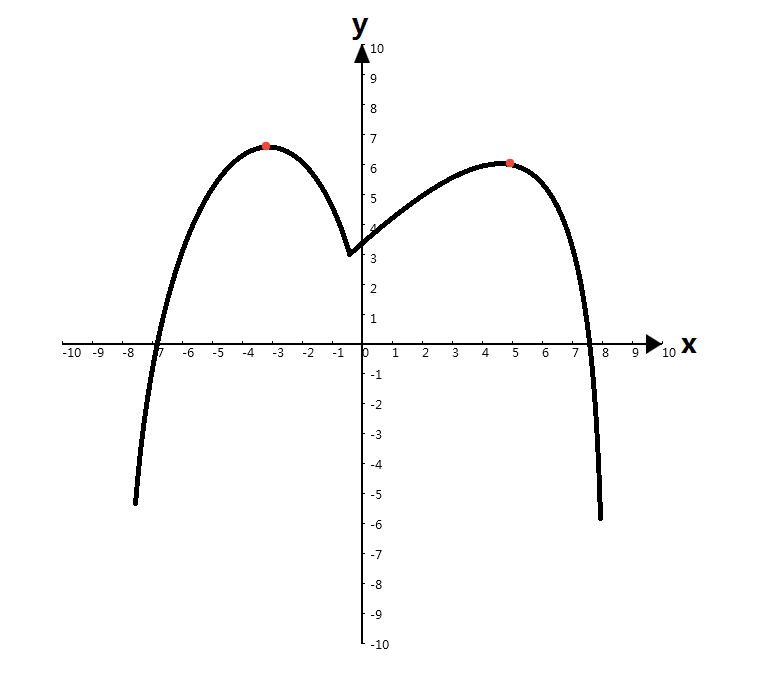
☞『计算机中的函数』

　　函数是指一段在一起的、可以做某一件事的程序。

　　学会了数学上的函数，可别忘了计算机函数了。

---

感觉前言说太多了，赶紧切入正题：

▎算法：二分&单调函数

　　学过二分查找（不会的话戳这里）的人都知道：二分是一种查找值的算法，但是前提是查找的数是已经排好序的（升序降序无所谓），才能二分查找。

　　那么用在函数上时呢？很容易就能辨认出只有单调函数才符合已经排好序。

▎算法：三分&单峰函数

☞『三分』

　　与二分相对比，二分形象一点说是切一刀分成两份，那么三分就是切两刀分成三份，怎么切呢？二分是取中间的（中点），那么三分就是取两个三等分点呗。

　　当出现单峰函数时由于函数值没有排好序，所以二分只会力不从心，而三分则是这类问题的常用算法。

　　三分常常用来找单峰函数峰值。

☞『算法思想』

　　1）取两个三等分点。

　　

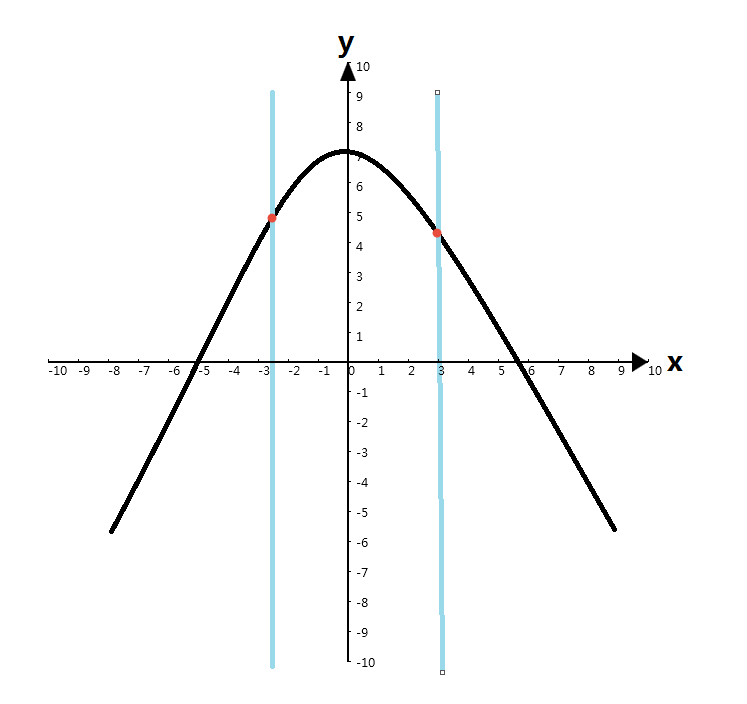
　　2）取中点。

　　

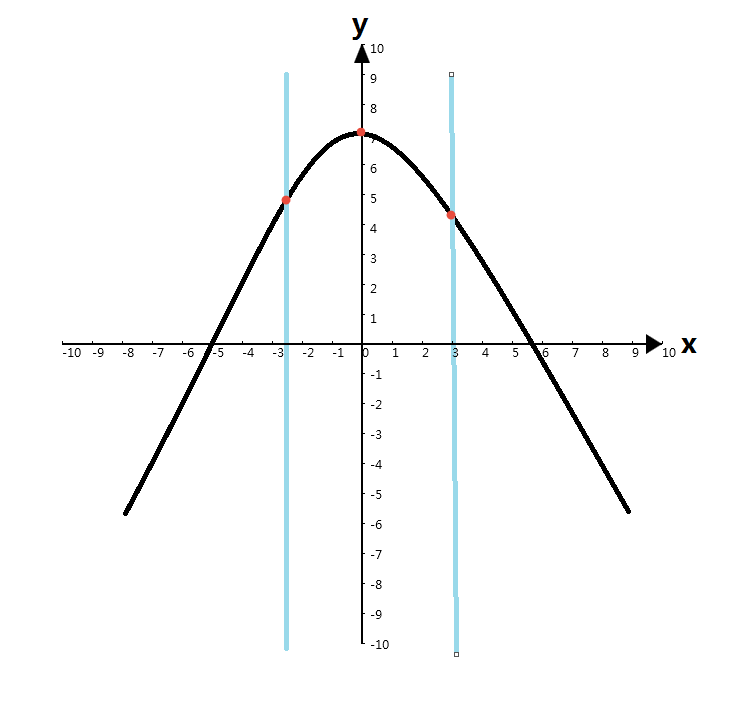
　　3）比较大小。

　　若左边的三等分点大于右边的三等分点，则放弃右区间。

　　否则放弃左区间。

　　4）反复这样，直到找到峰值。