CF-559C Gerald and Giant Chess（计数DP）

给定一个 \(H*W\)的棋盘，棋盘上只有\(N\) 个格子是黑色的，其他格子都是白色的。

在棋盘左上角有一个卒，每一步可以向右或者向下移动一格，并且不能移动到黑色格子中。求这个卒从左上角移动到右下角，一共有多少种可能的路线

\(1\le H,W\le 10^5,1\le N\le 2000\) 输出对\(10^9+7\)取模

H，W巨大，普通DP不用想，考虑如何用黑格子计数

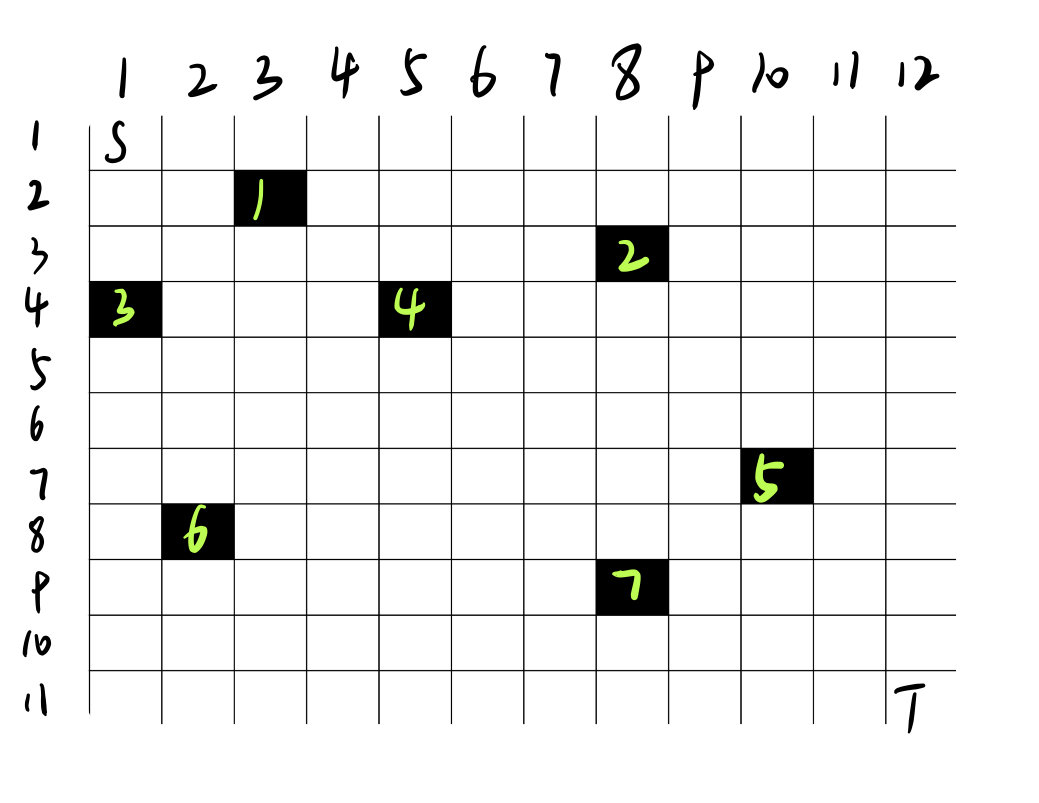
由组合数学知识可知，从S到T的总路径条数为\(C_{H+W-2}^{H-1}\)，只要减去至少经过一个黑格子的路径条数即为答案。

那么如何不重不漏的计数呢？

考虑每条至少经过一个黑格子的路径所包含的第一个黑格子，以4号黑格子(4,5)为例，从S到4号，总路径条数有\(C_{4+5-1-1}^{4-1}\)条，只要排除掉经过3和经过1的路径条数即为从S到4，不经过黑格子的路径数。如何排除？其实我们之前已经算出来了，在算S到4的不经过黑格子路径条数时，已经分别算过了S到3，S到1的不经过黑格子路径条数，只要分别乘上由3到4，由1到4的所有路径数即可。

把所有黑色格子按照行列坐标递增的顺序排序，设\(f[i]\) 为从S到第 \(i\)个格子，途中不经过其他黑色格子的路径数

\[f[i] = C_{x_i-1+y_i-1}^{x_i-1} - \sum_{j=1}^{i-1}f[j]*C_{x_i-x_j+y_i-y_j}^{x_i-x_j},其中x_i\ge x_j,y_i\ge x_j
\]

在求解计数类动态规划时，通常要找一个“基准点",围绕这个基准点构造一个不可划分的”整体",以避免子问题之间的重叠

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
const int N = 2e5+10;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
ll jc[N],inv[N];
int h,w,n;
ll f[2010];
pii a[2010];
ll ksm(ll a,ll b){
    ll res = 1;
    for(;b;b>>=1){
        if(b & 1)res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}
int C(int x,int y){
    return jc[x] * inv[y] %mod * inv[x-y] % mod;
}
int main(){
    jc[0] = 1;inv[0] = 1;
    for(int i=1;i<N;i++)jc[i] = jc[i-1] * i % mod,inv[i] = ksm(jc[i],mod-2);
    scanf("%d%d%d",&h,&w,&n);
    for(int i=1;i<=n;i++)scanf("%d%d",&a[i].fi,&a[i].se);

    sort(a+1,a+1+n);
    a[n+1].fi = h;a[n+1].se = w;

    for(int i=1;i<=n+1;i++){
        int x = a[i].fi,y = a[i].se;
        f[i] = C(x+y-2,x-1);
        for(int j=1;j<i;j++){
            int xj = a[j].fi;
            int yj = a[j].se;
            if(xj > x || yj > y)continue;
            f[i] = (f[i] - (ll)f[j] * C(x-xj+y-yj,x-xj)%mod + mod)%mod;
        }
    }
    printf("%lld\n",f[n+1]%mod);
    return 0;
}