Codeforces Round #631 (Div. 2)

Contest Info

---

Practice Link

Solved	A	B	C	D	E	F
4/6	O	O	Ø

• O 在比赛中通过
• Ø 赛后通过
• ! 尝试了但是失败了
• - 没有尝试

Solutions

---

C.Dreamoon Likes Coloring

题意：

按先后顺序用$m$种颜色涂一个长度为$n$的方块，规定每种颜色必须涂连续的$l_i$块。要求涂色完成后所有格子都有颜色并且存在$m$种颜色，若存在涂色方案则按顺序输出每种颜色涂色的起点，否则输出$-1$

思路：

我们拿到题目首先可以考虑贪心的构造，即尽可能向前涂色，这样就能保证最大程度重叠节省位置。假如在构造过程中超出了方格的范围，显然不存在可行方案，即$i-1+l_i>n$。另外一种极端就是我按顺序不重叠的涂色，假如有空白，这种也不存在可行方案，即$\sum_{i=1}^{m}l_i<n$。

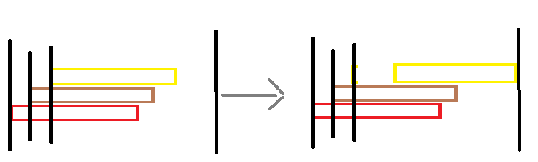
存在涂色方案的情况下，按照上面的构造方式，最后从后向前调整让每个颜色尾部贴到最后，直到把全部覆盖，如图：

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
const int maxn = 1e5+100;
int n, m, l[maxn], p[maxn];
ll sum;
bool fg;
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++){
        scanf("%d", &l[i]);
        sum += l[i];
        if(i-1+l[i]>n) fg = true;
    }
    if(sum<n||fg) return !printf("-1");
    for(int i = 1; i <= m; i++) p[i] = i;
    int len = n;
    for(int i = m; i >= 1; i--){
        if(len-(i-1)>l[i]) p[i] = len-l[i]+1, len -= l[i];
        else break;
    }
    for(int i = 1; i <= m; i++) printf("%d ", p[i]);

我自己重敲代码的时候，曾想用$m-1+l[m]>n$一步到位判断是否存在不合法的情况，仔细想想是不可取的

---

Reference:

https://codeforces.ml/blog/entry/75559

https://www.cnblogs.com/mollnn/p/12630252.html

https://blog.csdn.net/weixin_43769146/article/details/105311326