SLAM中的卡方分布

视觉slam中相邻帧特征点匹配时，动辄上千个特征点，匹配错误的是难免的，而误匹配势必会对位姿精度以及建图精度造成影响，那么如何分辨哪些是误匹配的点对儿呢？如果已知两帧的的单应矩阵，假设单应矩阵是没有误差的，那么两帧中匹配正确的特征点通过单应矩阵是重投影是不应该有误差的或者误差十分小，而误匹配的特征点的重投影误差一定十分显著。那么我们是不是可以设置一个误差门限，从而甄别出这些误匹配点？可是这个误差门限该设置为多少？

假设图像金字塔第n层中一个特征点\(\mathbf{p_c}=\begin{bmatrix}u \\ v\end{bmatrix}\)以及其对应的世界坐标系位置\(\mathbf{p_w}=\begin{bmatrix}x \\ y \\ z\end{bmatrix}\)和转换矩阵\(T_{cw}\)，将空间点重投影到图像中为\(\mathbf{p_c'}=\begin{bmatrix}u' \\ v'\end{bmatrix}\)。那么x轴的重投影误差\(e_x=u-u'\)，假设变换矩阵没有误差，实际中由于不同时刻拍摄以及成像原因，会给重投影误差带来噪声，不妨假设\(e_x\sim N(0,\sigma_x^2)\)，同理假设\(e_y\sim N(0,\sigma_y^2)\)，并假设噪声方差\(\sigma_x^2=\sigma_y^2=(s^n\times n\_pixels)^2\)，\(n\_pixels\)为噪声所带来的的像素误差数，这里取值1，s为图像金字塔的缩放因子，通常取1.2，有\(\sigma_x^2=\sigma_y^2=(s^n)^2\)显然方差与特征点所处的层数有关。这里面表达了特征点所处的金字塔层数越高，重投影误差的方差就越大。因此有\(\frac {1}{s^n}e_x\sim N(0,1),\frac {1}{s^n}e_y\sim N(0,1)\)。

卡方分布

若k个随机变量\(Z_1,Z_2,...,Z_k\)是相互独立，符合标准正态分布的随机变量（数学期望为0、方差为1），则随机变量Z的平方和\(X=\sum_{i-1}^{k}Z_i^2\)被称为服从自由度为 k 的卡方分布，记作\(X\sim\chi^2(k)\)。

令\(Z_1=\frac {1}{s^n}e_x,Z_2=\frac {1}{s^n}e_y,X=Z_1^2+Z_2^2\)，根据卡方分布的定义，\(X\sim\chi^2(2)\)，即2自由度的卡方分布。对于双目匹配到的特征点在右图中的x坐标为\(u_r'\)，重投影后计算得到特征点左图的x坐标\(u_l\),根据\(视差d=\frac {基线b*f_x}{深度}\)，可以计算出视差从而得到重投影后右图中特征点x坐标\(u_r=u_l-d\)，得\(e_r=u_r'-u_r\)。同理\(\frac {1}{s^n}e_r\sim N(0,1)\)，可构成卡方分布的另一个自由度，而\(X\)的物理意义就是各项误差的平方和。

下图为不同自由度卡方分布的概率密度函数和累积分布函数，分布函数记为\(F(X\leqslant x)=\alpha\)，\(\alpha\)就是一个概率值，表示如果\(X\)服从卡方分布，那么\(X\)就有\(\alpha\)的概率值在\([0,x]\)中。如果已知\(\alpha\)的值，通过查表的方法我们可以找到对应的\(x\)值。比如2自由度的卡方分布，\(X\in [0,5.99]\)时，我们有95%的把握认为\(X\)是服从该分布的，以此将\(X>5.99\)的时候将该特征点排除。

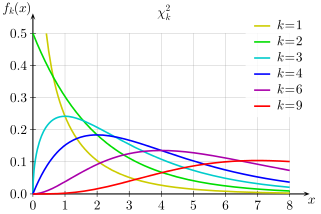
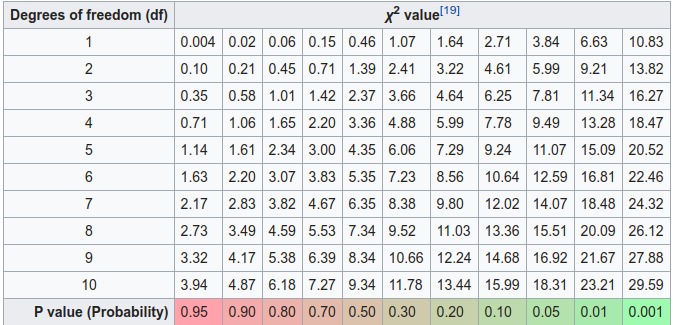
下图为卡方阈值与对应P值的查找表，可以简单的认为\(P值=1-\alpha\)。具体解释可以参考如何理解假设检验、P值？。

实际代码

// openvslam/module/two_view_triangulator.cc:95

// chi-squared values for p=5%

// (n=2)

constexpr float chi_sq_2D = 5.99146;

// (n=3)

constexpr float chi_sq_3D = 7.81473;

Vec2_t reproj_in_cur;

float x_right_in_cur;

camera->reproject_to_image(rot_cw, trans_cw, pos_w, reproj_in_cur, x_right_in_cur);

if (is_stereo) {

    const Vec2_t reproj_err = reproj_in_cur - keypt;

    const auto reproj_err_x_right = x_right_in_cur - x_right;

    if ((chi_sq_3D * sigma_sq) < (reproj_err.squaredNorm() + reproj_err_x_right * reproj_err_x_right)) {

        return false;

    }

}

else {

    const Vec2_t reproj_err = reproj_in_cur - keypt;

    if ((chi_sq_2D * sigma_sq) < reproj_err.squaredNorm()) {

        return false;

    }

}

上面的代码reproject_to_image就是将3D点重投影回图像中，reproj_err就是上文中的\(\begin{bmatrix}e_x \\ e_y\end{bmatrix}，sigma\_sq=(s^n)^2\)，reproj_err.squaredNorm()/sigma_sq就是\((\frac {1}{s^n})^2(e_x^2+e_y^2)=Z_1^2+Z_2^2=X\sim\chi^2(k)\)。

参考