在Spring Security框架下JWT的实现细节原理

一、回顾JWT的授权及鉴权流程

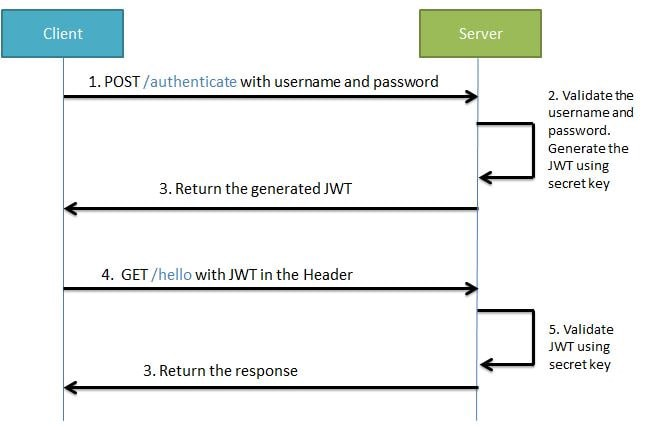
在笔者的上一篇文章中，已经为大家介绍了JWT以及其结构及使用方法。其授权与鉴权流程浓缩为以下两句话

• 授权：使用可信用户信息（用户名密码、短信登录）换取带有签名的JWT令牌
• 鉴权：解签JWT令牌，校验用户权限。具有某个接口访问权限，开放该接口访问。

二、Spring Security授权细节说明

我相信大家都能理解上面的授权与鉴权的整体流程，但是具体到使用Spring Security 如何实现授权，其中细节及原理还是需要单独提出来说明一下。

2.1.授权流程细节：

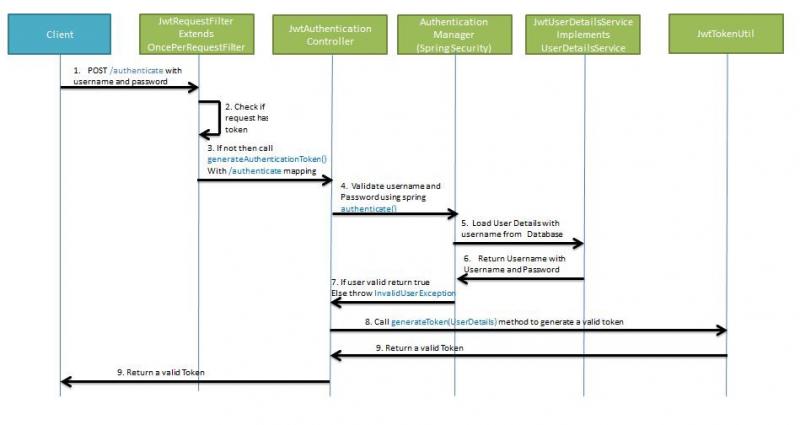
• 当客户端发送“/authentication”请求的时候，实际上是请求JwtAuthenticationController。该Controller的功能是：一是用户登录功能的实现，二是如果登录成功，生成JWT令牌。在使用JWT的情况下，这个类需要我们自己来实现。
• 具体到用户登录，就需要结合Spring Security实现。通过向Spring Security提供的AuthenticationManager的authenticate()方法传递用户名密码，由spring Security帮我们实现用户登录认证功能。
• 如果登陆成功，我们就要为该用户生成JWT令牌了。通常此时我们需要使用UserDetailsService的loadUserByUsername方法加载用户信息，然后根据信息生成JWT令牌，JWT令牌生成之后返回给客户端。（spring security的UserDetailsService的功能以及实现，笔者之前的文章已经讲过）
• 另外，我们需要写一个工具类JwtTokenUtil，该工具类的主要功能就是根据用户信息生成JWT，解签JWT获取用户信息，校验令牌是否过期，刷新令牌等。

2.2.接口鉴权细节：

当客户端获取到JWT之后，他就可以使用JWT请求接口资源服务了。大家可以看到在“授权流程细节”的时序图中，有一个Filter过滤器我们没有讲到，其实它和授权认证的流程关系不大，它是用来进行接口鉴权的。因为授权认证就只有一个接口即可，但是服务资源接口却有很多，所以我们不可能在每一个Controller方法中都进行鉴权，所以在到达Controller之前通过Filter过滤器进行JWT解签和权限校验。

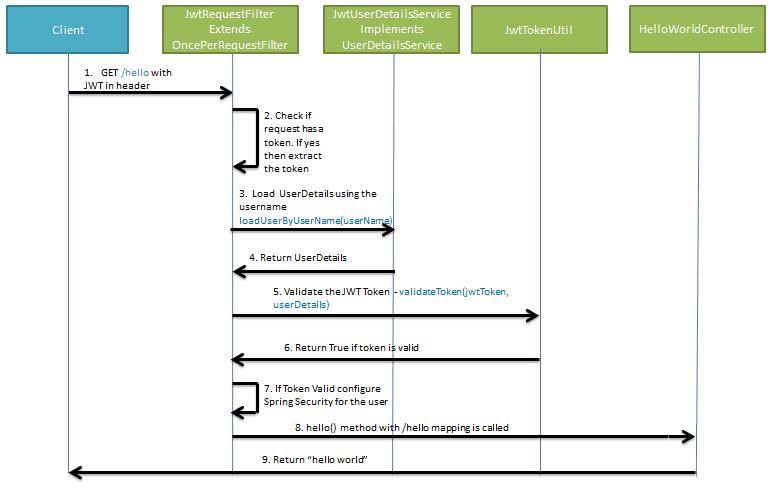
假如我们有一个接口资源“/hello”定义在HelloWorldcontroller中，鉴权流程是如何进行的？请结合上图进行理解：

• 当客户端请求“/hello”资源的时候，他应该在HTTP请求的Header带上JWT字符串。Header的名称前后端服务自己定义，但是要统一。
• 服务端需要自定义JwtRequestFilter，拦截HTTP请求，并判断请求Header中是否有JWT令牌。如果没有，就执行后续的过滤器。因为Spring Security是有完成的鉴权体系的，你没赋权该请求就是非法的，后续的过滤器链会将该请求拦截，最终返回无权限访问的结果。
• 如果在HTTP中解析到JWT令牌，就调用JwtTokenUtil对令牌的有效期及合法性进行判定。如果是伪造的或者过期的，同样返回并执行spring security后续的过滤器链。
• 如果JWT令牌在有效期内并且校验通过，我们仍然要通过UserDetailsService加载该用户的权限信息，并将这些信息交给Spring Security。只有这样，该请求才能顺利通过Spring Security一系列过滤器的关卡，顺利到达HelloWorldcontroller并访问“/hello”接口。

三、其他的细节问题

• 一旦发现用户的JWT令牌被劫持，或者被个人泄露该怎么办？JWT令牌有一个缺点就是一旦发放，在有效期内都是可用的，那怎么回收令牌？我们可以通过设置黑名单ip、用户，或者为每一个用户JWT令牌使用一个secret密钥，可以通过修改secret密钥让该用户的JWT令牌失效。

• 如何刷新令牌？为了提高安全性，我们的令牌有效期通常时间不会太长。那么，我们不希望用户正在使用app的时候令牌过期了，用户必须重新登陆，很影响用户体验。这怎么办？这就需要在客户端根据业务选择合适的时机或者定时的刷新JWT令牌。所谓的刷新令牌就是用有效期内，用旧的合法的JWT换取新的JWT。

  期待您的关注

• 向您推荐博主的系列文档：《手摸手教您学习SpringBoot系列-16章97节》

• 本文转载注明出处（必须带连接，不能只转文字）：字母哥博客。