强连通分量-----Kosaraju

芝士：

有向图强连通分量在有向图G中，如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量。

如图中1,2,3,4是一个强连通分量。

Kosaraju算法：

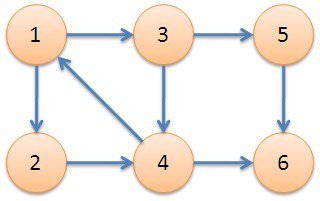
如果这是一个无向图，那么从一个节点出发，深搜得到的所有节点都是连通的。

但这是一个有向图，起始节点的不同会导致结果的不同，举个栗子，从5搜可以搜到6，但是从6搜不能搜到5。

这说明需要按照一个特定的顺序深搜。假设1,2,3,4是强连通分量a，5,6分别是强连通分量b,c。a可以搜到b,c,但b,c不能搜到a，由于我们不希望搜到不属于同一个强连通分量的点，所以会先搜b,c，再搜a。

那么这个顺序就是被指向的强连通分量要在指向的强连通分量之前被搜到，即被指向的强连通分量中的至少一个点在指向的强连通分量的任意一个点之前被搜到。

为了得到这个顺序，聪明的Kosaraju想到了一个方法：新建原图G的逆图G^T(其定义为GT=(V,ET)，ET={(u,v):(v,u)∈E}}),按照节点编号顺序在G^T上深搜，每搜到一个节点，先把这个节点所能到达的所有未被访问过的节点加入栈中，再把自己加入栈中，然后按照从栈顶到栈底的顺序深搜，这样保证了在原图G中能到达我的点，都在我之后被搜到；

最后原图中强连通分量的个数就等于深搜的次数，每一次深搜到达的未被访问过的节点属于一个强连通分量(可以用一个数组记录一下)；

Tarjan算法

从一个点开始遍历图，会得到一棵有向树，当一个点有连向其祖先的边(回边)时，就会形成环，而连另一棵子树的边则不会。

每个点有一个时间戳t[i]，和一个top[i]表示能反到的最高的点的时间戳，vis[i]表示这个点是否在栈中。

从一个点开始dfs，遍历子节点并把它们加入栈中，如果找到了被遍历且在栈中的点，修改自己的top为那个在栈中的点的时间戳。遍历完所有子节点后，尝试用子节点的top更新自己的top，如果自己的top等于自己的t，那么自己是所在联通块里最高的点，这是从栈中弹出元素一直到弹出自己就找到了自己所在的联通块。

如果图不连通，需要从多个点开始dfs。

模板：

/*
约翰的N (2 <= N <= 10,000)只奶牛非常兴奋，因为这是舞会之夜！她们穿上礼服和新鞋子，别上鲜花，她们要表演圆舞.
只有奶牛才能表演这种圆舞.圆舞需要一些绳索和一个圆形的水池.奶牛们围在池边站好， 顺时针顺序由1到N编号.每只奶牛都面对水池，这样她就能看到其他的每一只奶牛.
为了跳这种圆舞，她们找了 M(2<M< 50000)条绳索.若干只奶牛的蹄上握着绳索的一端， 绳索沿顺时针方绕过水池，另一端则捆在另一些奶牛身上.这样，一些奶牛就可以牵引另一些奶 牛.
有的奶牛可能握有很多绳索，也有的奶牛可能一条绳索都没有.对于一只奶牛，比如说贝茜，她的圆舞跳得是否成功，可以这样检验：沿着她牵引的绳索， 找到她牵引的奶牛，再沿着这只奶牛
牵引的绳索，又找到一只被牵引的奶牛，如此下去，若最终 能回到贝茜，则她的圆舞跳得成功，因为这一个环上的奶牛可以逆时针牵引而跳起旋转的圆舞. 如果这样的检验无法完成，那她的
圆舞是不成功的.如果两只成功跳圆舞的奶牛有绳索相连，那她们可以同属一个组合.给出每一条绳索的描述，请找出，成功跳了圆舞的奶牛有多少个组合？
输入n,m，接下来m行
*/
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define nn 10010
#define mm 100010
using namespace std;
int e=0,l=0,ee=0,cir;
int nx[mm],fi[nn],too[mm];
int fir[nn],nxt[mm],to[mm],li[nn];
bool vis[nn];
void add(int u,int v)
{
    nxt[++e]=fir[u];fir[u]=e;to[e]=v;
}
void add2(int u,int v)
{
    nx[++ee]=fi[u];fi[u]=e;too[e]=v;
}
void dfs(int s)
{
    vis[s]=1;
    for(int i=fi[s];i;i=nx[i])
    {
        if(!vis[too[i]])
          dfs(too[i]);
    }
    li[++l]=s;
}
void dfs2(int s)
{
    vis[s]=1;cir++;
    for(int i=fir[s];i;i=nxt[i])
    {
        if(!vis[to[i]])
          dfs2(to[i]);         //写成了dfs
    }
}
int main()
{
    int n,m,u,v,ma=-1,sum=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
        add2(v,u);
    }
    for(int i=1;i<=n;i++)
      if(!vis[i])
        dfs(i);
    fill(vis,vis+n+1,0);
    for(int i=l;i>=1;i--)
      if(!vis[li[i]])                 //写成了vis[i]
      {
          cir=0;
          dfs2(li[i]);
          if(cir>=2) sum++;
      }
    printf("%d",sum);
    return 0;
}

/*洛谷3387
给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。
*/
#include<algorithm>
#include<iostream>
#include<cstring>         //
#include<cstdlib>
#include<cstdio>
#include<queue>
#define nn 10010
#define mm 100010
using namespace std;
int e=0,ee=0,time=0,la=0,var=0,head=1,tail=0;
int fir[nn],fi[nn],nxt[mm],nx[mm],to[mm],too[mm],q[nn],t[nn],top[nn],stack[nn],w[nn],d[nn],be[nn],dis[nn],in[nn];
bool vis[nn];
int read()
{
    int ans=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {ans=ans*10+ch-'0';ch=getchar();}
    return ans*f;
}
void add(int u,int v)
{
    nxt[++e]=fir[u];fir[u]=e;to[e]=v;
}
void ad(int u,int v)
{
    nx[++ee]=fi[u];fi[u]=ee;too[ee]=v;
}
void tarjan(int s)
{
    t[s]=top[s]=++time;
    stack[++la]=s;
    vis[s]=1;
    for(int i=fir[s];i;i=nxt[i])
      if(!t[to[i]])
      {
          tarjan(to[i]);
          top[s]=min(top[s],top[to[i]]);
      }
      else if(vis[to[i]])
        top[s]=min(top[s],t[to[i]]);         //
    if(t[s]!=top[s])          //最高的点才找出这个联通分量
      return;
    var++;
    do
    {
        w[var]+=d[stack[la]];
        be[stack[la]]=var;
        vis[stack[la]]=0;
        la--;
    }while(stack[la+1]!=s);           //la+1
}
int dp()
{
    int o,ma=-1;
    while(head<=tail)
    {
        o=q[head++];
        if(dis[o]>ma)
          ma=dis[o];
        for(int i=fi[o];i;i=nx[i])
        {
            in[too[i]]--;
            if(dis[too[i]]<dis[o]+w[too[i]])         //w写成了d
              dis[too[i]]=dis[o]+w[too[i]];
            if(!in[too[i]])
              q[++tail]=too[i];
        }
    }
    for(int i=1;i<=var;i++)
      if(w[var]>ma)
        ma=w[var];
    return ma;
}
int main()
{
    int n,m,u,v;
    n=read();m=read();
    for(int i=1;i<=n;i++)
      d[i]=read();
     for(int i=1;i<=m;i++)
     {
         u=read();v=read();
         add(u,v);
     }
     for(int i=1;i<=n;i++)
       if(!t[i])
         tarjan(i);
     for(int i=1;i<=n;i++)
       for(int j=fir[i];j;j=nxt[j])
         if(be[i]!=be[to[j]])
         {
             ad(be[i],be[to[j]]);
             in[be[to[j]]]++;
         }
     for(int i=1;i<=var;i++)
       if(!in[i])
       {
           dis[i]=w[i];
           q[++tail]=i;
       }
    printf("%d",dp());
}
/*
5 6
2 5 4 1 3
1 2
2 3
2 4
4 5
5 3
4 1
*/