GYM100741 A Queries

A. Queries

time limit per test

0.25 s

memory limit per test

64 MB

input

standard input

output

standard output

Mathematicians are interesting (sometimes, I would say, even crazy) people. For example, my friend, a mathematician, thinks that it is very fun to play with a sequence of integer numbers. He writes the sequence in a row. If he wants he increases one number of the sequence, sometimes it is more interesting to decrease it (do you know why?..) And he likes to add the numbers in the interval [l;r]. But showing that he is really cool he adds only numbers which are equal some mod (modulo m).

Guess what he asked me, when he knew that I am a programmer? Yep, indeed, he asked me to write a program which could process these queries (n is the length of the sequence):

• + p r It increases the number with index p by r. (, )

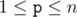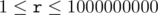  You have to output the number after the increase.

• - p r It decreases the number with index p by r. (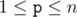, 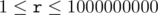) You must not decrease the number if it would become negative.

  You have to output the number after the decrease.

• s l r mod You have to output the sum of numbers in the interval 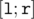which are equal mod (modulo m). () ()

Input

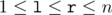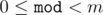The first line of each test case contains the number of elements of the sequence n and the number m. (1 ≤ n ≤ 10000) (1 ≤ m ≤ 10)

The second line contains n initial numbers of the sequence. (0 ≤ number ≤ 1000000000)

The third line of each test case contains the number of queries q (1 ≤ q ≤ 10000).

The following q lines contains the queries (one query per line).

Output

Output q lines - the answers to the queries.

Examples

Input

3 4
1 2 3
3
s 1 3 2
+ 2 1
- 1 2

Output

2
3
1

【题解】

m棵线段树即可

树状数组就够了，但是我就是想写线段树练一练怎么了（唔）

 #include <iostream>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <cstdio>
 #define max(a, b) ((a) > (b) ? (a) : (b))
 #define min(a, b) ((a) < (b) ? (a) : (b))

 inline void read(long long &x)
 {
     x = ;char ch = getchar(), c = ch;
     while(ch < '' || ch > '')c = ch, ch = getchar();
     while(ch <= '' && ch >= '')x = x *  + ch - '', ch = getchar();
     if(c == '-')x = - x;
 }

 const long long INF = 0x3f3f3f3f;
 const long long MAXN =  + ;

 long long n,m,num[MAXN],sum[][MAXN];

 void build(long long o = , long long l = , long long r = n)
 {
     if(l == r)
     {
         sum[num[l]%m][o] += num[l];
         return;
     }
     long long mid = (l + r) >> ;
     build(o << , l, mid);
     build(o <<  | , mid + , r);
     for(register long long i = ;i <= ;++ i)
         sum[i][o] = sum[i][o << ] + sum[i][o <<  | ];
     return;
 }

 void modify(long long p, long long shu, long long x, long long o = , long long l = , long long r = n)
 {
     if(l == p && l == r)
     {
         sum[shu % m][o] += x * shu;
         return;
     }
     long long mid = (l + r) >> ;
     if(mid >= p) modify(p, shu, x, o << , l, mid);
     else modify(p, shu, x, o <<  | , mid + , r);
     sum[shu % m][o] = sum[shu % m][o << ] + sum[shu % m][o <<  | ];
 }

 long long ask(long long ll, long long rr, long long rk, long long o = , long long l = , long long r = n)
 {
     if(ll <= l && rr >= r) return sum[rk][o];
     long long mid = (l + r) >> ;
     long long ans = ;
     if(mid >= ll) ans += ask(ll, rr, rk, o << , l, mid);
     if(mid < rr)  ans += ask(ll, rr, rk, o <<  | , mid + , r);
     return ans;
 }

 long long q;
 char c;

 int main()
 {
     read(n), read(m);
     for(register long long i = ;i <= n;++ i)
         read(num[i]);
     build();
     read(q);
     for(register long long i = ;i <= q;++ i)
     {
         long long tmp1,tmp2,tmp3;
         scanf("%s", &c);
         if(c == 's')
         {
             read(tmp1), read(tmp2), read(tmp3);
             printf("%I64d\n", ask(tmp1, tmp2, tmp3));
         }
         else if(c == '+')
         {
             read(tmp1), read(tmp2);
             modify(tmp1, num[tmp1], -);
             num[tmp1] += tmp2;
             modify(tmp1, num[tmp1], );
             printf("%I64d\n", num[tmp1]);
         }
         else
         {
             read(tmp1), read(tmp2);
             modify(tmp1, num[tmp1], -);
             if(num[tmp1] - tmp2 >= ) num[tmp1] -= tmp2;
             modify(tmp1, num[tmp1], );
             printf("%I64d\n", num[tmp1]);
         }
     }
     return ;
 } 

GYM100741 A