hdu多校第八场 1009 （hdu6665） Calabash and Landlord 计算几何/dfs

题意：

给定两个矩形，输出这两个矩形把平面分成了多少块。

题解：

本来是道计算几何的大讨论，被我生生写成了bfs。

离散化边，注意不重合的边中间要空出来一格，四周也要空出来一圈，然后暴力bfs计算一共有几块即可。

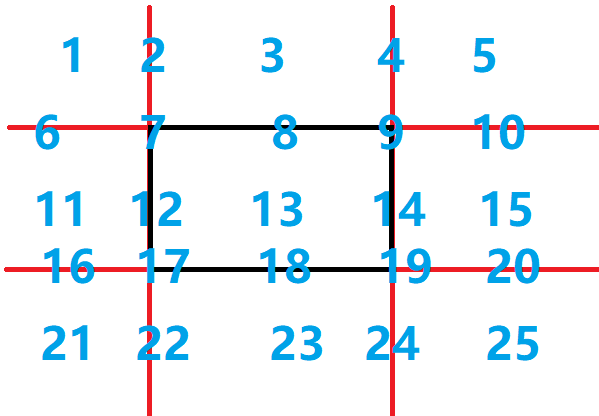
不这么暴力的方法倒也不是没有，观察下图，点与长方形的关系存在如下25种，那么两点确定一个长方形，两个长方形的关系则共有625种

至于这个表怎么打，好像还得借助一下bfs。

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
int mapp[][];
int x[],y[];
const int changex[]={,,,-};
const int changey[]={,-,,};
void lsh(int *a){
    int b[];
    bool flag[]={};
    b[]=a[];b[]=a[];b[]=a[];b[]=a[];
    sort(b+,b+);
    int l=unique(b+,b+)-b-;
    for(int i=;i<=l;i++){
        for(int j=;j<=;j++){
            if(a[j]==b[i] && flag[j]==){
                a[j]=*i;
                flag[j]=;
            }
        }
    }
    return ;
}
int solve(){
    int ans=;
    memset(mapp,,sizeof mapp);
//    printf("a:%d %d %d %d\n",x[1],y[1],x[2],y[2]);
//    printf("b:%d %d %d %d\n",x[3],y[3],x[4],y[4]);
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            if((i==x[] || i==x[]) && j>=y[] && j<=y[]){
                mapp[i][j]=-;
            }
            if((j==y[] || j==y[]) && i>=x[] && i<=x[]){
                mapp[i][j]=-;
            }
            if((i==x[] || i==x[]) && j>=y[] && j<=y[]){
                mapp[i][j]=-;
            }
            if((j==y[] || j==y[]) && i>=x[] && i<=x[]){
                mapp[i][j]=-;
            }
        }
    }

//    for(int i=1;i<=10;i++){
//            for(int j=1;j<=10;j++){
//                printf("%c ",mapp[i][j]==-1?'*':mapp[i][j]+'0');
//            }
//            printf("\n");
//        }
//
    queue<int> qx,qy;
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            if(mapp[i][j]==){
                ans++;
                mapp[i][j]=ans;
                qx.push(i);
                qy.push(j);
            }
            while(!qx.empty()){
                int xx=qx.front();
                int yy=qy.front();
                qx.pop();qy.pop();
//                printf("%d %d:",xx,yy);
                for(int k=;k<;k++){
                    int xxx=xx+changex[k];
                    int yyy=yy+changey[k];
//                    printf("%d %d ",xxx,yyy);
                    if(xxx>= && xxx<= && yyy>= && yyy<= && mapp[xxx][yyy]==){
                        qx.push(xxx);
                        qy.push(yyy);
                        mapp[xxx][yyy]=ans;
                    }
                }
//                printf("\n");
            }
//            for(int i=1;i<=10;i++){
//            for(int j=1;j<=10;j++){
//                printf("%c ",mapp[i][j]==-1?'*':mapp[i][j]+'0');
//            }
//            printf("\n");
//        }
        }
    }
    return ans;
}
int main(){

    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d %d %d %d",&x[],&y[],&x[],&y[]);
        scanf("%d %d %d %d",&x[],&y[],&x[],&y[]);
        lsh(x);lsh(y);
        printf("%d\n",solve());
//        for(int i=1;i<=10;i++){
//            for(int j=1;j<=10;j++){
//                printf("%c ",mapp[i][j]==-1?'*':mapp[i][j]+'0');
//            }
//            printf("\n");
//        }
    }
}