HNOI 2019 多边形

HNOI 2019 多边形

题意

小 R 与小 W 在玩游戏。

他们有一个边数为\(n\)的凸多边形，其顶点沿逆时针方向标号依次为\(1,2,3...n\)。最开始凸多边形中有\(n\)条线段，即多边形的\(n\)条边。这里我们用一个有序数对 \((a,b)\)（其中\(a<b\)）来表示一条端点分别为顶点\(a,b\)的线段。

在游戏开始之前，小 W 会进行一些操作。每次操作时，他会选中多边形的两个互异顶点，给它们之间连一条线段，并且所连的线段不会与已存的线段重合、相交（只拥有一个公共端点不算作相交）。他会不断重复这个过程，直到无法继续连线，这样得到了状态\(S_0\)。

小 W 定义了一种「旋转」操作：对于当前状态，选定\(1\le a<b<c<d\le n\)共\(4\)个顶点 ，它们两两之间共有\(5\)条线段—— \((a,b),(b,c),(c,d),(a,d),(a,c)\)，然后删去线段\((a,c)\)，并连上线段\((b,d)\) 。那么用有序数对\((a,b)\)即可唯一表示该次「旋转」。我们称这次旋转为\((a,c)\)「旋转」。显然每次进行完“旋转”操作后多边形中依然不存在相交的线段。

当小 W 将一个状态作为游戏初始状态展示给小 R 后，游戏开始。游戏过程中，小 R 每次可以对当前的状态进行「旋转」。在进行有限次「旋转」之后，小 R 一定会得到一个状态，此时无法继续进行「旋转」操作，游戏结束。那么将每一次「旋转」所对应的有序数对按操作顺序写下，得到的序列即为该轮游戏的操作方案。

为了加大难度，小W以\(S_0\)为基础，产生了\(m\)个新状态。其中第\(i\)个状态 为对\(S_0\)进行一次「旋转」操作后得到的状态。你需要帮助小R求出分别以\(S_i\)作为游戏初始状态时，小R完成游戏所用的最少「旋转」次数，并根据小W的心情，有时还需求出旋转次数最少的不同操作方案数。由于方案数可能很大，输出时请对\(10^9+7\)取模。

思路

不难发现，边的变化具有方向性，即一条边总是往标号变大的方向变化。

那么，就可以猜测，最终状态为从\(n\)出发的\(n-3\)条线段。

仔细思索，不难证明这个结论是正确的。

再观察样例，猜测最小步数为不与\(n\)相连的边的数目。

这个结论好像也是对的。

所以每次操作必须把一个与\(n\)不相连的边变为与\(n\)相连的边。

由于必须保证不相交，所以这些边的操作有些先后顺序。

他形成了一颗二叉森林的结构。

只考虑一颗树，他的方案数是多少？

\[\prod_{x}{{siz_{ls_x}+siz_{rs_x}}\choose{siz_{ls_x}}}
\]

它的组合意义是，枚举每个\(x\)的左子树和右子树的次序。

如果把所有树都考虑进去，只需要再枚举一下树之间的次序就可以了。

经过长期的摸索，发现进行一次旋转会有这样的改变。

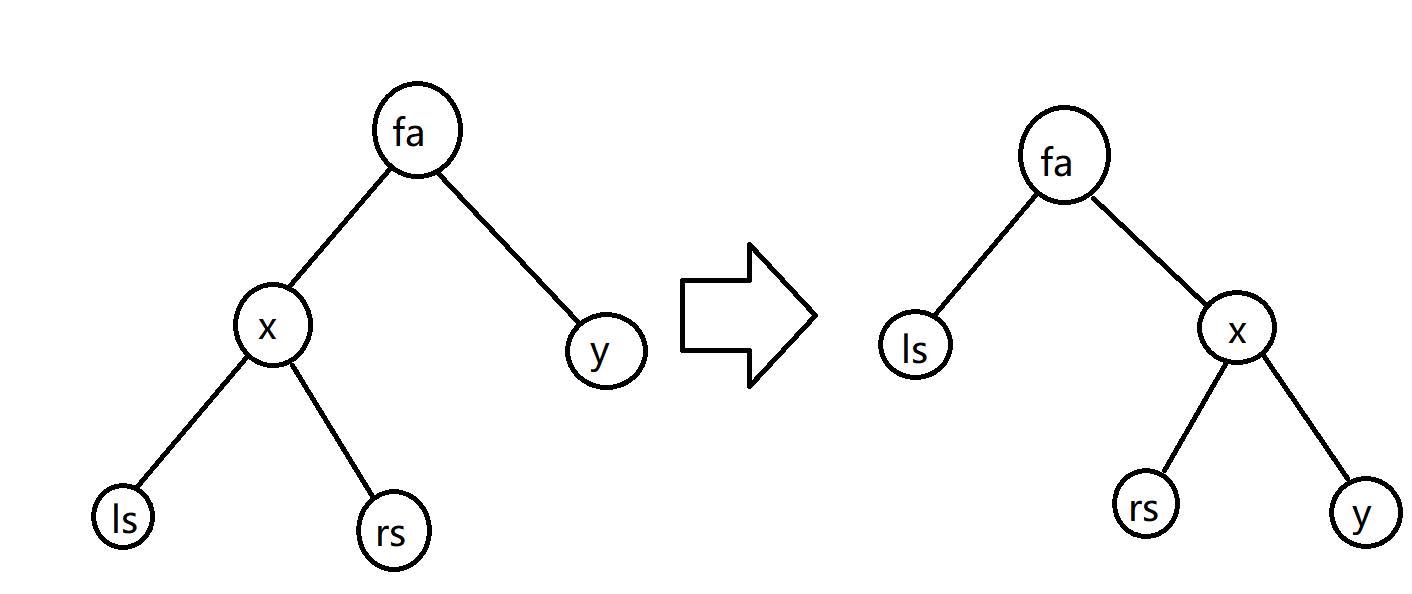
这是改变\(x\)这条边。答案并不会有很大的变动。

以上。

代码

#include<bits/stdc++.h>
#define pii pair<int,int>
#define mkp(x,y) make_pair(x,y)
using namespace std;
const int sz=1e5+7;
const int mod=1e9+7;
int w;
int n,m;
int r[sz];
int ans,tot;
int Ans,Tot;
int u,v,cnt;
int siz[sz];
int ls[sz],rs[sz],f[sz];
int fac[sz],ifac[sz],inv[sz];
map<pii,int>mp;
struct Edge{
	int u,v;
}e[sz];
bool cmp1(Edge p1,Edge p2){
	if(p1.u!=p2.u) return p1.u<p2.u;
	return p1.v>p2.v;
}
bool cmp2(Edge p1,Edge p2){
	if(p1.v!=p2.v) return p1.v>p2.v;
	return p1.u<p2.u;
}
void init(){
	fac[0]=ifac[0]=1;
	fac[1]=ifac[1]=inv[1]=1;
	for(int i=2;i<sz;i++){
		inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
		fac[i]=1ll*i*fac[i-1]%mod;
		ifac[i]=1ll*inv[i]*ifac[i-1]%mod;
	}
}
int C(int n,int m){
	return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
int iC(int n,int m){
	return 1ll*ifac[n]*fac[m]%mod*fac[n-m]%mod;
}
void dfs(int x){
	siz[x]=1;
	if(ls[x]){
		dfs(ls[x]);
		siz[x]+=siz[ls[x]];
	}
	if(rs[x]){
		dfs(rs[x]);
		siz[x]+=siz[rs[x]];
	}
	ans=1ll*ans*C(siz[ls[x]]+siz[rs[x]],siz[ls[x]])%mod;
}
int main(){
	init();
	scanf("%d",&w);
	scanf("%d",&n);
	for(int i=1;i<=n-3;i++){
		scanf("%d%d",&u,&v);
		if(u>v) swap(u,v);
		e[i]=(Edge){u,v};
		mp[mkp(u,v)]=i;
	}
	sort(e+1,e+n-2,cmp1);
	for(int i=1;i<=n-3;i++){
		int nu=e[i].u,nv=e[i].v;
		int lu=e[i-1].u,lv=e[i-1].v;
		if(nv==n) { r[mp[mkp(nu,nv)]]=1;continue;}
		if(lv==n) continue;
		if(nu==lu){
			ls[mp[mkp(lu,lv)]]=mp[mkp(nu,nv)];
			f[mp[mkp(nu,nv)]]=mp[mkp(lu,lv)];
			r[mp[mkp(nu,nv)]]=1;
		}
	}
	sort(e+1,e+n-2,cmp2);
	for(int i=1;i<=n-3;i++){
		int nu=e[i].u,nv=e[i].v;
		int lu=e[i-1].u,lv=e[i-1].v;
		if(nv==n) { r[mp[mkp(nu,nv)]]=1; continue; }
		if(lv==n) continue;
		if(nv==lv){
			rs[mp[mkp(lu,lv)]]=mp[mkp(nu,nv)];
			f[mp[mkp(nu,nv)]]=mp[mkp(lu,lv)];
			r[mp[mkp(nu,nv)]]=1;
		}
	}
	ans=1;
	for(int i=1;i<=n-3;i++){
		if(r[i]) continue;
		dfs(i);
		ans=1ll*ans*ifac[siz[i]]%mod;
		tot+=siz[i];
	}
	ans=1ll*ans*fac[tot]%mod;
	printf("%d ",tot);
	if(w) printf("%d ",ans);
	printf("\n");
	scanf("%d",&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&u,&v);
		if(u>v) swap(u,v);
		int num=mp[mkp(u,v)];
		if(!f[num]){
			Tot=tot-1;
			Ans=ans;
			Ans=1ll*Ans*ifac[tot]%mod*fac[Tot]%mod;
			Ans=1ll*Ans*fac[siz[num]]%mod*ifac[siz[num]-1]%mod;
			printf("%d ",Tot);
			if(w) printf("%d ",Ans);
		}
		else{
			Tot=tot;
			Ans=ans;
			Ans=1ll*Ans*iC(siz[f[num]]-1,siz[num])%mod;
			Ans=1ll*Ans*C(siz[f[num]]-1,siz[ls[num]])%mod;
			Ans=1ll*Ans*iC(siz[num]-1,siz[ls[num]])%mod;
			Ans=1ll*Ans*C(siz[rs[f[num]]]+siz[rs[num]],siz[rs[num]])%mod;
			printf("%d ",Tot);
			if(w) printf("%d ",Ans);
		}
		printf("\n");
	}
}