PCA技术的自我理解（催眠

Principal component analysis(PCA)

中文就是主成成分分析。在学数学建模的时候将这分为了评价类的方法（我实在是很难看出来，在机器学习中是属于无监督学习降维方法的一种线性降维方法。

举一个最简单的栗子（下图，二维的数据降到一维，就得找到一条直线将所有的点都投影到该直线上，这条直线需要满足的条件就是投影在这条直线上的所有点的方差最大，减少信息的损失。



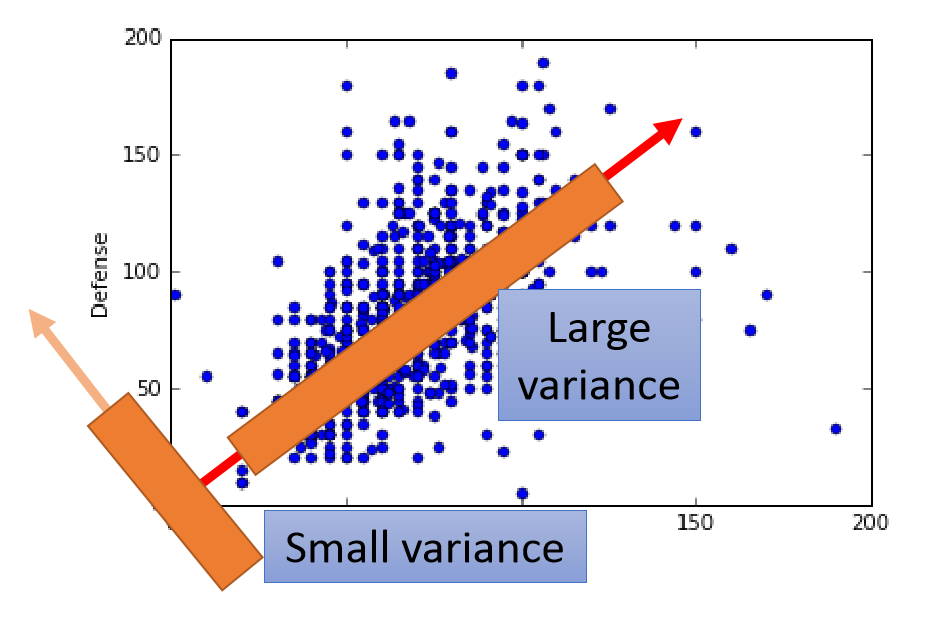
PCA主要用于当数据的维度过高或者不同维度的数据之间存在相关的关系，造成了机器学习性能的下降的问题。这个时候PCA就是要将高维特征转化为独立性较高的低维特征，降低特征之间的相关性。

Math of warning!

\(X_{nxm}\):n维特征的数据，\(Z_{kxm}\):k维特征的数据，PCA技术就是要找到一组\(W_{kxn}\)使得\(Z=W\cdot X\)，同时\(Maximize(\sum_i^kVar(Z_i))\),\(Z_i\)表示第i-D下的投影。

• 第一步 将X降到\(Z_1,Z_2\)上
  
  \(Z_1=W_1\cdot X\)
  
  \(Var(Z_1)=\frac{1}{m}\sum_{j=1}^m(Z_{1j}-\overline{Z_1})^2\),\(|W_1|=1\)投影但是不影响大小
  
  \(Z_2=W_2\cdot X\)
  
  \(Var(Z_2)=\frac{1}{m}\sum_{j=1}^m(Z_{2j}-\overline{Z_2})^2\),\(|W_2|=1\)投影但是不影响大小,但是为了是方差最大或者说使特征之间的相关性最低，\(W_1\cdot W_2=0\)
  
  PS：如果不加这个条件的话\(W_1==W_2\)

• 第二步 求解\(Var(Z_1),Var(Z_2)\)
  
  
  
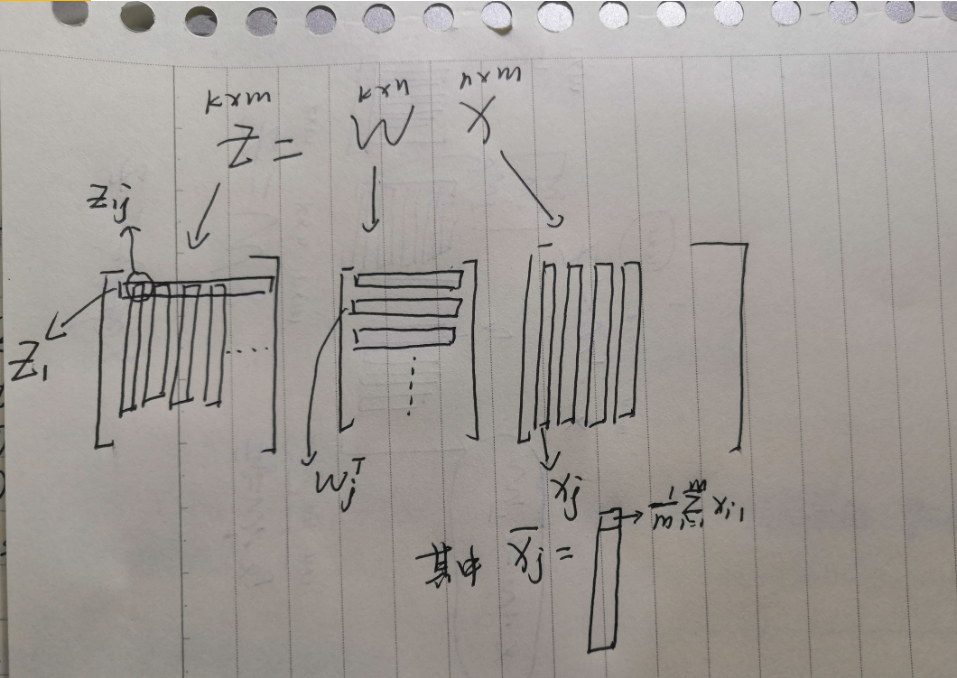
  PS:注意这里加\(\cdot\)是向量积，不加的是矩阵乘法(坑

• \(Z_{1j}=W_1\cdot X_j,\overline{Z_1}=\frac{1}{m}\sum_{j=1}^mZ_{1j}=\frac{1}{m}\sum_{j=1}^mW_1\cdot X_j=W_1\cdot \overline{X_j}\)

• \(Var(Z_1)=\frac{1}{m}\sum_{j=1}^m(W_1\cdot X_j-W_1\cdot \overline{X_j})^2=\frac{1}{m}\sum_{j=1}^m[W_1\cdot (X_j-\overline{X_j})]^2=W_1^T[\frac{1}{m}\sum_{j=1}^m(X_j-\overline{X_j})(X_j-\overline{X_j})^T]W_1=W_1^TCov(X)W_1=W_1^TSW_1,S=Cov(X)\)

• 接下来是最大化\(Var(Z_1)\),存在Constraint:\(|W_1|=1,W_1.TW_1-1=0\),利用拉格朗日算子法
  
  \(g(W_1)=W_1^TSW_1-\alpha(W_1.TW_1-1)\)
  
  \(\forall i<=m, \frac{\partial g(W_1)}{\partial W_{1i}}=0\rightarrow SW_1-\alpha W_1=0\) 可知\(W_1\)是S的特征向量，\(\alpha\)是S的特征值
  
  \(Var(Z_1)=W_1^TSW_1=W_1^T\alpha W_1=\alpha W_1^TW_1=\alpha\)，要是方差最大则\(\alpha\)是S的最大特征值，\(W_1\)为所对应的特征向量。

• 按照相同的思路来最大化\(Var(Z_2)\),存在constraints:\(W_2^TW_2-1=0,W_1^TW_2=0\)
  
  \(g(W_2)=W_2^TSW_2-\alpha(W_2^TW_2-1)-\beta(W_2^TW_1)\)
  
  \(\forall i<=m, \frac{\partial g(W_2)}{\partial W_{2i}}=0\)
  
  \(\rightarrow SW_2-\alpha W_2-\beta W_1=0 \rightarrow W_1^TSW_2-\alpha W_1^TW_2-\beta W_1^TW_1=0\)
  
  \(\rightarrow \beta=W_1^TSW_2=(W_1^TSW_2)^T=W_2^TSW_1=W_2^T\lambda W_1=\lambda W_2^TW_1=0\)
  
  因为\(\beta=0\)所以\(SW_2=\alpha W_2\),同理可知\(W_1\)是S的特征向量，\(\alpha\)是S的特征值
  
  \(Var(Z_2)=W_2^TSW_2=\alpha\),要想方差最大且满足约束条件(隐含条件S是Symmetric的，特征向量是正交的)，则\(\alpha\)是第二大的特征值且\(W_2\)是对应的特征向量。

• 第三步 得出结论
  
  降至不同空间维度上保存的信息量的大小是降维所用S的特征向量所对应的特征值的大小决定的

Conclusions

1、因为S一定是实对称矩阵，则经过对S的奇异值分解以后\(S=Q\sum Q^T\),\(\sum\)是一个对角线为S的特征值的矩阵,Q是特征值对应的特征列向量矩阵，从Q中抽取特征值最大的对应的特征列向量就可以进行降维,并且通过特征值算出简单的信息损失情况。

import numpy as np
U,S,V=np.linalg.svd(S)

人生此处，绝对乐观