正规表达式与有限自动机和LEX

正规式与有限自动机的等价性

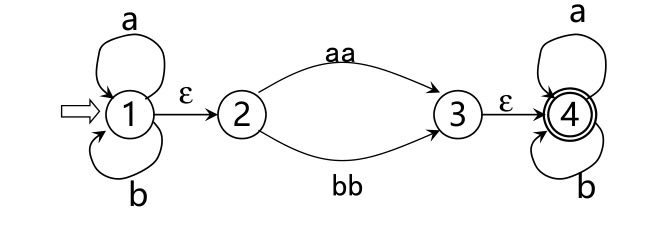
一个正规式r与一个有限自动机M等价， L(r)=L(M)

FA ->正规式，对任何FA M，都存在一个正规式r，使得L(r)=L(M)。

正规式 -> FA， 对任何正规式r，都存在一个FA M，使得L(M)=L(r)

为NFA构造正规式

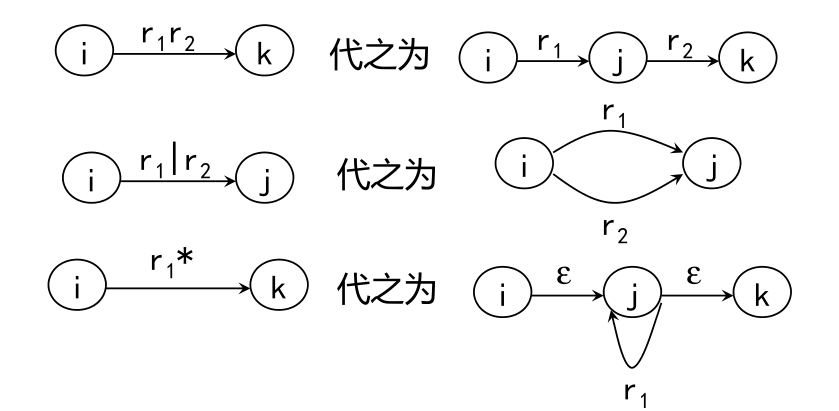
对转换图概念拓广，令每条弧可用一个正规式作标记，对Σ上任一NFA M，都存在一个Σ上的正规式r，使得L(r)=L(M)

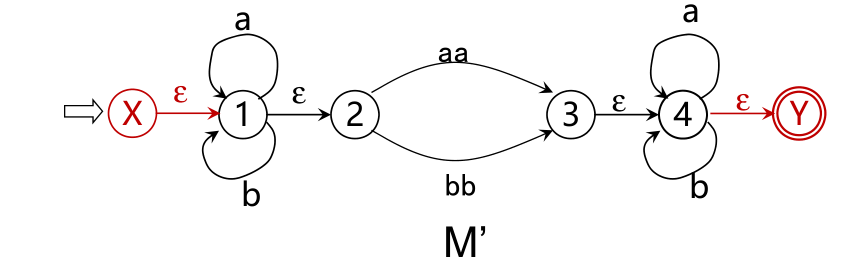
假定NFA M=<S, Σ, δ, S 0 , F>，我们对M的状态转换图进行以下改造：

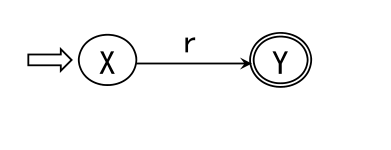
在M的转换图上加进两个状态X和Y，从X用ε弧连接到M的所有初态结点，从M的所有终态结点用ε弧连接到Y，从而形成一个新的NFA，记为M’，它只有一个初态X和一个终态Y，显然L(M)=L(M’)。

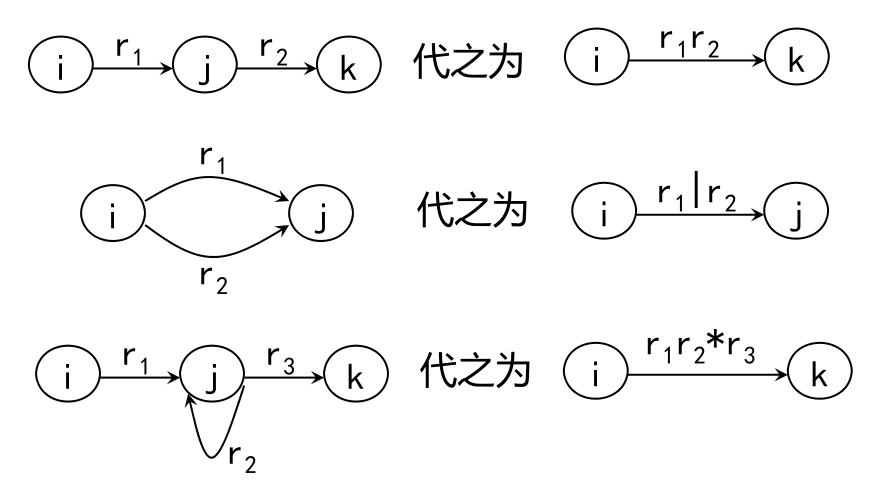
然后，反复使用下面的三条规则，逐步消去结点，直到只剩下X和Y为止。

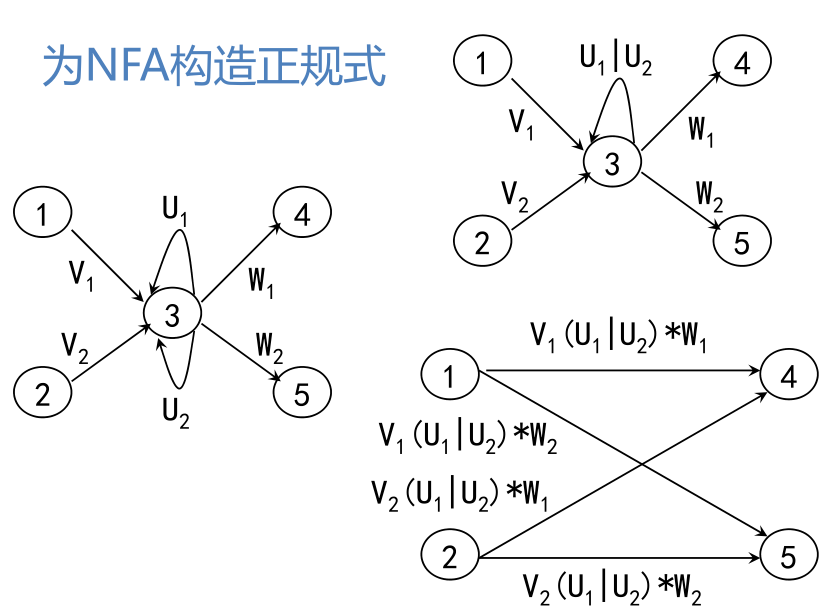
最后，X到Y的弧上标记的正规式即为所构造的正规式r

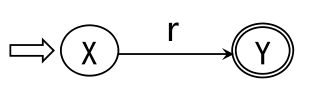
显然L(r)=L(M’)=L(M)，得证： 对Σ上任一NFA M，都存在一个Σ上的正规式r，使得L(r)=L(M)

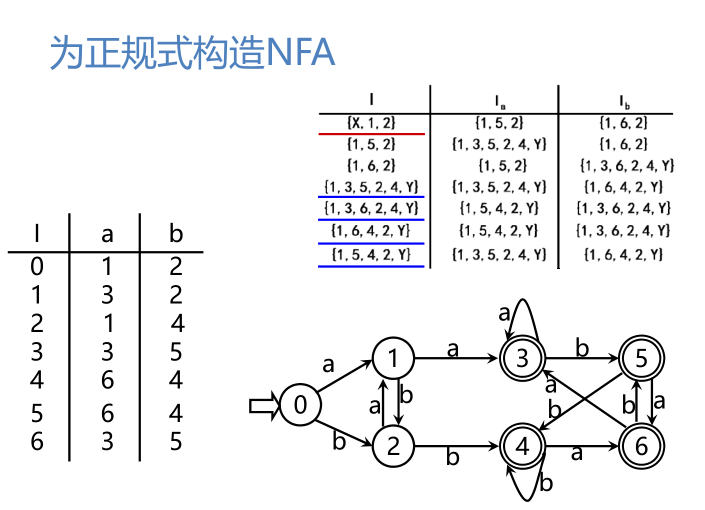
为正规式构造NFA

定理：对任何正规式r，都存在一个FA M，使得L(M)=L(r)

定理: 对于Σ上的正规式r，都存在一个NFA M，使L(M)=L(r)，并且M只有一个初态和一个终态，而且没有从终态出发的箭弧

对给定正规式r中的运算符数目进行归纳：

• 验证r中的运算符数目为0时，结论成立
• 假设结论对于运算符数目少于k(k≥1)的正规式成立
• 基于该假设，证明结论对于运算符数目为k的正规式成立

若r具有零个运算符，则r=ε或r=φ或r=a，其中a∈Σ

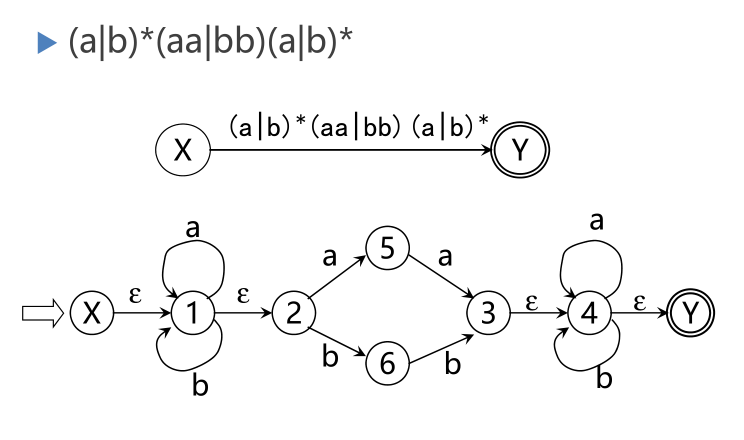
针对上述3类正规式r，分别按照下图构造NFAM，M只有一个初态和一个终态，而且没有从终态出发的箭弧，而且使L(M)和对应的L(r)相等。

假设对于运算符数目少于k(k≥1)的正规式成立

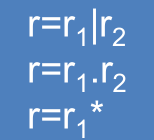
当r中含有k个运算符时，r有三种情形：

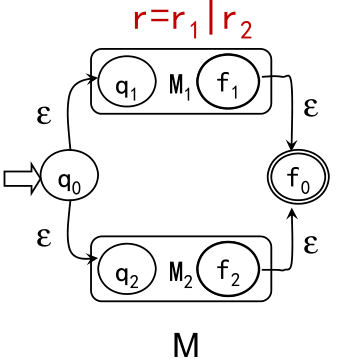
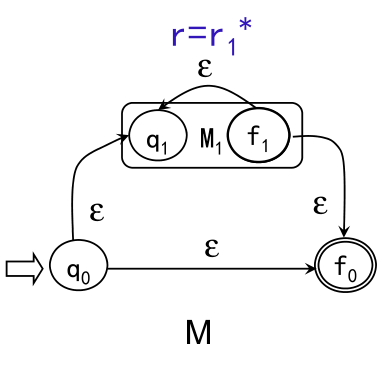
上述过程实质上是一个将正规表达式转换为有限自动机的算法

构造Σ上的NFA M’ 使得 L(r)=L(M’)，首先，把r表示成

按下面的三条规则对r进行分裂

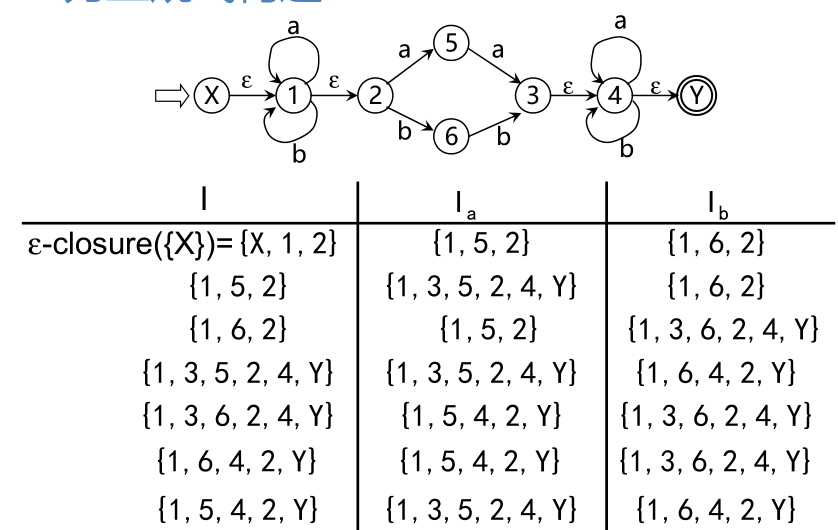
逐步把这个图转变为每条弧只标记为Σ上的一个字符或ε，最后得到一个NFA M’，显然L(M’)=L(r)

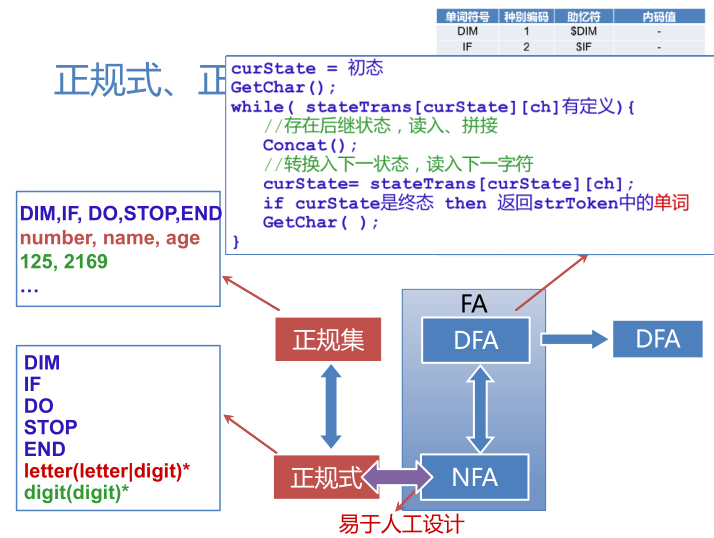
词法分析器的自动产生--LEX

LEX的工作过程

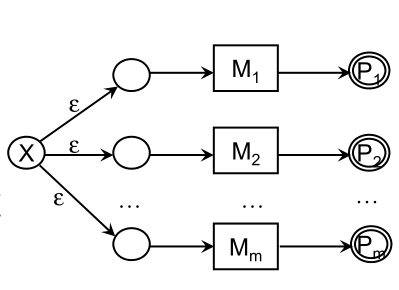
• 对每条识别规则P i 构造一个相应的非确定有限自动机M i ；
• 引进一个新初态X，通过ε弧，将这些自动机连接成一个新的NFA；
• 把M确定化、最小化，生成该DFA的状态转换表和控制执行程序