MLE
独立同分布的采样x1,x2,…,xn,θ为模型参数,f为我们所使用的模型。参数为θ的模型f产生上述采样可表示为
f(x1,x2,…,xn|θ)=πf(xi|θ)
已知的为x1,x2,…,xn,未知为θ,故似然定义为:L(θ|x1,x2,…,xn)=f(x1,x2,…,xn|θ)=πf(xi|θ)
常用的是两边取对数,得到公式如下:
lnL(θ|x1,x2,…,xn)=Σlnf(xi|θ)
其中lnL(θ|x1,x2,…,xn)称为对数似然,
而
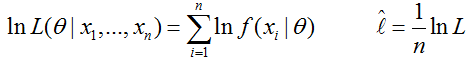
称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:
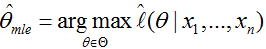
MLE的更多相关文章
- 萌新笔记——Cardinality Estimation算法学习(二)(Linear Counting算法、最大似然估计(MLE))
在上篇,我了解了基数的基本概念,现在进入Linear Counting算法的学习. 理解颇浅,还请大神指点! http://blog.codinglabs.org/articles/algorithm ...
- 最大似然估计 (MLE) 最大后验概率(MAP)
1) 最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即"模型已定,参数未知". 例如,我们知道这个分布是正态分布 ...
- 最大似然估计(MLE)与最小二乘估计(LSE)的区别
最大似然估计与最小二乘估计的区别 标签(空格分隔): 概率论与数理统计 最小二乘估计 对于最小二乘估计来说,最合理的参数估计量应该使得模型能最好地拟合样本数据,也就是估计值与观测值之差的平方和最小. ...
- 最大似然估计(MLE)和最大后验概率(MAP)
最大似然估计: 最大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”.简单而言,假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知 ...
- MLE MAP EM
1.最大似然估计 (MLE): 什么是最大似然估计? 问题:给定一组观察数据还有一个参数待定的模型,如何来估计这个未知参数呢? 观察数据(x1,y1)......(xn,yn) 待定模型 ...
- python sklearn PCA源码阅读:参数n_components的设置(设为‘mle’出错的原因)
在介绍n_components参数之前,首先贴一篇PCA参数详解的文章:http://www.cnblogs.com/akrusher/articles/6442549.html. 按照文章中对于n_ ...
- 参数估计:最大似然估计MLE
http://blog.csdn.net/pipisorry/article/details/51461997 最大似然估计MLE 顾名思义,当然是要找到一个参数,使得L最大,为什么要使得它最大呢,因 ...
- 频率学派与贝叶斯学派(先验分布与后验分布,MLE和MAP)
频率学派(古典学派)和贝叶斯学派是数理统计领域的两大流派. 这两大流派对世界的认知有本质的不同:频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范 ...
- 详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
转载声明:本文为转载文章,发表于nebulaf91的csdn博客.欢迎转载,但请务必保留本信息,注明文章出处. 原文作者: nebulaf91 原文原始地址:http://blog.csdn.net/ ...
- 补充资料——自己实现极大似然估计(最大似然估计)MLE
这篇文章给了我一个启发,我们可以自己用已知分布的密度函数进行组合,然后构建一个新的密度函数啦,然后用极大似然估计MLE进行估计. 代码和结果演示 代码: #取出MASS包这中的数据 data(geys ...
随机推荐
- [CTSC2010]珠宝商 SAM+后缀树+点分治
[CTSC2010]珠宝商 不错的题目 看似无法做,n<=5e4,8s,根号算法? 暴力一: n^2,+SAM上找匹配点的right集合sz,失配了直接退出 暴力二: O(m) 统计过lca=x ...
- JS时间戳转换成时间格式
TimeNow: function (val) { var date = new Date(val); var Y = date.getFullYear(); var m = date.getMont ...
- 【洛谷P4144】大河的序列
题目大意:给定一个长度为 N 的序列,求序列中连续区间最大的(或和加与和)是多少. 题解: 引理:任意两个数 \(i, j\),若 \(i>j\),则在二进制表示下,i 对应的二进制串的字典序一 ...
- tfs 2013 利用 web deploy 完成asp.net站点自动发布
课题起因: 目前我们团队使用visual studio 2013开发asp.net项目, 使用tfs2013 做源码管理, 每天早上手动发布项目文件包,复制到测试服务器的站点文件夹下覆盖老文件,用此方 ...
- mybatis的一些小知识
<update id="setReaded"> update wa_ent_job_app set IS_READ= 1, READ_TIME=now() where ...
- 谈.Net委托与线程——创建无阻塞的异步调用(一)
前言 本文大部分内容来自于mikeperetz的Asynchronous Method Invocation及本人的一些个人体会所得,希望对你有所帮助.原英文文献可以在codeproject中搜索到. ...
- day-04(jquery)
回顾: js: 组成部分: ECMAScript BOM DOM 变量声明 var 变量名=初始化值; 数据类型: 原始类型 Undefined Null String Number Boolean: ...
- Vue.js 循环语句
循环使用 v-for 指令. v-for 指令需要以 site in sites 形式的特殊语法, sites 是源数据数组并且 site 是数组元素迭代的别名. v-for 指令: v-for 可以 ...
- M1-day08-数据库加锁
一.关于数据库加锁主要分为几类 1.原生sql 1.开启事物 begin; select * from host for update; commit; 注意:INNODB支持表锁和行锁,MyISAM ...
- Linux基础入门教程
Linux基础入门教程 --------- Linux学习路径 Linux学习者,常常不知道自己改怎么学习linux:Linux初级,也就是入门linux前提是需要有一些计算机硬件相关的知识或是有一下 ...
