logistics回归理解

多元回归方程：假设有一个因变量y和一组自变量x₁, x₂, x₃, ... , x_n，其中y为连续变量，我们可以拟合一个线性方程：

y =β₀ +β₁*x₁ +β₂*x₂ +β₃*x₃ +...+β_n*x_n

如果y为二分类变量，只能取值0或1，那么线性回归方程就会遇到困难: 方程右侧是一个连续的值，取值为负无穷到正无穷，而左侧只能取值[0,1]，无法对应。为了继续使用线性回归的思想，统计学家想到了一个变换方法，就是将方程右边的取值变换为[0,1]。最后选中了Logistic函数：逻辑回归，可以说是在线性回归的基础上加上一个sigmoid函数，将线性回归产生的值归一化到[0-1]区间内。sigmoid函数如下：

y = 1 / (1+e^-x)

这是一个S型函数，值域为(0,1)，能将任何数值映射到(0,1)，且具有无限阶可导等优良数学性质。

我们将线性回归方程改写为：

y = 1 / (1+e^-z),

其中，z =β₀ +β₁*x₁ +β₂*x₂ +β₃*x₃ +...+β_n*x_n

此时方程两边的取值都在0和1之间。

进一步数学变换，也就是可以写为：

Ln(y/(1-y)) =β₀ +β₁*x₁ +β₂*x₂ +β₃*x₃ +...+β_n*x_n

Ln(y/(1-y))称为Logit变换。我们再将y视为y取值为1的概率p(y=1)，因此，1-y就是y取值为0的概率p(y=0)，所以上式改写为：

p(y=1) = e^z/(1+e^z),

p(y=0) = 1/(1+e^z),

其中，z =β₀ +β₁*x₁ +β₂*x₂ +β₃*x₃ +...+β_n*x_n.

（你看吼，你需要估计某件事发生的概率，这时候你有大量的训练样本，所以你想用一个多元回归来估计这个事儿，但是你多元回归所算出来的值特别多，而你的概率只处于0和1之间，这时候吧你就需要logistics了，）

接下来就可以使用”最大似然法”估计出各个系数β。

本文基本借鉴：http://blog.sina.com.cn/s/blog_44befaf60102vznn.html

这个出自：http://blog.csdn.net/YoYoDelphine/article/details/52888276

（你看吼，你所估计的跟真实值肯定有出入吧，这时候就需要找最优化的各个系数β吧，那你怎么找呢，就需要一个代价函数，代价函数分很多，求参有多种方法。比如最小二乘，比如最大然，比如交叉熵，这里用极大然是为了使这件事发生的概率最大化，也就是已知x，求β）

所谓参数估计就是：对未知参数θ进行估计时，在参数可能的取值范围内选取，使“样本获得此观测值x1,x2...,xn”的概率最大的参数θ^作为θ的估计，这样选定的θ^有利于x1,x2...,xn”的出现。也就是说在已知数据集（结果）和模型（分布函数）的情况下，估计出最适合该模型的参数。

举个例子：

假设你有一枚硬币，随机抛10次；现在的结果是6次正面。我们都知道，抛一枚硬币，正面朝上和反面朝上的概率均是θ=0.5；但前提时，这是在大量的实验（抛硬币）情况下才有的结论。那在我们这个情况下，参数θ到底取何值时才能使得出现6次正面的肯能性最大呢？

详情参见：http://blog.csdn.net/The_lastest/article/details/78761577

也就是n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）：

那最大似然法就是求模型中使得似然函数最大的系数取值θ*。这个最大似然就是我们的代价函数（cost function）了。

(截自李航《统计学习方法》)

（你看吼，这时候带代价函数，这里的代价函数就是这个事儿所有属性发生的概率*不发生的概率，就需要求β，然后需要用到梯度下降法对于每次的β迭代，也就是求导，对于极大似然函数求导，导数的方向也就是最好的下降方向 ，然后我们令该导数为0，你会很失望的发现，它无法解析求解。不信你就去尝试一下。所以没办法了，只能借助高大上的迭代来搞定了。这里选用了经典的梯度下降算法。

）

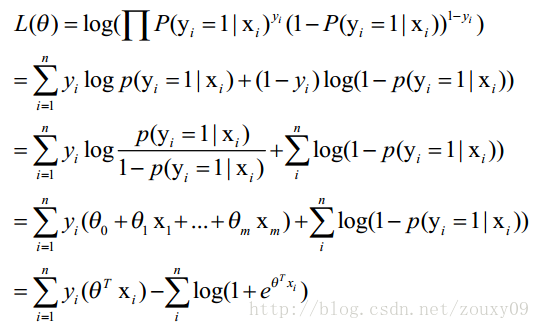
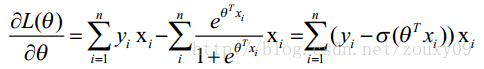
（θ求完导之后发现是θ=θ1+步长*（错误率）*本来的xi，下面就是优化了，在样本容量非常大的时候，你要随机选则，节省时间，然后就是逐步减小步长，这个在牛顿法中可以理解，迭代次数越高，越合适）

代码参考:http://blog.csdn.net/zouxy09/article/details/20319673

本文仅作作者笔记，没有任何冒犯的意思。。。