Floyd最短路(带路径输出)

摘要(以下内容来自百度)

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。

该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

简介编辑

在计算机科学中，Floyd-Warshall算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度（加权）。 虽然它不返回路径本身的细节，但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包，或（与Schulze投票系统相关）在加权图中所有顶点对之间的最宽路径。

Floyd-Warshall算法是动态规划的一个例子，并在1962年由Robert Floyd以其当前公认的形式出版。然而，它基本上与Bernard Roy在1959年先前发表的算法和1962年的Stephen Warshall中找到图形的传递闭包基本相同，并且与Kleene的算法密切相关 在1956年）用于将确定性有限自动机转换为正则表达式。算法作为三个嵌套for循环的现代公式首先由Peter Ingerman在1962年描述。

该算法也称为Floyd算法，Roy-Warshall算法，Roy-Floyd算法或WFI算法。 [2]

核心思路编辑

路径矩阵

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。 [3]

从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。

采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);

状态转移方程

其状态转移方程如下： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}；

map[i,j]表示i到j的最短距离，K是穷举i,j的断点，map[n,n]初值应该为0，或者按照题目意思来做。

当然，如果这条路没有通的话，还必须特殊处理，比如没有map[i,k]这条路。

算法过程编辑

1，从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。

2，对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。

把图用邻接矩阵G表示出来，如果从Vi到Vj有路可达，则G[i][j]=d，d表示该路的长度；否则G[i][j]=无穷大。定义一个矩阵D用来记录所插入点的信息，D[i][j]表示从Vi到Vj需要经过的点，初始化D[i][j]=j。把各个顶点插入图中，比较插点后的距离与原来的距离，G[i][j] = min( G[i][j], G[i][k]+G[k][j] )，如果G[i][j]的值变小，则D[i][j]=k。在G中包含有两点之间最短道路的信息，而在D中则包含了最短通路径的信息。

比如，要寻找从V5到V1的路径。根据D，假如D(5,1)=3则说明从V5到V1经过V3，路径为{V5,V3,V1}，如果D(5,3)=3，说明V5与V3直接相连，如果D(3,1)=1，说明V3与V1直接相连。 [4]

时间复杂度与空间复杂度编辑

时间复杂度:O(n^3)；

空间复杂度:O(n^2)

优缺点分析编辑

Floyd算法适用于APSP(All Pairs Shortest Paths，多源最短路径)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法，也要高于执行|V|次SPFA算法。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

缺点：时间复杂度比较高，不适合计算大量数据。 [5]

关键的路径输出

例如

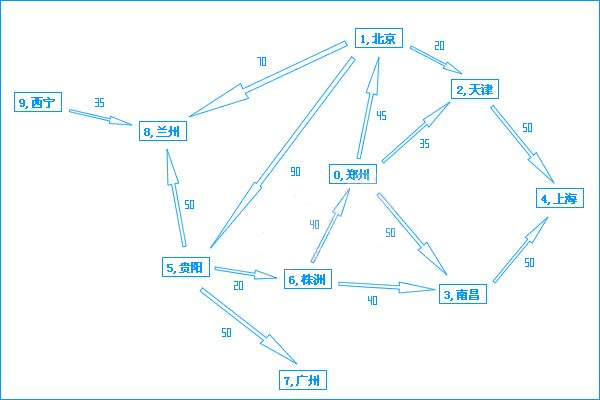
具体看代码

代码

#include<bits/stdc++.h>
using namespace std;
const int inf=999999;
int mp[20][20],path[20][20];
int n,m;
void print(int a,int b){
	if(path[a][b]==-1) return;//因为开始初始化为-1，这里就可以避免相邻的再次输出
	print(a,path[a][b]);//前半部
	cout<<path[a][b]<<"-->";//输出该点
	print(path[a][b],b);//后半部
}
int main(){
 // freopen("in.txt","r",stdin);
  while(cin>>n>>m){
  	memset(path,-1,sizeof(path));//初始化-1
    for(int i=0;i<n;i++)
    for(int j=0;j<n;j++) if(i==j) mp[i][j]=0;
     else mp[i][j]=inf;
   int Start,End,dis;
  for(int i=0;i<m;i++)
     {
     	cin>>Start>>End>>dis;
     	mp[Start][End]=dis;
 }
 //三层循环
 for(int k=0;k<n;k++)
 {
 	//第k个点进行松弛
 	for(int i=0;i<n;i++)
 	for(int j=0;j<n;j++)
 	if(mp[i][j]>mp[i][k]+mp[k][j])//如果能够缩短就更新距离
 	{
 		mp[i][j]=mp[i][k]+mp[k][j];
 		path[i][j]=k;//记录能松弛的点
	 }
  }
 cout<<"The shortest path between vertices\n";
 for(int i=0;i<n;i++)
 for(int j=0;j<n;j++)
 {
 	if(mp[i][j]==inf){//两者不通
 		cout<<i<<' '<<j;
 		cout<<" These two points cannot be reached\n\n"; continue;
	 }
 	cout<<i<<" to "<<j<<" shortest path is "<<mp[i][j]<<endl;
 	cout<<"The specific path is\n";
 	cout<<i<<"-->";
 	print(i,j);
 	cout<<j<<' ';
 	cout<<endl<<endl;
 }
}
return 0;
}
//输入数据
/*
10 14
0 1 45
0 2 35
0 3 50
1 2 20
1 5 90
1 8 70
2 4 50
3 4 50
5 6 20
5 7 50
5 8 50
6 0 40
6 3 40
9 8 35
*/