数学模型：3.非监督学习--聚类分析 和K-means聚类

1. 聚类分析

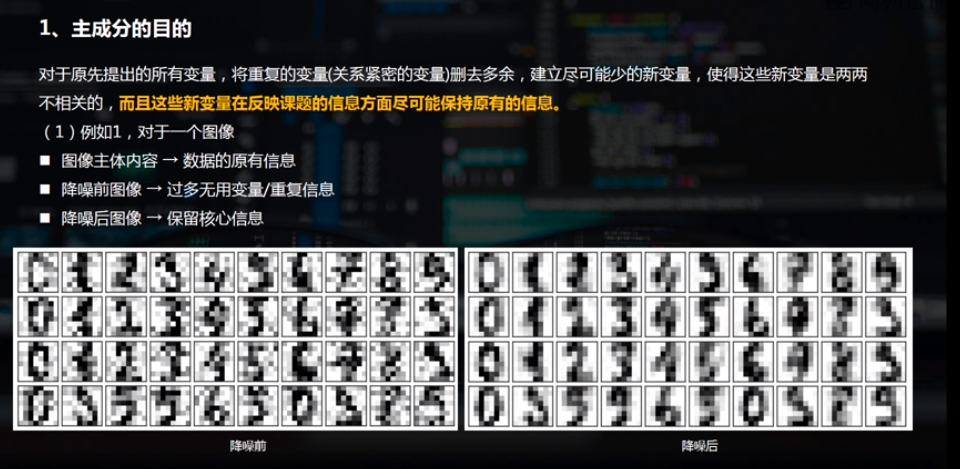
聚类分析（cluster analysis）是一组将研究对象分为相对同质的群组（clusters）的统计分析技术 ---->>

将观测对象的群体按照相似性和相异性进行不同群组的划分，划分后每个群组内部各对象相似度很高，而不同群组之间的对象彼此相异度很高。

*** 回归、分类、聚类的区别 ：

　　有监督学习 --->> 回归，分类    /   无监督学习  --->>聚类

　　回归 -->>产生连续结果，可用于预测

　　分类 -->>产生连续结果，可用于预测

　　聚类 -->>产生一组集合，可用于降维。

本文主要介绍PCA主成分，K-means聚类

1.1 PCA主成分分析

1.2 PCA主成分的python实现方法

PCA主成分分析的python实现方法

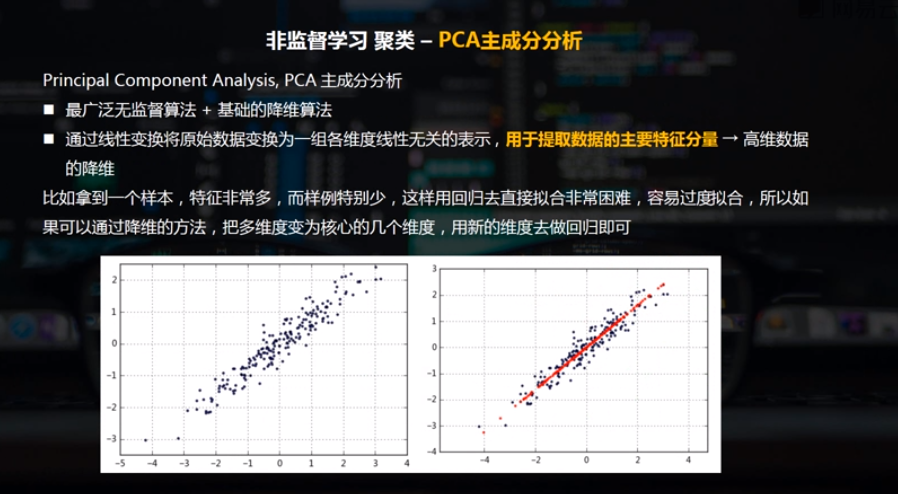
最广泛无监督算法 + 基础的降维算法
通过线性变换将原始数据变换为一组各维度线性无关的表示，用于提取数据的主要特征分量 → 高维数据的降维

二维数据降维 / 多维数据降维

（1）二维数据降维

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline

# 二维数据降维
# 数据创建
rng = np.random.RandomState(8)
data = np.dot(rng.rand(2,2),rng.randn(2,200)).T  #矩阵相乘的方法
df = pd.DataFrame({'X1':data[:,0],
                    'X2':data[:,1]})
print(df.head())
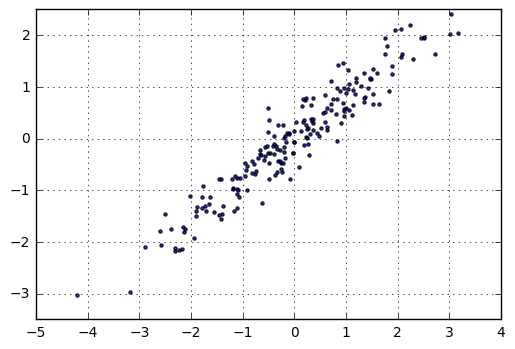
print(df.shape)
 
plt.scatter(df['X1'],df['X2'], alpha = 0.8, marker = '.')
plt.axis('equal')
plt.grid()
# 生成图表

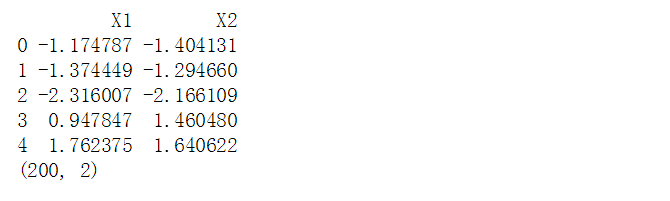
# 二维数据降维（二维降为一维只有1个特征值，2个特征向量）
# 构建模型，分析主成分
 
from sklearn.decomposition import PCA
# 加载主成分分析模块PCA
 
pca = PCA(n_components = 1)  # n_components = 1 → 降为1维
pca.fit(df)  # 构建模型
# sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
# n_components:  PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n
# copy: True或者False，默认为True → 表示是否在运行算法时，将原始训练数据复制一份
# fit(X,y=None) → 调用fit方法的对象本身。比如pca.fit(X)，表示用X对pca这个对象进行训练
print(pca.explained_variance_) #特征值       [ 2.78300591] -
print(pca.components_)#特征向量              [[ 0.7788006   0.62727158]]
print(pca.n_components) #主成分,成分的个数  1
#成分的结果值 = 2.78 * （0.77*x1 + 0.62 * x2） #通过这个来筛选它的主成分。
 
# components_：返回具有最大方差的成分。
# explained_variance_ratio_：返回 所保留的n个成分各自的方差百分比。
# n_components_：返回所保留的成分个数n。
 
# 这里是shape(200,2)降为shape(200,1)，只有1个特征值，对应2个特征向量
# 降维后主成分 A1 = 0.7788006 * X1 + 0.62727158 * X2
 
x_pca = pca.transform(df) #得到主成分A1的值；
x_pca
 
x_pca = pca.transform(df)  # 数据转换
x_new = pca.inverse_transform(x_pca)  # 将降维后的数据转换成原始数据的格式（二维的格式）
print('original shape:',df.shape)
print('transformed shape:',x_pca.shape)
print(x_pca[:5])
print('-----')
# 主成分分析，生成新的向量x_pca
# fit_transform(X) → 用X来训练PCA模型，同时返回降维后的数据，这里x_pca就是降维后的数据
# inverse_transform() → 将降维后的数据转换成原始数据

plt.scatter(df['X1'],df['X2'], alpha = 0.8, marker = '.') #原始数据的散点，黑点；
plt.scatter(x_new[:,0],x_new[:,1], alpha = 0.8, marker = '.',color = 'r') #转换之后的散点，红色的就是最后的特征数据
plt.axis('equal')
plt.grid()
# # 生成图表

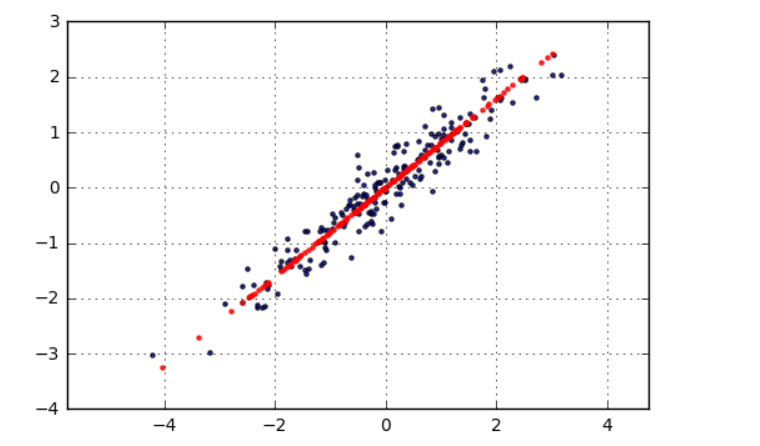
构建模型--输出维度--加载数据--特征向量、特征值--

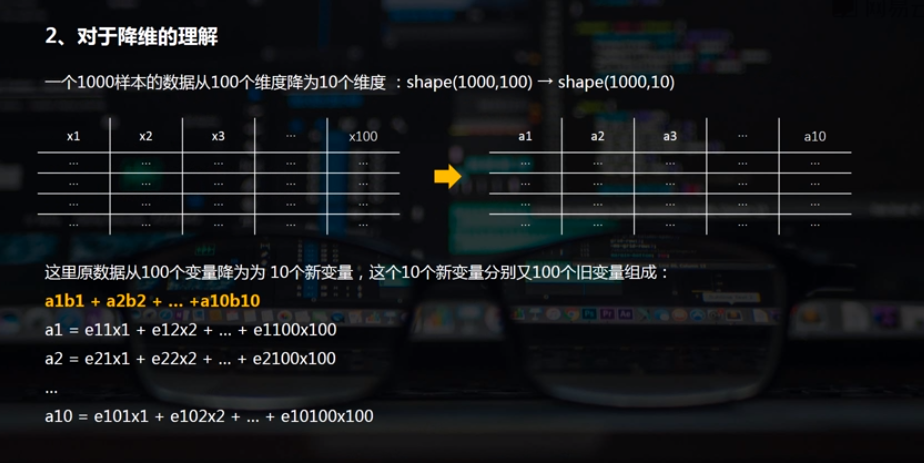
（2）多维数据降维

# 多维数据降维  加载数据，用的是图像的一个数据。
from sklearn.datasets import load_digits
digits = load_digits()
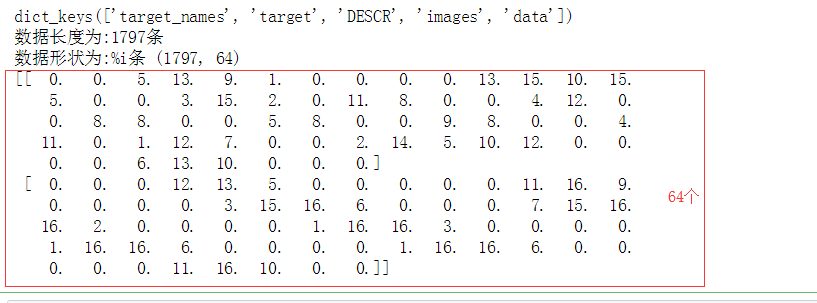
print(digits .keys())
print('数据长度为:%i条' % len(digits['data']))
print('数据形状为:%i条',digits.data.shape) #总共1797条数据，每条数据有64个变量
print(digits.data[:2])
# 导入数据

# 多维数据降维
# 构建模型，分析主成分
 
pca = PCA(n_components = 2)  # 降为2纬
projected = pca.fit_transform(digits.data)
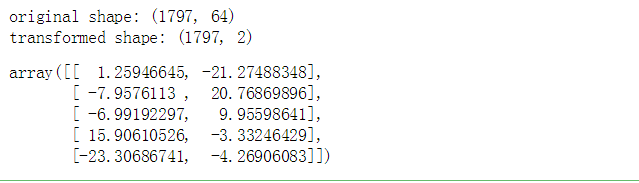
print('original shape:',digits.data.shape) #降维前
print('transformed shape:',projected.shape) #降维后的
projected[:5]

print(pca.explained_variance_)  # 输出特征值 ；降了2个维度 ，所以它的特征值只显178.9和163.6，贡献率算的话这两个肯定都属于主成分。
# print(pca.components_)  # 输出特征向量 ,64个特征向量  .shape是形状  ； 2个维度要把其中的64个都给算出来
#print(projected)  # 输出解析后数据
# 降维后，得到2个成分，每个成分有64个特征向量
 
plt.scatter(projected[:,0],projected[:,1],
           c = digits.target, edgecolor = 'none',alpha = 0.5,
           cmap = 'Reds',s = 5)
plt.axis('equal')
plt.grid()
plt.colorbar()
# 二维数据制图

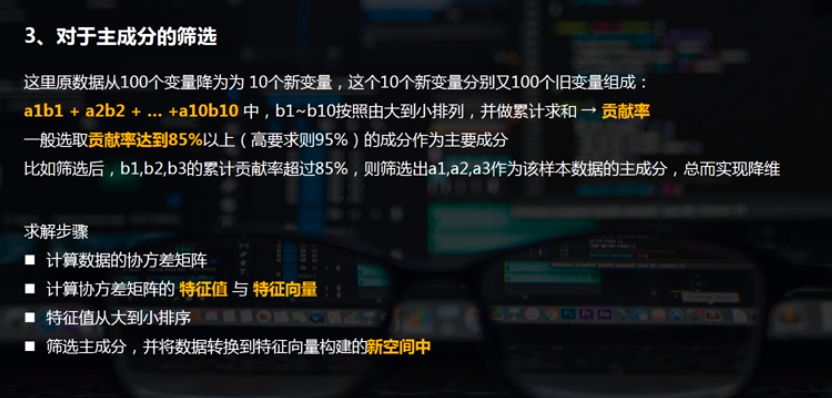
# 多维数据降维
# 主成分筛选
 
pca = PCA(n_components = 10)  # 降为10纬  
projected = pca.fit_transform(digits.data)
print('original shape:',digits.data.shape)
print('transformed shape:',projected.shape)
print(pca.explained_variance_)  # 输出特征值 ；10个特征值
print(pca.components_.shape)  # 输出特征向量形状
#print(projected)  # 输出解析后数据
# 降维后，得到10个成分，每个成分有64个特征向量
 
c_s = pd.DataFrame({'b':pca.explained_variance_,  #把所有特征值筛选出来看是否有主成分
                   'b_sum':pca.explained_variance_.cumsum()/pca.explained_variance_.sum()})
print(c_s)
# 做贡献率累计求和，再除以它的总和
# 可以看到第7个成分时候，贡献率超过85% → 选取前7个成分作为主成分

c_s['b_sum'].plot(style = '--ko', figsize = (10,4))
plt.axhline(0.85,hold=None,color='r',linestyle="--",alpha=0.8)
plt.text(6,c_s['b_sum'].iloc[6]-0.08,'第7个成分累计贡献率超过85%',color = 'r')
plt.grid()

3. K-means聚类的python实现方法

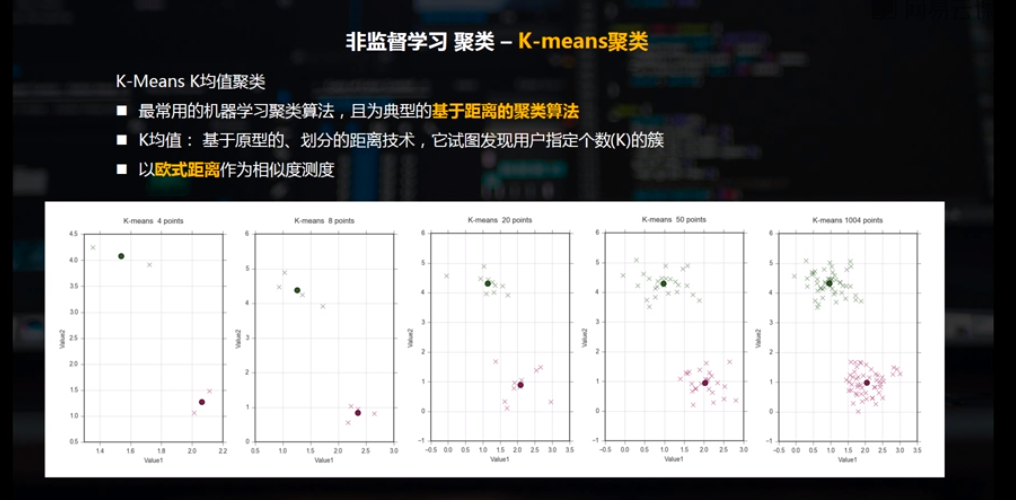
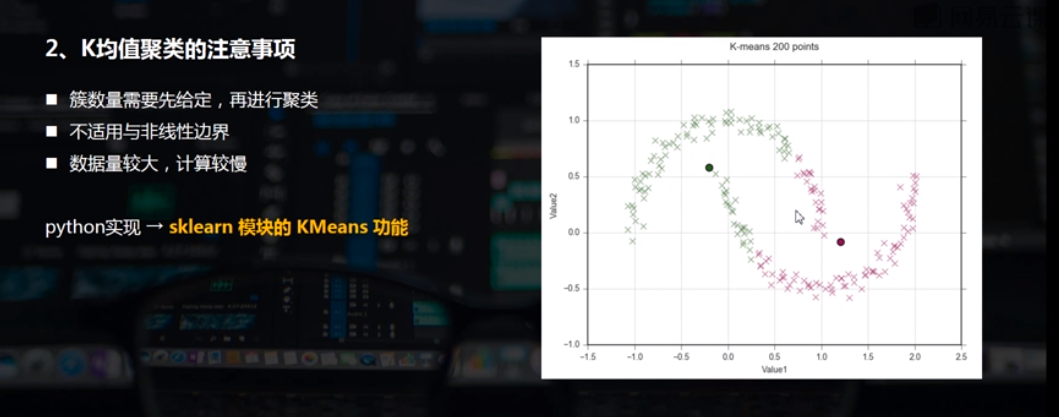
最常用的机器学习聚类算法，且为典型的基于距离的聚类算法
K均值： 基于原型的、划分的距离技术，它试图发现用户指定个数(K)的簇
以欧式距离作为相似度测度

# 创建数据
 
from sklearn.datasets.samples_generator import make_blobs
# make_blobs聚类数据生成器
 
x,y_true = make_blobs(n_samples = 300,   # 生成300条数据
                     centers = 4,        # 四类数据
                     cluster_std = 0.5,  # 方差一致，越小聚集越小，越大越分散；也可以分散地写 [0.2,0.2,0.3,0.5],
                     random_state = 0)
print(x[:5])
print(y_true[:5])
# n_samples → 待生成的样本的总数。
# n_features → 每个样本的特征数。
# centers → 类别数
# cluster_std → 每个类别的方差，如多类数据不同方差，可设置为[1.0,3.0]（这里针对2类数据）
# random_state → 随机数种子
# x → 生成数据值， y → 生成数据对应的类别标签
 
plt.scatter(x[:,0],x[:,1],s = 10,alpha = 0.8)
plt.grid()
# 绘制图表

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters =)  #4个类别，这里写它一共有多少个簇；
kmeans.fit(x)  #加载构建数据
y_kmeans = kmeans.predict(x) #生成聚类之后的一个类别值，分好类的数据标签
centroids = kmeans.cluster_centers_  #生成4个类的中心点
# 构建模型，并预测出样本的类别y_kmeans
# kmeans.cluster_centers_：得到不同簇的中心点
 
plt.scatter(x[:, 0], x[:, 1], c = y_kmeans, cmap = 'Dark2', s = 50, alpha = 0.5, marker = 'x')
plt.scatter(x[:,0],x[:,1],c = y_kmeans, cmap = 'Dark2', s= 50,alpha = 0.5,marker='x')
plt.scatter(centroids[:,0],centroids[:,1],c = [0,1,2,3], cmap = 'Dark2',s= 70,marker='o')
plt.title('K-means 300 points\n')
plt.xlabel('Value1')
plt.ylabel('Value2')
plt.grid()
# 绘制图表
centroids